阶梯圆柱壳在轴向冲击载荷作用下的屈曲计算分析
2019-01-23桂夷斐马建敏
桂夷斐, 马建敏
(复旦大学 航空航天系,上海 200433)
目前,应用较为广泛的缓冲元件主要是薄壁构件,因其具有良好的吸能特性,在受到冲击载荷的作用时,破坏形式较为稳定,主要通过自身的塑性变形吸收和耗散能量,达到缓冲保护的目的。因此在许多工程领域,不同构型的圆柱壳被广泛使用。对用于结构防撞安全及各类塑性变形吸收装置的圆柱壳,其在冲击载荷作用下的动力屈曲一直是研究的热点问题之一。
60年代以来,许多学者对轴向冲击弹性圆柱壳的动态屈曲进行了研究,Ohira[1],Stein[2]以及Hoff[3]基于Donnell壳理论并忽略前屈曲,对于不同端部支承条件下的圆柱壳得到了很多精确解。Zimicik等[4]对径厚比为100~160的圆柱壳受轴向脉冲载荷作用下的弹塑性动力屈曲进行了理论和实验研究。王仁等[5]对厚壳做了大量的冲击实验发现了圆柱壳发生非对称屈曲的第二临界速度。陈永涛等[6-7]研究薄壁圆柱壳的动态屈曲模式,分析构造具有高吸能率的抗冲击结构的方法。顾红军等[8-9]对薄壁圆柱壳的轴向动力屈曲进行了实验与理论研究,了解了轴向冲击下薄壁圆柱壳的屈曲行为。黄承义等[10]采用Lagrange方法分析了有限长薄壁圆柱壳在余弦冲击载荷作用下的弹性脉冲动力屈曲。徐新生等[11-12]研究了半无限长弹性圆柱壳的屈曲机理,并发现轴向应力波的传播和反射对屈曲起着重要作用。Tovstik等[13]为了得到能预测不同端部支承条件下的临界载荷以及屈曲模态的近似表达式,采用渐进法进行了大量的屈曲分析。杨卫奇等[14]采用LS-DYNA对圆柱壳动力屈曲全过程进行了数值模拟,分析了屈曲行为及屈曲过程中的应力波效应。Karagiozova等[15-16]基于轴向冲击产生的应力波效应,研究了圆柱壳的动态塑性屈曲及动态渐进屈曲现象,并通过实验研究了冲击速度和材料特性对动态屈曲响应的影响。Xu等[17]考虑轴向应力波的传播和反射建立辛体系研究了在轴向冲击载荷下圆柱壳的局部屈曲。
本文在前人研究圆柱壳的基础上,通过改变壳的几何构型来讨论壳体在不同构型下缓冲吸能特性,因此提出了阶梯形壳的概念。阶梯形圆柱壳结构在工程实践中有着广泛的应用,例如激光平台的减震基座,火箭的燃料箱,各种动力机械中的阶梯形柱壳零件。研究在轴向阶跃载荷作用下应力波传播及反射对阶梯圆柱壳动力屈曲的影响,首先将阶梯圆柱壳拆分成两段圆柱壳(如图1所示,设与固定端直接相连半段为左半段,与固定端不直接相连半段为右半段)进行建模并求解,之后考虑应力波传播及反射在分界面处的连续性条件建立两段圆柱壳的联系,从而得到完整阶梯圆柱壳的控制方程及解的形式。最后考虑边界条件和应力波波阵面到达壳的不同位置的相容条件,求得相应的屈曲分叉条件。计算分析阶梯圆柱壳临界屈曲载荷与应力波波阵面、阶梯圆柱壳左半段的壁厚与中面半径比(以下简称厚径比)、阶梯圆柱壳右半段厚度与左半段厚度之比(以下简称厚度比)的关系;并且比较了质量相同的阶梯圆柱壳与等厚度圆柱壳发生屈曲的临界载荷。

图1 受轴向冲击的阶梯圆柱壳
1 控制方程及求解
如图1所示的阶梯圆柱壳,由两段长均为L,中面半径均为r的圆柱壳组成,其中左半段圆柱壳厚度h,右半段厚度为左半段的s倍。阶梯圆柱壳密度为ρ,弹性模量为E,泊松比为ν。建立柱坐标系,x,θ,z分别表示轴向、周向和径向坐标,w表示壳体中面上的点沿z轴方向的位移。根据弹性圆柱壳屈曲的哈密顿变分原理,建立左半段和右半段圆柱壳的径向位移控制方程[18]分别如式(1)和(2)所示
(1)
(2)
其中D=Eh3/12(1-ν2),Nx是壳体所受轴向载荷,壳体端部受轴向阶跃载荷冲击时,圆柱壳中应力波以纵波的形式传播,应力波传播波阵面位置xe,反射波波阵面位置xr,其中ce为波速。本文主要讨论阶梯圆柱壳受轴向冲击后,应力波从冲击端传播到固定端并经固定端反射回冲击端的情况,由于分界面对应力波传播产生反射和透射,阶梯圆柱壳被应力波波阵面划分成四个区域为Ⅰ、Ⅱ、Ⅲ、Ⅳ。对于理想弹性阶梯圆柱壳的应力波传播和反射可通过其轴向力被描述为
令
W=w/r,X=x/r,T=cet/r,ξ2=h2/3r2(1-ν2),
P=Nx/Eh,代入式(1)可将其无量纲化为如下形式
(3)
令
W(X,θ,T)=Φ(X,T)Ψ(θ,T)
(4)
考虑函数Ψ(θ,T)的边界连续条件(θ=0和θ=2π)有
(5)
由上式可以求出Ψ(θ,T)的通解为
Ψ(θ,T)=c1cos(ηθ)+c2sin(ηθ)
(6)
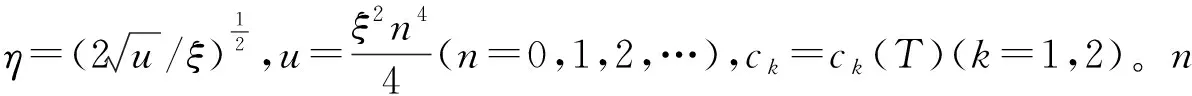
(7)
对于右半段经相同的处理方法得到关于Φ(X,T)满足的方程为
(8)
采用无量纲参数,阶梯圆柱壳总长为2,冲击端处X=0,分界面处X=1,固定端处X=2。求解式(7)和(8)可得到Φ(X,T)的通解为
(9)

(10)

(11)

(12)
其中


2 边界条件及相容条件
2.1 边界条件
考虑冲击端部铰支,非冲击端部固支有

(13)
(14)
2.2 相容条件
应力波传播经过固定端会发生反射,根据应力波反射到达不同的时间段,有如下相容条件
2.2.1 反射波波阵面到达区域Ⅲ与区域Ⅳ交界面

(15)
考虑分界面处的相容条件:
(16)
2.2.2 反射波波阵面到达区域Ⅰ与区域Ⅱ交界面

(17)
考虑分界面处的相容条件
(18)
3 分叉条件
阶梯圆柱壳分叉意味着在轴向阶跃载荷作用下壳体不能维持在平衡位置附近的微小横向振动而变成发散型运动的过程。接下来对应力波传播到达固定端发生反射后的屈曲分叉进行研究。

A3C3=0
(19)
其中C3=(a2,b2,c2,d2,a3,b3,c3,d3,a4,b4,c4,d4)T,得到A3为12×12矩阵,式中若C3=(a2,b2,c2,d2,a3,b3,c3,d3,a4,b4,c4,d4)T=0,由式(11)中Φ(X,T)表达式可知Φ(X,T)=0,则W(X,θ,T)=Φ(X,T)Ψ(θ,T)=0,说明屈曲现象将不发生。所以上式有非零解的条件即分叉条件是
|A3|=0
(20)

A4C4=0
(21)
其中
得到A4为12×12矩阵,有分叉条件
|A4|=0
(22)
4 数值计算结果及分析
冲击端部铰支,非冲击端部固支的阶梯圆柱壳受轴向阶跃载荷作用,发生屈曲的临界载荷可由分叉条件得到。分叉屈曲有多个分支,取前三阶的前三支曲线进行分析。
图2给出了将厚径比ξ=0.05,厚度比s=2代入式(20)和(22)得到的临界载荷随应力波波阵面的变化曲线。
从图2可以看出,随着屈曲阶数n的增大临界屈曲载荷值越大,n=0,即发生轴对称屈曲时临界载荷最小。应力波经固定端反射,反射波未通过分界面前临界载荷逐渐降低并趋于平缓;反射波通过分界面后临界屈曲载荷相对缓慢地下降。
图3(a)给出了将s=2,T=2.5(表示在时刻T,应力波波阵面到达阶梯圆柱壳某一位置,此处代表反射波未通过分界面)代入式(20)得到的临界载荷与厚径比的关系;图3(b)给出了将s=2,T=3.5(表示在时刻T,应力波波阵面到达阶梯圆柱壳某一位置,此处代表反射波通过了分界面)代入式(22)得到的临界载荷与厚径比的关系。
从图3可以看出,随着屈曲阶数n的增大临界屈曲载荷值越大,n=0,即发生轴对称屈曲时临界载荷最小。随着厚径比增大临界载荷也随之增大。
图4(a)给出了将ξ=0.05,T=2.5代入式(20)得到的临界载荷与厚度比的关系;图4(b)给出了将ξ=0.05,T=3.5代入式(22)得到的临界载荷与厚度比的关系。

(a) 波阵面到达区域Ⅲ与区域Ⅳ交界面

(b) 波阵面到达区域Ⅰ与区域Ⅱ交界面
Fig.2 The axial critical buckling loads with time of wave front propagation

(a) 波阵面到达区域Ⅲ与区域Ⅳ交界面

(b) 波阵面到达区域Ⅰ与区域Ⅱ交界面
Fig.3 The axial critical buckling loads with the ratio of thickness and radius
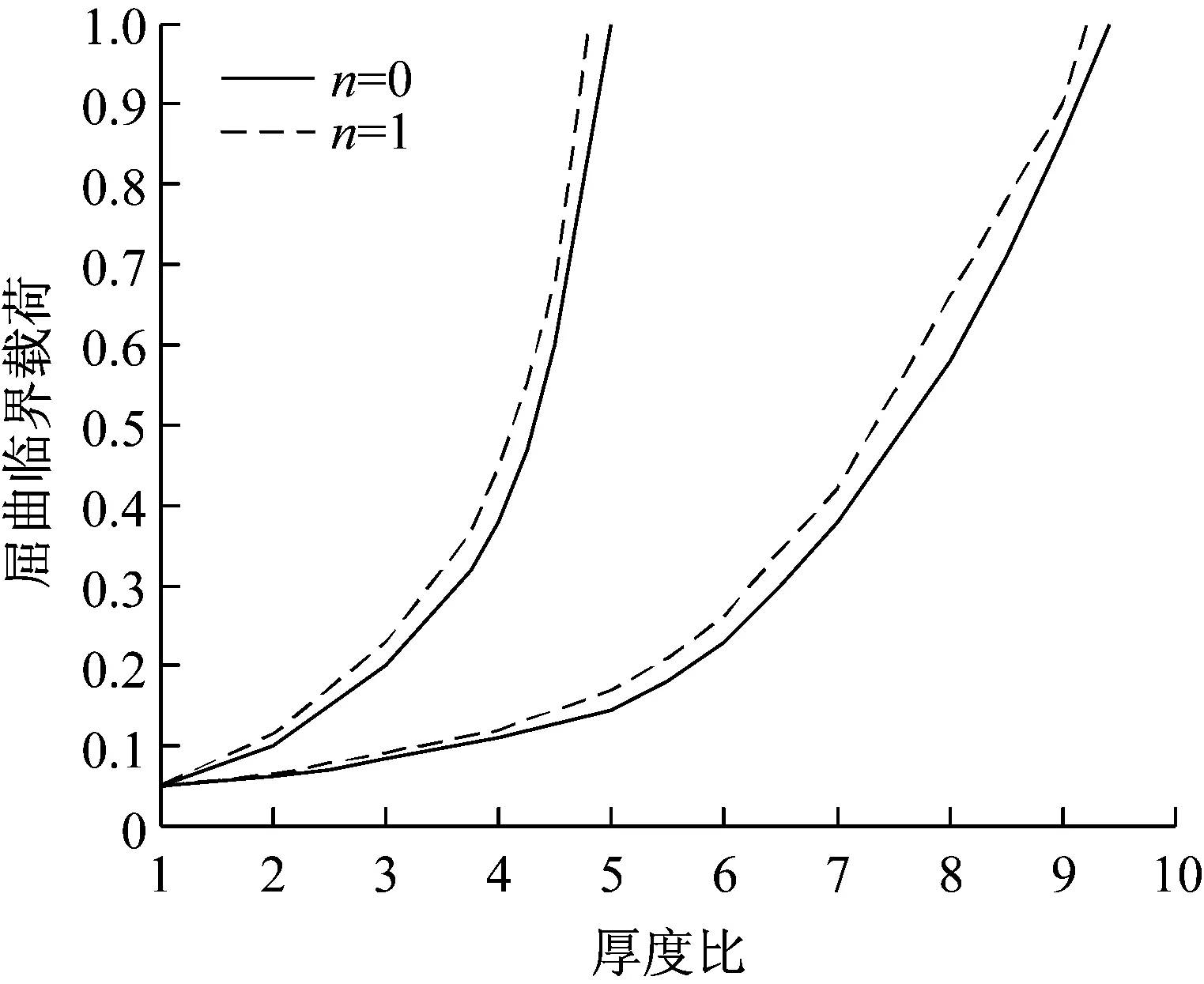
(a) 波阵面到达区域Ⅲ与区域Ⅳ交界面

(b) 波阵面到达区域Ⅰ与区域Ⅱ交界面
从图4可以看出,随着屈曲阶数n的增大临界屈曲载荷值越大,n=0,即发生轴对称屈曲时临界载荷最小。随着厚度比增大临界载荷也随之增大,应力波经固定端反射通过分界面之前临界载荷随厚度比增大曲线越来越陡;反射波通过分界面后临界载荷随厚度比增大相对平缓。
从图5可以看出,应力波经固定端反射通过分界面之前相同质量的阶梯圆柱壳比等厚度圆柱壳更易发生屈曲,且随着厚度比增大,屈曲越容易发生;反射波通过分界面后相同质量的阶梯圆柱壳比等厚度圆柱壳更难发生屈曲,且随着厚度比增大越难发生屈曲。
5 结 论
对于阶跃载荷作用的阶梯圆柱壳,考虑冲击端部为铰支,非冲击端部为固支的情况。计算分析了应力波经固定端发生反射后,阶梯圆柱壳临界屈曲载荷分别与波阵面传播位置,厚径比,厚度比的关系;并比较了阶梯圆柱壳与等厚度圆柱壳的屈曲临界载荷。计算结果表明:

(a) 波阵面到达区域Ⅲ与区域Ⅳ交界面

(b) 波阵面到达区域Ⅰ与区域Ⅱ交界面
Fig.5 The comparison of the critical buckling loads about const-ant thickness and step cylindrical shells
(1) 发生非轴对称屈曲比轴对称屈曲的临界载荷大。
(2) 应力波传播经固定端反射,反射波通过分界面后比通过分界面之前固定端部更难发生屈曲,而冲击端部较易发生屈曲。
(3) 随着厚径比增大临界载荷也随之增大,且阶数越高的临界载荷越大。
(4) 应力波经固定端反射通过分界面之前临界屈曲载荷随厚度比增大快速增大;反射波通过分界面后临界载荷随厚度比增大增长比较平缓。
(5) 应力波经固定端反射通过分界面之前相同质量的阶梯圆柱壳比等厚度圆柱壳更易发生屈曲,反射波通过分界面后相同质量的阶梯圆柱壳比等厚度圆柱壳更难发生屈曲。
