基于改进反向差分进化算法的多股簧响应模型参数辨识

丁传俊， 张相炎， 刘 宁

(南京理工大学 机械工程学院，南京 210094)

多股螺旋弹簧(简称多股簧)是由多股钢丝拧成钢索卷制而成的圆柱螺旋弹簧(见图1)。和普通单股弹簧相比，多股簧抗冲击性能好、吸振能力强、具有较大的刚度和非线性阻尼、寿命长，常被用作小口径自动武器的缓冲复进簧。

由于构成弹簧的各股钢丝之间存在着复杂的接触(挤压)和摩擦，多股簧在加载过程中具有明显的非线性刚度和迟滞特性。为描述这两种复杂的特性，王时龙等[1]和闵建军等[2]分别建立了多股簧的静态分段折线模型，但刚度上的突变难以真实地反映系统的加载和卸载特性；Zhao等[3]提出了多股簧的动态修正Bouc-Wen模型，该模型作为光滑曲线模型，认为恢复力不仅与加载位移有关，还与加载路径有关。由于光滑曲线模型的恢复力与相对位移的光滑过渡关系比较符合实际，通过选择适当的模型参数可以构造出不同能耗、渐硬或渐软特性的迟滞模型，因此适合于多股簧建模。

Bouc-Wen模型及其修正模型的参数识别问题可以归结为优化问题，即通过定义一个关于系统模型的成本函数，利用优化方法来识别多股簧响应模型的参数。但传统的优化方法往往需要设定合适的初始值，或者需要计算成本函数的海森矩阵，因此限制了这类方法的应用，而基于种群进化的差分进化算法(Differential Evolution, DE)[4-5]可以很好地弥补经典优化方法的不足，进而受到了广泛的关注，具体的应用情况可以参考文献[6-7]。

图1 多股螺旋弹簧

近些年来，基于反向学习(Opposition-based Learning, OBL)的差分进化算法(ODE)[8]及其改进算法因具有较好的收敛速度和精度而受到广泛的关注和研究。理论和试验已经证明通过同时考虑当前解及其反向解可以有效地使种群向全局最优空间逼近。其中，Wang等[9]通过对求解边界进行随机扰动，提出了广义反向算法(GODE)并论证了算法收敛性；通过论证准反向点、普通反向点与全局最优解的距离，Rahnamayan等[10]提出了准反向差分进化算法(QODE)；基于QODE，Ergezer等[11]提出了准反射反向差分进化算法(QRODE)；考虑到多数优化问题的最优解并不位于求解区域的中心，Xu等[12]提出了当前最优反向差分进化算法(COODE)；Rahnamayan等[13]通过使用当前种群的中心点代替上述COODE中的当前最优点，提出了中心反向差分进化算法(CODE)；基于种群的迭代特性，Seif等[14]提出了基于迭代过程综合特性的综合反向差分进化算法(Comprehensive ODE)；为了进一步提高差分进化算法的局部搜索能力，Kushida等[15]和Wu等[16]分别提出了带指导矢量的AODE算法和带柯西校正算子的FODE算法。

为了解决当前多股簧动态模型参数识别过程中操作过程复杂、待识别参数多和求解精度低等问题，本文提出了多股簧参数识别的改进反向差分进化算法。该方法在没有最优解先验知识的情况下，通过使用适度占优个体的加权平均值作为反向计算的对称点，能够克服当前ODE及其改进算法中的隐含缺陷，有利于提高解的收敛速度；在变异计算过程中，使用正弦混沌映射产生缩放(变异)因子矩阵可以大幅度地提高种群的多样性。通过对某自动武器的复进簧进行动态加载试验并对含有量测噪声的试验数据进行测试，验证了本文方法的准确性和有效性；同时本文还发现，当前算法对试验数据中的噪声不敏感，即使添加7%的人工噪声仍能获得满意的结果。

1 改进的反向差分进化算法

1.1 标准DE算法

标准DE在种群初始化之后，经过变异、杂交和选择的多次循环操作，直到达到预定的迭代终止条件。在迭代过程中，种群大小NP、变异因子F和杂交概率Cr保持不变。四个操作过程简述如下。

(1) 初始化。设D为个体的维数，g为进化代数，则第i个体(目标向量)可以表示为：xi(g)=[xi,1(g),xi,2(g),…,xi,3(g)]，个体每一维上的取值可以表示为

xi,j(g)=Lj+randi,j(0,1)(Uj-Lj)

(1)

其中，1≤i≤NP，1≤g≤Gmax，Lj、Uj为第j维上的取值范围，randi,j(0,1)为介于0和1之间的一个随机数。

(2) 变异。以“DE/rand/1”变异策略为例来说明变异操作(更多的策略可以参考文献[4])，则变异向量为

vi(g)=xr1(g)+F(xr2(g)-xr3(g))

(2)

其中，r1、r2、r3为介于1和NP之间的互不相同的随机整数。变异后的个体有可能落在搜索边界之外，此时需采用随机方法重新生成。

(3) 杂交。以Binomial杂交为例，生成试验向量

(3)

其中，jrand为介于1和D之间的随机整数。

(4) 选择。基于一对一的竞争生存策略，从xi(g)和ui(g)中选择最优者保留到下一代。对于最小化优化问题min{f(x)}，选择机制可描述为

(4)

1.2 基于正弦迭代混沌系统的缩放因子

缩放因子对种群的多样性和算法的开发、探索能力至关重要。为了提高种群的多样性，多种随机化缩放因子策略被提出，比如，Salehinejad等[17]提出缩放因子的矢量随机化策略(Vectorized Random Mutation Factor)；Chelliah等[18]提出了基于Logistic映射的混沌随机缩放因子策略；Kumar等[19]基于Levy Flight的分布特性，提出使用随机Levy Flight行走步长作为缩放因子的方案也收到了较好的效果。

正弦混沌随机序列[20]是一个在[0,1]区间内波动的变量，它具有随机性、遍历性、非周期性以及对初值的极度敏感性，因此适合于产生(0,1)范围内的不重复伪随机数。将混沌随机序列应用于种群初始化和优化搜索时，可以避免算法陷入局部最优解。基于正弦迭代混沌系统的缩放因子为

(5)

其中，1

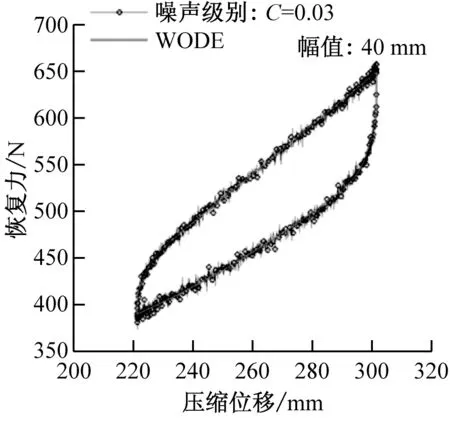
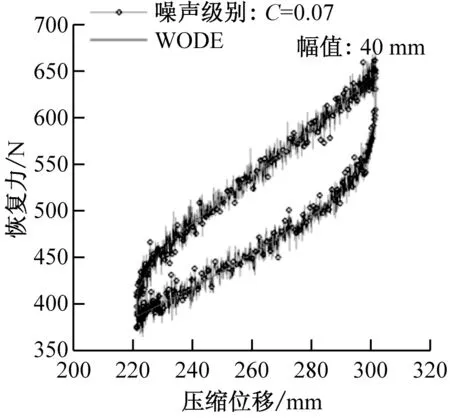
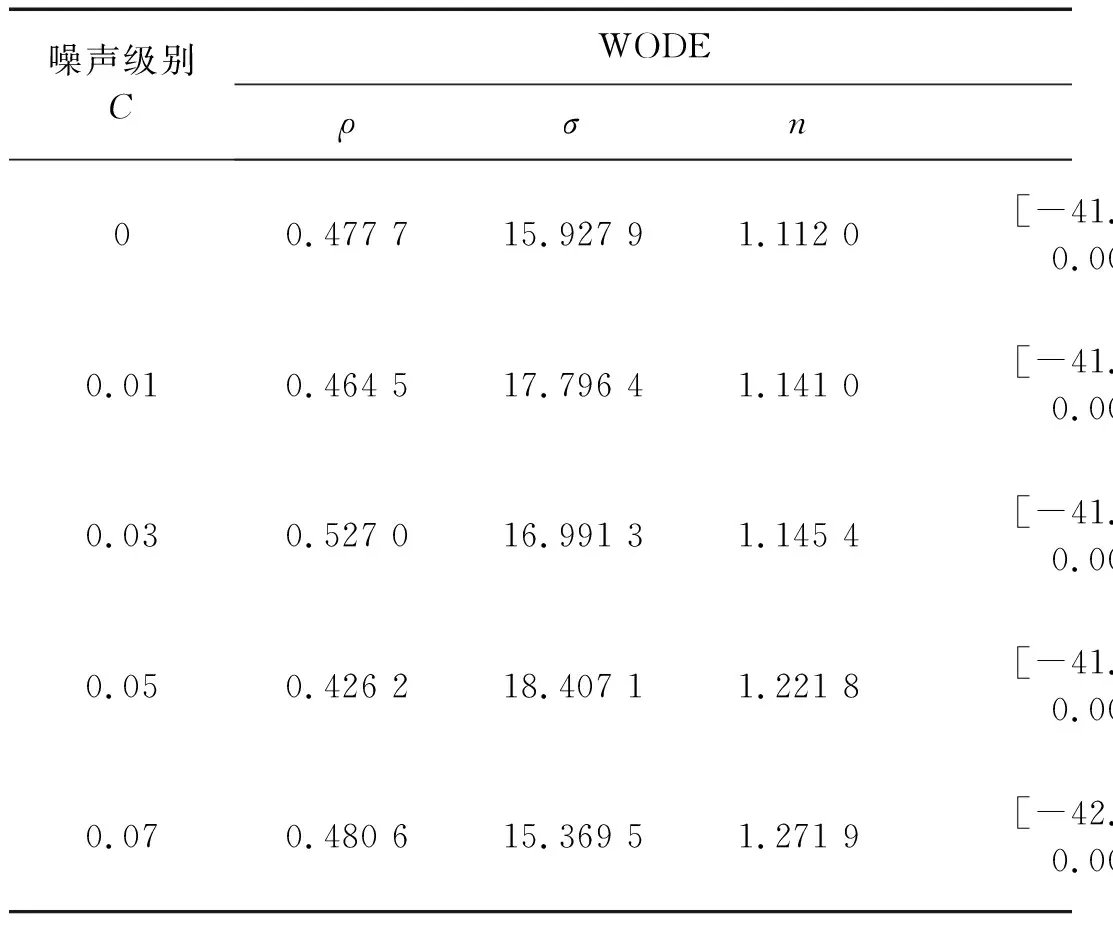
1.3 基于适度占优个体加权平均的反向差分进化算法(WODE)

定义1基于反向学习的优化(Opposition-based Optimization)：反向学习(Opposition-based Learning, OBL)的主要思路是同时评估当前解和反向解，并选择较好的解作为下一代的个体。假设实数x∈[a,b]，则其反向点可以被定义为

x*=a+b-x

(6)

将反向点概念推广到D维搜索空间，设当前解为x=[x1,x2,…,xD]，则其反向解x*=[x*1,x*2,…,x*D]可以被定义为：

x*j=aj+bj-xj

(7)

其中，xj∈[aj,bj]，j∈{1,2,…,D}。对于当前最小化优化问题，若反向解的适度值f(x*)≤f(x)，则x被x*取代，并称此过程为基于反向的优化。

定义2适度占优(Fitness Improvement)：在DE的选择操作中，若f(ui(g))≤f(xi(g))成立，则称个体适度占优[21]，且适度占优量Δf=f(xi(g))-f(ui(g))，适度占优量的大小表明个体经过变异和交叉后的进化程度。

定义3基于适度占优个体加权平均的反向学习策略(Opposition-based Learning using weighted average of fitness improvement individuals, WOBL)：设当前迭代过程中适度占优个体数量为N，则权重公式和反向学习的对称点(加权中心点)为

(8)

其中，i=1,2,…,N，N为适度占优个体的数量。

在迭代后期，适度占优个体的数量可能会小于3个，则此时的权重公式和反向学习的对称点可以用下式替代计算

(9)

总之，基于适度占优个体加权平均的反向点

x*j=2xw-xj

(10)

从式(6)和式(7)中可以看出，在标准ODE算法中，当前解和其反向解之间的对称点是求解区域边界的几何中心(如图2(a)所示)。对于大多数标准测试函数来说，函数全局最优解一般均位于函数定义域的几何中心，因此反向学习策略产生的反向解将会围绕这个几何中心，从而加快算法的搜索过程。

(a) 标准反向点

(b) 加权反向点

但面对现实世界的优化问题时，由于缺乏关于最优解的先验知识，全域最优解一般会偏离最初定义的几何中心(图2(b))，此时标准OBL产生的反向解将会远离全局最优解，导致算法进行多次无效的搜索，从而降低反向学习的效用和算法的收敛速度。而基于适度占优个体加权平均的反向学习策略(WOBL)，通过改变对称点的选择方式能够克服ODE算法中隐含的缺陷，并加快搜索全局最优解的进程。基于以上描述，下面给出改进ODE算法的流程,见表1。

1.4 基于适度占优个体加权平均的反向差分进化算法(WODE)的数值证明

本文所确定的WODE算法其收敛性可以通过数值实验来证明。下面通过建立三维球体寻优问题，分别假设球体中心点处于对称寻优空间和非对称寻优空间来验证WODE的成功率。三维空间球体寻优问题如下

(11)

对称寻优空间和非对称寻优空间分别为

(x,y,z)∈

(12)

可以看出在对称寻优空间中，球体的中心点位于寻优空间的中点上，而对于非对称寻优空间，球体的中心处于寻优空间的边缘；计算时设定种群维度为5D和6D，对比算法有标准ODE算法、GODE算法，每种情况独立计算10 000次。

计算结果如表2所示，可以看出在非对称区间的寻优过程中，由于缺乏关于寻优空间的先验信息，当全局最优解偏离寻优区间较远时，WODE比其他两种算法更具有优势，而在其他情况下这种优势就不太能够

表1 WODE算法的基本流程

表2 ODE、GODE和WODE的成功率

凸显出来。这一情况也同样适用于多股簧的参数辨识问题，因为研究人员事先并不清楚多股簧非线性刚度系数、放大因子、迟滞三参数的寻优区间，而使用WODE算法可以提高求解过程的稳健性，更能迅速地找到最优解。

2 多股簧非线性响应模型及其参数辨识

2.1 标准化Bouc-Wen迟滞模型

Ikhouane等[22]认为经典Bouc-Wen模型存在冗余参数，并提出精简参数的标准化Bouc-Wen迟滞模型，其数学表达式为

(13)

式中：F(t)为弹簧的恢复力；x、t分别为位移和时间；κx、κω分别为屈服后刚度系数和迟滞部分初始刚度；ω(t)为纯迟滞分量，对于任意的x和t，都有|ω(t)|≤1；ρ、σ、n为控制纯迟滞分量ω曲线形状的迟滞三参数。Ikhouane进一步指出标准化Bouc-Wen模型只有在满足σ≥0.5时才有物理意义，而且在实际应用中，若n<1则会使微分方程的右端出现无限大的量，从而导致计算发散。

2.2 修正的标准化Bouc-Wen迟滞模型

为了获得迟滞模型的非对称曲线，Zhao等提出使用非线性刚度系数和非线性放大因子来代替标准化模型中的线性屈服后刚度系数和迟滞部分初始刚度，两者均用多项式表示

(14)

式中：FE和FA分别是恢复力的非线性弹性部分和非线性放大部分；kEi和kAi分别是非线性刚度系数和非线性放大因子，N是多项式的阶数，一般取2阶或3阶。

从而得到可以描述多股簧动态响应的修正标准化Bouc-Wen迟滞模型

(15)

2.3 目标函数及计算参数初始化

当前算法采用三阶刚度系数，则多股簧系统待求解参数向量p为

p=[kE0,kE1,kE2,kE3,kA0,kA1,kA2,kA3,ρ,σ,n]T

(16)

(17)

(18)

因为部分模型参数有界限约束(σ≥0.5、n≥1)，所以设置初始参数的上、下界为

(19)

设置种群大小为NP=5D，交叉率Cr=0.5，最大允许迭代次数Gmax=500，迭代终止条件为成本函数的最大最小值之差小于1.0×10-6。改进算法的计算框架采用Rahnamayan等中所介绍的抗噪声ODE框架，反向操作的跳转率Jr=0.3。

3 多股簧力学实验、计算结果对比及其分析

3.1 多股簧力学实验

算法需要实测位移、恢复力数据作为输入参数，当前动力学试验装置为瑞士w+b公司生产的动态疲劳试验机，试验装置如图3所示。两根性质相同的多股簧被安装在上、下夹持件之间，并穿过各自的导杆以防止在加载过程中弯曲；下夹持件在试验过程中保持固定，上夹持件通过试验机夹头施加简谐激励信号x(t)=Asin(ωt)。多股簧的变形量为上夹头的位移，恢复力通过下夹头下的传感器测得。图4即为不同加载幅值下，加载频率为0.5 Hz时测得的复进簧力/位移数据。

图3 多股簧动力学试验装置

图4 实测的多股簧响应

3.2 参数辨识结果对比和分析

设置位移(幅值40 mm)、恢复力输入为多股簧动态试验的实测数据，设置速度输入为位移向前差分计算的结果，然后即可采用当前改进的ODE算法来识别多股簧模型参数。为了对比当前算法的性能，本文选择标准DE算法、ODE算法及其8种改进算法、三步法、VRF-DE算法作为对等比较算法，基本计算参数和当前算法保持一致，其他计算参数可以参考对应的参考文献。每种算法均独立运行50次，最大允许迭代次数Gmax=500。

为了评估算法的性能，本文使用参数识别结果仿真出来的恢复力和试验结果来计算恢复力的均方根误差(Root Mean Square Error，RMSE)

(20)

算法的成功率SR是另一个重要的评价指标，是指算法成功求解该函数优化问题的次数与总运行次数的比值。

几种算法的RMSE、迭代次数、运行耗时(以上均取成功收敛结果的平均值)、成功率如表3所示；可以看出在固定迭代次数下，本文的改进算法不仅用时最短而且成功率最高；其次是带指导矢量的AODE算法，这说明解的历史收敛方向可以用来指引候选解向全局最优解过渡；带Cauchy校正算子的FODE算法、GODE算法和标准ODE算法性能相当，它们在成功率和迭代次数上均优于标准DE算法，这说明反向学习策略对提高算法的收敛速度是有利的。

其他5种反向学习算法均表现不佳，这说明它们的反向学习策略对于当前求解问题的效用较小。文献[3]所介绍的三步法虽然成功率最高，但在求解前需要采用解析算法求出未知参数初值，不仅效率较低，而且参数的精度也较低。使用矢量随机缩放因子的VRF-DE在求解当前问题上表现较差，在规定的迭代次数范围内，其计算成功率为0，出现这种情况的原因可能在于该算法定义了不适当的缩放因子产生区间(F∈rand(0.5,1.5))。

表3DE(及其变种)、ODE(及其变种)和三步法的对比

Tab.3ComparisonofDE(anditsvariant),ODE(anditsvariants)andthree-stageidentificationmethod

算法RMSE/N迭代次数耗时/sSR本文算法1.771 3124.89123.2792%DE1.771 2286.73202.8066%ODE1.771 2203.11216.9174%GODE1.771 2229.14206.4570%QODE1.771 2242.18150.6264%QRODE1.771 4243.75145.3224%COODE1.771 4249.80196.5638%CODE1.773 1302.64144.9424%复合ODE算法1.771 2249.31165.0754%AODE1.771 2219.25239.6888%FODE1.771 7269.90243.8776%三步法2.745 5-130.56100%VRF-DE3.150 9500.0-0%

图5 ODE及其变种的性能对比

图6为多股簧非线性模型11个参数的估计结果，从图中可以看出，迟滞三参数中的σ和n收敛速度较慢，而非线性刚度和非线性放大因子等参数大约只需要四十次迭代即趋于收敛，这说明和其他参数相比，σ和n更容易陷入局部最优。当前改进ODE算法能够获得较好效果的原因是：在种群进化过程中，全局最优解xbest≠(Lj+Uj)/2，此时的反向学习会使反向个体偏离全局最优解。相反，使用本文的加权方案时，最优解xbest≈xw，由此产生的反向个体一般会分布在全局最优解附近，从而提高反向学习的效率，加强算法的全局搜索能力。与此同时，通过利用正弦混沌序列产生的缩放因子有利于提高种群的多样性，增强算法的局部搜索能力，因此算法在收敛性、稳定性方面优于其他对比算法。

(a) 迟滞部分参数估计曲线

(b) 非线性刚度系数估计曲线

(c) 非线性放大因子估计曲线

当然和其他几种成功率比较低的算法相比，当前算法的平均RMSE高出了0.000 1 N，出现这种情况的原因是：在迭代后期个体之间的差异比较小，而使用当前种群的加权平均值作为反向计算的对称点，这在一定程度上“模糊化”了对称点的最优特性，并导致“进化”后期反向学习的效能下降，使“进化”过程提前达到迭代终止条件而退出。因此，本研究的下一步着眼点是迭代过程中反向学习策略的自适应机制。

3.3 测量噪声对参数识别精度的影响

为了分析噪声对参数辨识过程的影响，本文对实测恢复力数据添加不同强度级别的噪声，噪声等级C分别为取为0.01、0.03、0.05、0.07，带噪声数据的生成表达式为

Fc=F0+CArRn

(21)

式中:Rn为标准正态分布的随机数向量；Ar为试验数据F0的幅值，由下式给出

(22)

将含有噪声的数据代入WODE，辨识结果图7所示。从图7(c)、(d)中可以看出，即使在量测噪声较高的情况下，本文算法辨识的结果依然能够较为精确地匹配试验数据；但是随着噪声等级的增加，辨识出来的力/位移曲线的光滑性变差，特别是在位移换向之后的加载过程中。本文算法识别的参数如表4所示，可以看出迟滞部分参数中的σ和n随着噪声等级的增加有增大的趋势，但这两个参数的增长率都在15%左右(C=0.05)，而非迟滞部分参数基本不变(为了表述的简洁性，表4已将kEi和kAi按照x的升幂写成向量形式kE和kA)，这说明当前改进ODE方法对试验噪声的不敏感性。

(a) C=0.01

(b) C=0.03

(c) C=0.05

(d) C=0.07

噪声级别CWODEρσnkEkA00.477 715.927 91.112 0[-41.584 5,2.162 9,0.004 0,0.000 1][43.411 0,0.343 3,-0.006 2,-3.362 8×10-5]0.010.464 517.796 41.141 0[-41.642 6,2.163 3,0.004 0,0.000 1][43.402 0,0.337 6,-0.006 1,-2.941 2×10-5]0.030.527 016.991 31.145 4[-41.779 6,2.135 8,0.004 4,0.000 2][43.569 2,0.343 8,-0.006 8,-3.742 0×10-5]0.050.426 218.407 11.221 8[-41.260 4,2.175 7,0.003 7,0.000 1][43.403 0,0.330 3,-0.005 8,-2.395 4×10-5]0.070.480 615.369 51.271 9[-42.183 2,2.166 8,0.004 2,0.000 1][43.556 6,0.388 3,-0.005 9,-7.066 6×10-5]

4 结 论

基于反向学习策略的ODE通过同时评价当前解及其反向解可以加快算法的收敛速度。在此基础上，本文通过引入基于适度占优个体加权平均的反向学习策略，并与基于混沌序列的缩放因子相结合，提出了改进ODE算法。该算法通过改变反向学习策略中对称点的选择方式，可以有效克服标准ODE算法在种群进化前期，反向点偏离全局最优解的弊端。通过使用该算法优化多股簧动态响应模型的目标函数，发现该算法能在较少的迭代次数内得到全局最优解。更进一步的实验结果表明，新算法对测量数据中的噪声不敏感，即使添加7%的人工噪声仍能获得满意的结果。