基于核密度估计的结构地震需求信息熵重要性分析

王秀振， 钱永久， 瞿 浩

(西南交通大学 土木工程学院，成都 610031)

对全面研究输出反应量受输入随机变量的不确定性影响，一般用灵敏性表示。众多学者对灵敏性进行了研究，Ratto等[1]将SDP(State Dependent Parameter)模型应用到基于方差的灵敏性测度分析中，提高了分析效率，这对复杂的结构系统模型进行灵敏性测度分析来说，可以大大降低抽样的样本数量；钟祖良等[2]对隧道的围岩压力相关的计算参数进行了敏感度分析，分析了各个计算参数对隧道围岩压力的具体影响规律；李思等[3]对比热容、围岩导热系数和赋存温度3个因素进行了对寒区隧道温度场影响的敏感性分析，发现3个因素的影响有明显的差异；叶继红等[4]在考虑了局部损伤对整体结构的影响的基础上，对结构冗余特性进行了响应敏感性研究，提出了以整体结构应变能对构件材料的敏感性极值这一冗余度评价的指标，对结构应变能敏感性的冗余度进行了评价。

全局灵敏性分析和局部灵敏性分析是灵敏性分析的两种类型，其中全局灵敏性分析，又称为重要性分析，可以从输入随机变量可能取值的范围，来全面衡量输入随机变量对输出反应量的影响情况[5]，这相对于局部灵敏性分析只能考虑输入随机变量取某些值时对输出反应量的影响，具有优势[6]。

重要性分析的方法有方差重要性分析、信息熵重要性分析[7]和矩独立重要性分析[8]等，本文采用核密度估计作为信息熵重要性分析的求解方法，以型钢混凝土框架结构为例，对影响结构地震需求的输入随机变量抽样后，进行信息熵重要性分析，并用方差重要性分析方法进行了对比，以验证其有效性。

1 信息熵重要性分析方法

1.1 信息熵的概念

变量的不确定性可以通过熵来度量，变量的不确定性越大则熵越大[9]。设离散型输入随机变量X的概率空间为

(1)

我们把X的所有取值的自信息的期望称为X的平均自信息量，通常称为信息熵(Information Entropy，IE)，简称熵(Entropy)，记为H(X)，即

(2)

对于连续性的输入随机变量X，假设X的概率密度函数为fx(x)，熵可以定义为

(3)

式中:E(·)表示数学期望；样本xk依据X的概率密度函数生成；DX表示输入随机变量的变化范围。

假设一个结构受多个输入随机变量的影响，输出反应量为

Y=g(X)

(4)

式中，X=(X1,X2,…,Xn)为输入随机变量。

根据信息熵理论，Y的熵可以定义为

(5)

式中:fY(y)是Y的概率密度函数；DY是Y的变化范围。

1.2 信息熵重要性分析指标的定义

对于式(4)的输出反应量Y=g(X)，如果输入随机变量X的值取为其实现值xi，这时Y的概率密度函数表示为fY|Xi=xi(y)。由于这时Xi已经消除了不确定性，所以输入随机变量Xi对输出反应量Y的信息熵效应定义是[10]

εi=|HY-HY|Xi=xi|

(6)

式中:HY是式(5)中输出反应量Y的原始熵，HY|Xi=xi是输出反应量Y的条件熵，定义如下

(7)

式(6)中定义的εi是输入随机变量Xi取其实现值xi时对输出反应量Y的效应。Xi对输出反应量Y的平均效应为

(8)

式中:E(·)表示数学期望，DXi表示输入随机变量Xi的变化范围，xij(j=1,2,…,N0)表示样本，依据Xi的密度函数生成，HY|Xi=xij表示Xi取xij(j=1,2,…,N0)条件下的条件熵。

1.3 信息熵重要性分析指标的性质

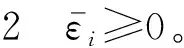
1.4 信息熵重要性分析指标的求解方法

对于给定数据y1,y2,…,yn，通过核密度估计，可以估计出该总体的概率密度函数[16]

(9)

式(9)是加权平均的形式，核函数(Kernal Function)K(·)是一个权函数，估计f(y)在点y的值时数据点的个数和利用的程度由核函数的值域和形状控制，核密度估计的优劣决定于核函数K(y)和带宽h的选取。常用的核函数如表1所示。

对于四次方核函数和Epanechikov核函数，不但只有离y的距离小于带宽h的点才起作用，而且起作用的数据的权重随着与y的距离减小而变大。

表1 常用核函数

1.5 计算流程

步骤1 首先采用低偏差的Sobol序列进行抽样，根据各个输入随机变量的联合分布密度抽取N个样本，用矩阵A表示为

(10)

步骤2 通过有限元软件OpenSees，将矩阵A中随机变量的样本值输入有限元模型，得到输出反应量Y的N个样本值yk(k=1,2,…,N)。

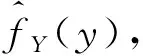
(11)

步骤5 类似于步骤2和3估计输出反应量Y的条件熵HY|Xi=xij。

2 工程实例1

某7层3跨的型钢混凝土框架结构，底层层高4 200 mm，标准层层高3 600 mm，如图1所示。楼板厚度120 mm，柱距6 000 mm，钢筋采用HRB335级钢，混凝土保护层厚度为25 mm，型钢强度等级为Q345，采用焊接H型钢，600×600柱中型钢为H400×400×11×18，500×500柱中型钢为H300×300×10×15，梁中型钢为H140×440×10×16，采用C40混凝土，梁柱截面配筋情况如表2所示，输入随机变量的详细信息见表3。

(a) 平面图

(b) 立面图

本例选取El Centro地震动记录(RSN6)，来自美国太平洋地震工程研究中心PEER中的强震数据库，双向作用(篇幅所限，仅列出结构横向的相关数据)。

图2给出了样本量为1 024时，4种地震需求与对应的结构质量样本值之间的散点图，可以看出，最大层间位移角需求和顶点位移需求大致与结构质量成正相关的关系，基底剪力需求和最大楼层加速度需求与阻尼比大致呈先正相关后反相关的关系，4种地震需求与其他各个输入随机变量的关系不再一一列出。

表2 输入随机变量的统计参数

表3 截面信息

(a) 顶点位移需求(b) 最大层间位移角需求(c) 基底剪力需求(d) 最大楼层加速度需求

图2 地震需求-结构质量关系

Fig.2 Seismic demand-structure quality relationship

本文得到了不同样本数条件下的各个输入随机变量对应的4种结构地震需求的重要性测度指标，如图3和图4所示，从图可知，在样本数为384以下时，各个输入随机变量对应的4种结构地震需求的重要性测度指标上下波动较大，样本数达到384时，各个输入随机变量对应的重要性测度指标的值基本不变，并且各个输入随机变量的重要性排序[20]不发生变化，可见本文的抽样方法需要的样本数量较少。

2.1 信息熵重要性测度指标

由图3可以看出，DA、Ms和fc对结构地震需求影响较大，其余输入随机变量的影响较小。

对于这4种结构地震需求而言，当样本数不小于384时，各个输入随机变量的信息熵重要性测度指标值变化较小，重要性排序基本不变。

(a) 顶点位移需求(b) 最大层间位移角需求(c) 基底剪力需求(d) 最大楼层加速度需求

图3 信息熵重要性测度指标

Fig.3 Information entropy importance measure index

2.2 方差重要性测度指标

输入随机变量的方差重要性测度指标如图4所示，由于篇幅所限，不再详细介绍方差重要性测度指标的求解过程，见参考文献[20]。

由图4可知，当样本数达到384时，各个输入随机变量的重要性排序基本不变，方差重要性测度指标值的变化也很小。

(a) 顶点位移需求(b) 最大层间位移角需求(c) 基底剪力需求(d) 最大楼层加速度需求

图4 方差重要性测度指标

Fig.4 Variance importance measure index

2.3 两种指标对比

信息熵重要性测度分析方法得到的各个输入随机变量的重要性测度指标，与方差重要性测度分析方法的结果列于图5。由图5可以看出，采用2种分析方法得到的输入随机变量的重要性排序基本一致，即使是有差别的，也是重要性测度指标的值非常小的情况下出现的；信息熵重要性测度指标与方差重要性测度指标2者的值不完全相同，这是由于两种方法分析指标的含义不同。

(a) 顶点位移需求(b) 最大层间位移角需求(c) 基底剪力需求(d) 最大楼层加速度需求

图5 重要性测度指标对比

Fig.5 Comparison of importance measure index

3 工程实例2

某型钢混凝土框架结构，与工程实例1中的结构类似，只是截面钢筋的配置以及地震动作用方式和选取的地震动记录不同，截面配筋如表4所示，选取的地震动记录如表5所示，PGA统一调整为0.6g，作用于结构纵向。

表4 截面信息

表5 地震动记录

基底剪力和最大层间位移角两种地震需求的重要性指标如图6所示。

(a) 基底剪力需求(IE)(b) 最大层间位移角需求(IE)(c) 基底剪力需求(VAR)(d) 最大层间位移角需求(VAR)

图6 重要性测度指标对比

Fig.6 Comparison of importance measure index

从图6可知，选取的7条地震动记录的重要性指标有一定的差异；对于多数地震动记录的基底剪力需求，fys的重要性测度指标最大，Es和Ec对应的重要性指标较小；对于多数地震动记录的最大层间位移角需求，DA、Ms和fys的重要性测度指标较大，Es和Ec对应的重要性指标最小。并且信息熵重要性测度指标和方差重要性测度指标的差别不大。

4 结果对比

工程实例1和工程实例2的加载方式不同、截面配筋不同、PGA也不同，作用于不同结构方向的2个工程实例中El Centro地震动记录的信息熵重要性测度指标如图7所示，由图7(a)可知，虽然具体的重要性测度指标值有差距，但DA、fc和fys对应的基底剪力需求重要性指标都较大，而Ec、Es和Ess对应的值都较小；由图7(b)可知，但DA、Ms和fys对应的最大层间位移角需求重要性指标都较大。

(a) 基底剪力需求(b) 最大层间位移角需求

图7 结果对比

Fig.7 Comparison of results

5 结 论

本文通过信息熵重要性分析方法，以型钢混凝土框架结构为例，研究了输入随机变量对4种结构地震需求的重要性，结论如下：

(1) 信息熵重要性分析方法得到的重要性排序与方差重要性测度分析方法得到的重要性排序基本一致，信息熵重要性分析方法是一种良好的重要性分析方法。

(2) 在用El Centro地震动记录和7条地震动记录分别对型钢混凝土框架结构进行重要性分析时，各个输入随机变量的重要性指标大小有普遍规律。

(3) 对于型钢混凝土框架结构，同一输入随机变量对4种不同的结构地震需求的影响水平有差别，但相对而言，Ms、DA和fc对4种地震需求的影响都较大，而Ec的影响都较小。

(4) 本文采用的抽样方法需要的样本数量较少，几百即可得到较好的结果。

通过与方差重要性分析方法对比可以发现，基于核密度估计的信息熵重要性分析方法是高效准确的方法。