多频涡激振动状态下柔性立管的时变水动力特性识别

刘 畅， 付世晓， 唐笑颖， 张萌萌， 任浩杰

(1.上海交通大学 海洋工程国家重点实验室，上海 200240;2.约翰·霍普金斯大学 机械工程系，巴尔的摩 21218;3.江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003)

在当前立管涡激振动(VIV)的预报中，涡激力载荷的构建直接决定着立管VIV预报结果的准确性。现有的用于预报VIV的半经验模型对涡激力载荷的构建均是基于刚性圆柱体单自由度(纯横流向或纯横流向)强迫振荡试验建立的涡激力系数数据库进行的[1-2]，其包括激励系数数据库和附加质量系数数据库。

然而，真实情况下VIV在顺流向(IL方向)与横流向(CF方向)都存在，并且二者相互耦合，这种运动上的耦合使得两个方向上的VIV水动力也相互影响[3-4]。为了揭示立管VIV在IL方向上和CF方向相互耦合作用下涡激振动响应的特性，Jauvtis等[5]开展了低质量比两维自激振荡实验，发现其泄涡模式与单自由度自激振荡不同：尾涡中出现了2T泄涡模式，即一个周期内单边泄落三个涡，这正是升力中含有三阶成分的原因。为了获得可更加准确预报立管CF方向的VIV的数据库，Dahl[6]开展了刚性圆柱体的二维强迫振荡试验，试验中将刚性圆柱体按照一定的顺流向/横流向振荡幅值比、横流向的振动频率(顺流向的振动频率假定为横流向的2倍)以及横流向&顺流向位移相位角进行简谐振荡。该试验获得了可用于预测立管涡激力尤其是3阶高频涡激力的水动力系数库。然而，该系数库包含的数据相对比较稀疏，且基于此系数库预报的涡激振动结果的准确性还未得到有效验证。此外，如何利用此方法研究柔性立管VIV高频响应下的水动力特性也有待研究。

刚性圆柱体强迫振荡试验能够方便地建立用于涡激振动预报的水动力系数库，但对于柔性立管，CF方向与IL方向的耦合效应以及三维流场等作用，使得柔性立管在洋流作用下的涡激振动响应极其复杂[7-11]，使得作用于柔性立管的水动力载荷不同于由刚性圆柱体单向强迫振荡试验获得的结果[12-13]。特别地，Vandiver发现了在CF方向3倍基频和IL方向4倍基频的高阶响应，表明真实柔性立管发生涡激振动时存在引起高频涡激振动响应的高频涡激力。Wu等[14]利用梁有限元状态矢量空间方程和基于最优控制理论的逆分析法获得了立管CF方向上的锁定频率的涡激力及其系数。Song等[15]采用模态分析法与欧拉梁动态响应控制方程相结合的方法，利用细长柔性立管缩尺试验测量的应变信息，结合最小二乘法获得了基频状态下的水动力特性。对于单一频率下的涡激力载荷，其被分解为与速度同相位的激励力和与加速度同相位的附加质量力，并进一步归一化为激励系数和附加质量系数。单一频率下的涡激力系数可以准确重构出单一频率下的水动力载荷。

然而由于缺乏有效分析手段，上述研究中均没有分析考虑多频耦合下柔性立管发生涡激振动时的水动力特性。仅使用锁定频率下的水动力系数无法准确预报多频涡激振动。

本文提出了遗忘因子最小二乘法识别柔性立管发生多频涡激振动下的时变涡激力系数。该算法在最小二乘法基础上，引入遗忘因子，其给予更接近当前时刻的数据更大的权重。这一修正提高了该算法对时变参数的敏感度，使其能够识别系统的时变参数。使用该方法获得了柔性立管发生多频涡激振动时横流向的时变涡激力系数，并将考虑多频耦合的涡激力系数与单一频率的涡激力系数进行了对比研究。

1 时变涡激力系数识别

当柔性立管发生涡激振动时，将CF方向VIV的功率谱密度最大处的频率看做为基频(下文中基频均依此定义)，则CF方向的振动通常由若干个奇数倍基频下的振动组成，即ω,3ω,5ω…，IL方向的振动通常由若干个偶数倍基频下的振动组成，即2ω,4ω,6ω…。其中CF方向上3倍以上基频的振动以及IL方向上4倍基频以上的振动被称为高频响应[16],在考虑浮力块，螺旋列板时响应频率会更加复杂[17]。 本文考虑更一般的情况，将立管CF和IL方向在节点z处的位移响应表示如下

y(z,t)=∑yi(z,t,ωi)i=1,2,3…

x(z,t)=x0(z)+∑xi(z,t,ωi)i=1,2,3…

(1)

式中:yi(z,t,ωi)代表CF方向单一频率ωi的位移响应；xi(z,t,ωi)代表IL方向单一频率ωi的位移响应,x0(z)代表平均弯曲位移。

以下将建立多频涡激振动状态下柔性立管的时变涡激力系数模型，仅以CF方向的涡激力系数推导为例，IL方向的涡激力系数推导与之相同。

立管在节点z处的位移响应y(z,t)可写成多个单频响应的线性叠加

(2)

式中:ωi为立管横流向涡激振动响应中的第i个圆频率；y0(z,ωi)为频率ωi下的位移幅值；φi为频率ωi下的相位角。对涡激振动位移进行微分，可以得到涡激振动响应的速度和加速度

(3)

在此情况下，立管节点z处的横流向的涡激力载荷

fCF(z,t)可表示为

(4)

式中:f(z,t,ωi)为频率ωi下的涡激力载荷，f0(z,ωi)为对应频率ωi下的涡激力振幅。

将其展开得

(5)

(6)

(7)

(8)

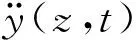
(9)

其中CLa(z,ωi)为节点z处频率ωi下的附加质量系数。

将式(6)和式(9)代入式(5)中有

(10)

其中：CLe(z,ωi)和CLa(z,ωi)即为表示CF方向节点z处在频率为ωi下的激励系数和附加质量系数。立管IL方向的水动力包括平均阻力和涡激力，涡激力系数推导与CF方向的涡激力系数推导类似。本文仅分析具有代表性的CF方向的涡激力载荷和涡激力系数。

从上式可以看出，当立管VIV出现多频响应时，需要多个频率下的激励系数和附加质量系数才能准确重构出水动力载荷。为了综合考虑多个频率的响应与载荷之间的耦合关系，本文求解多频耦合下时变的水动力系数，将式(10)改写为

(11)

其中

(12)

分别为多个单一频率下的速度，加速度，涡激力载荷叠加，以及多频叠加后速度时例的RMS值。

CLe(z,t),CLa(z,t)为时变的激励系数和附加质量系数，其代替式(10)中多个频率下的涡激力系数CLei(z,ωi),CLai(z,ωi),i=1,2,3…。时变的涡激力系数CLe(z,t),CLa(z,t)综合考虑了多个频率下的涡激力系数，以及各个频率之间的相互影响。

当以上求和符号中只含有单一频率的响应或载荷时，水动力系数的定义与定义的水动力系数一致。

随后引入遗忘因子最小二乘法(Forgetting Factor Least Square Method)(FF-LS)[18-19]识别式(11)的时变涡激力系数。该算法在最小二乘法的基础上，引入了遗忘因子，其给予更接近当前时刻的数据更大的权重。这一修正提高了该算法对时变参数的敏感度，使其能够准确识别系统的时变参数，从而获得时变涡激力系数。

将本文的涡激力载荷，涡激力响应表示成矩阵形式

fL=[fCF(z,t1),fCF(z,t2),fCF(z,t3),…,fCF(z,tL)]T

L=1,2,3,…

(13)

式中:t1代表初始时刻，tL代表当前观测时刻，对于本文的涡激力系数识别问题，z代表沿立管轴向位置，fL是节点z从t1时刻至tL时刻的涡激力载荷时例，HL是节点z从t1时刻至tL时刻的的涡激振动速度，加速度时例，θ(L)是立管在节点z，tL时刻的未无因次化的涡激力系数。以上三个矩阵的每一行代表某一时刻的采样数据。

式(11)中的时变涡激力系数识别可以表示为识别参数θ(L)L=1,2,3,…的时例，其满足

fL=HLθ(L)L=1,2,3,…

(14)

式中：t1,t2,t3,…,tL代表采样时间，并且共有L组数据被采样。式(14)表示所有tL时刻之前的数据被用于识别时变参数θ(L)。在下文中，在tL时刻的参数θ(L)简写为θ。

随后，将涡激力载荷时例和涡激振动速度，加速度时例乘上一个数据权重。观测数据距离当前时刻tL越近，该权重值越大。特别的，对于当前时刻tL的数据权重为β0=1, 对于初始时刻t1的数据权重为βL-1(β为常数，并且满足0<β≤1)。加权后的涡激力载荷表示为

(15)

同样的，加权后的涡激振动速度和加速度表示为

(16)

时变涡激力系数需要满足下式

(17)

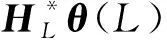
(18)

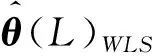
(19)

根据如下的向量微分公式

(20)

式 (19)成为

(21)

(22)

将式 (15)和(16)代入式(22)

(23)

式中:μ=β2，0<μ≤1，μ称为遗忘因子,ΛL是加权矩阵，其对角元素满足，Λ(L)=1，Λ(k-1)=μΛ(k),非对角元素为零。该算法本质上对不同时刻的数据进行加权，距离当前时刻越远的数据，其权重越小，如图1所示。

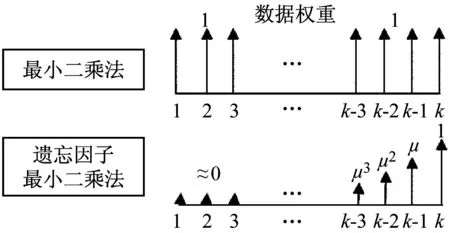
图1 遗忘因子最小二乘法数据权重示意图

Fig.1 Schematic of data weight for forgetting factor least squares method

2 识别方法验证

为了验证本文提出的遗忘因子最小二乘法能够准确识别时变的涡激力系数，本章使用质量-弹簧-阻尼器模型对该算法进行验证。构造如下问题。

(24)

式中：M,C,K分别为质量块的质量，阻尼器的阻尼，以及弹簧的刚度，均为常数。

(25)

min[Freal(t)-Frecon(t)]2

(26)

设定M=10，C=40，K=1 500，模拟20 s的运动，每0.01 s取一个观测数据

设定运动信号为

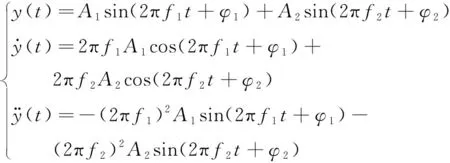
(27)

其中振动幅值A1=0.01,A2=0.005,振动频率f1=1 Hz，f2=3f1=3 Hz,相应的圆频率为ω1=2πf1,ω2=2πf2,初始相位角为φ1=φ2=0。

图 2是多频叠加下的质量块运动信号(位移，速度及加速度)的时例。

使用式(24)构造出该运动响应对应的载荷，对于多频运动响应情况下，原系数求解问题(28)不再具有理论解

(28)

使用最小二乘法求得CLe(t)=39.55,CLa(t)=4.187，但是通过这两个系数重构的力信号与真实力信号差距较大(图3)。这是因为在考虑多频耦合时，使用定常的激励系数和附加质量系数不足以准确重构出力信号。

使用遗忘因子最小二乘法可获得质量-弹簧-阻尼系统的时变激励系数与附加质量系数，通过该系数时例重构出的力信号与真实力信号之间吻合较好(图3)，此时的激励系数和附加质量系数随时间周期性变化(图4)，这是多频之间耦合作用引起的。结果表明本文所提出的遗忘因子最小二乘法能够有效的识别涡激振动响应下多频涡激力系数。

图2 ω1和ω2叠加下的运动信号时例(位移，速度，加速度)

Fig.2 Time history of motion superposition underω1andω2(displacement, velocity and acceleration)

3 多频涡激振动下柔性立管的时变水动力特性

3.1 模型试验

本文中均匀流场下细长柔性立管水动力模型试验在拖曳水池中进行，立管模型横置于水池中，立管两端利用万向节与端部装置进行连接。端部装置可以为立管模型提供恒定预张力。试验中通过拖车带动立管在拖曳水池中匀速运动的方法模拟均匀来流。试验装置如图5所示。

图3 真实涡激力，使用最小二乘法识别的系数重构的力信号与使用遗忘因子最小二乘法识别系数重构的力信号对比

Fig.3 Comparison among real force, force reconstructed from coefficients identified by LS method and that identified by FF-LS method

图4 质量-弹簧-阻尼器激励系数和附加质量系数时例

Fig.4 Time history of excitation coefficient and added-mass coefficient in mass-spring-dashpot system

图5 均匀流场下柔性立管水动力模型试验装置

试验采用的立管模型为缩尺模型，模型水动力外径为31 mm，有效长度为7.9 m，细长比为263。立管模型的结构参数如表1所示。

表中的结构阻尼比为立管模型在空气中的结构阻尼比，通过立管模型在空气中的自由衰减试验获得，在此不做详细介绍。

试验中使用光纤光栅应变传感器测量立管模型表面的应变响应信息。光纤光栅应变传感器分别布置于立管模型的CF1、CF2、IL1以及IL2四个方向，用于测量模型在此四个方向上的应变，即CF1、CF2、IL1和IL2，如图6所示。立管模型的表面分别布置有88个传感器，其中CF1，CF2方向上各19个传感器，IL1和IL2方向上各25个传感器。横流向与顺流向上的传感器均均匀分布。光纤光栅传感器的采样频率为250 Hz。这里需要指出的是，立管模型每个方向上所有测点的应变片均埋藏在一根直径为125～140 μm的光纤中。在模型制作时，此光纤粘贴在模型的表面，并在光纤的外面覆盖一层厚度为0.5 m的热缩管，以保证模型表面的光滑性。因此立管模型表面布置的应变片不会影响模型周围的流场以及模型的振动响应。此外，试验中，立管模型上四个方向上所有测点的应变信息同时采集，因此，不同测点处测得的应变信息之间没有相位延迟。

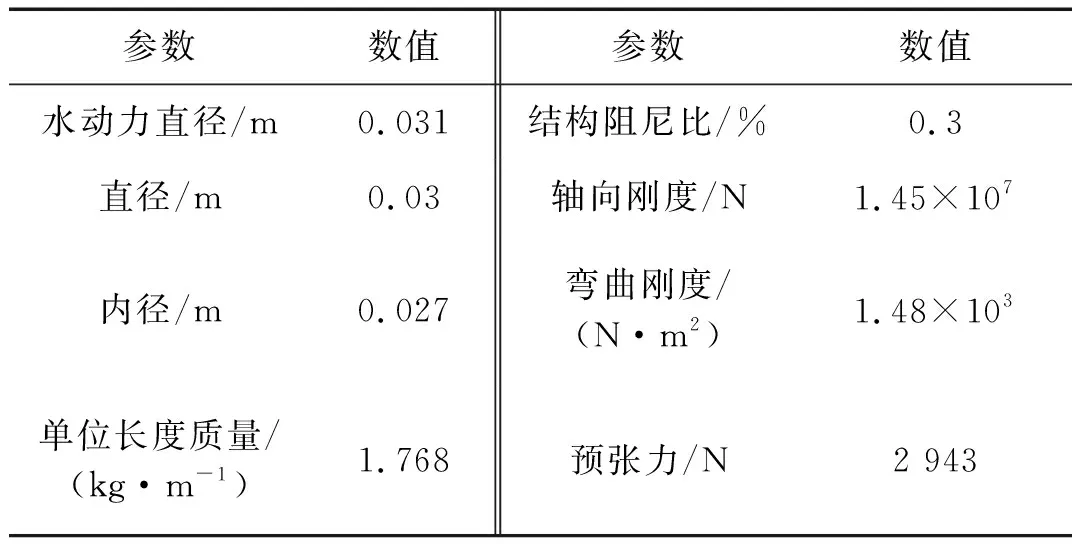
表1 立管模型参数

图6 光纤光栅应变传感器安装示意图

Fig.6 Arrangement of strain gauges on the surface of the riser model

本文选取具有代表性的的实验工况：均匀流2.8 m/s下CF方向的涡激振动响应进行分析，下文不再赘述。该工况对应雷诺数为6.4×104。

3.2 涡激振动响应与涡激力

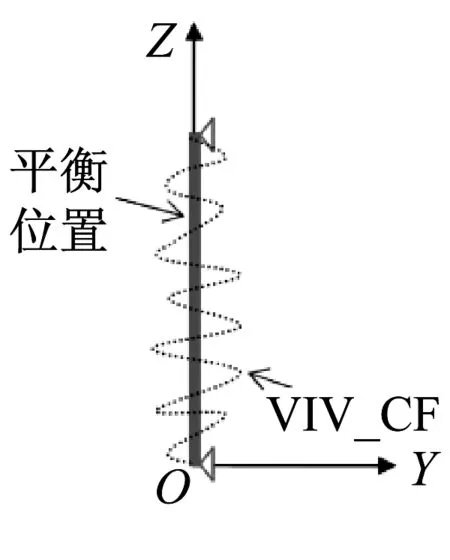
图7(a)表示的是流场中承受张力T0的柔性立管，立管的轴线沿坐标系的Z轴，流场方向与坐标系的X-Z面平行且垂直于立管的轴线。此时，立管的IL面为坐标系的X-Z面，立管的CF面为坐标系的Y-Z面。由于流体具有黏性，流场会在立管的IL面上会产生不随时间变化的阻力，即：平均阻力。在平均阻力的作用下，立管会发生弯曲变形，偏离其原始位置(Original position)，本文中将此弯曲变形称为平均弯曲，立管发生平均弯曲后的位置称为平衡位置(Equilibrium position)，如图7(b)所示。此外，当流体流经立管表面时会在立管的周围产生周期性的泻涡，周期性的泻涡会在立管的CF面内和IL面内产生均值为零的周期性的涡激力，使得立管在CF与IL面内相对于平衡位置发生振动，即：涡激振动(VIV)，如图7(b)和(c)所示。因此在流场作用下，柔性立管的水动力载荷包括：CF方向的涡激力，IL方向的平均阻力和涡激力，相应的，立管的总体结构响应包括：CF方向的VIV响应；IL方向的平均弯曲响应和VIV响应。

(a)

(b)

(c)

Fig.7 Response of a submerged flexible riser with a tensional force under uniform flow

根据有限元理论，立管的有限元动态响应控制方程如下式

Mδ″+Cδ′+Kδ=F

(29)

式中：M,C和K分别为立管的质量矩阵、阻尼矩阵以及刚度矩阵；δ为立管的位移矩阵，δ′和δ″分别为位移矩阵δ对时间的一阶导和二阶导，即：速度矩阵和加速度矩阵；F为立管的水动力载荷矩阵。对于节点个数为N，节点自由度为6的立管，矩阵M,C,K的维数为6N×6N；矩阵和F的维数为6N×1。

对于承受轴向张力的立管，其单元刚度矩阵Ke包括两部分

(30)

C=αM+βK

(31)

式中：a与b为Rayleigh阻尼系数，可由立管的固有频率及结构阻尼比求得。

立管的位移矩阵δ可表示如下

δ=[δ1,δ2,…,δN]T(i=1,2,…,N)

(32)

式中:N为立管的节点个数；δi为立管节点i处的位移矩阵

(33)

式中：zi为立管在轴向的拉伸位移；xi和yi为立管在IL和CF面内的线位移；θzi为立管绕其轴线，即z轴的扭转角；θyi和θxi为立管在IL面和CF面内发生弯曲时产生的绕y轴和x轴的角位移。在本文分析立管水动力载荷时忽略立管沿轴向的扭转变形，即假定：θx=0。

立管的轴向拉伸位移可由立管表面的拉伸应变求得；IL和CF方向的弯曲位移可以采用模态分析法[21]根据立管表面的弯曲应变求得。

立管的角位移θyi和θxi可采用中心差分法根据立管CF和IL面内的线位移x和y求取。

在根据立管的结构参数建立起立管的质量矩阵M、刚度矩阵K以及阻尼矩阵C后，如已知立管的结构响应矩阵δ,δ′,δ″，根据逆有限元方法，即可在获得流场作用下VIV发生时立管的水动力载荷F。由于求解水动力载荷的逆有限元方法与Song等使用的方法相同，且其准确性已经过验证，本文不再赘述，详细验证结果可参见其论文。

图8和图9分别为涡激振动应变的时空分布和涡激振动应变的功率谱密度沿立管轴向分布。可以看出，该工况下CF方向的涡激振动应变包含多个频率成分。定义涡激振动应变的功率谱密度最大的频率为基频，本文记为ω1=2π×f1=2π×16.8 rad/s，同时该应变响应中出现了三倍基频的高阶响应，本文记为ω2=2π×f2=2π×50.4 rad/s。

使用模态分析法重构出涡激振动位移并使用上述逆有限元理论根据VIV位移重构出柔性立管发生VIV时的总体水动力载荷，其在下文的分析中作为真实涡激力载荷。图10是CF方向的涡激力时空分布。图11是水动力载荷的功率谱密度沿立管轴向分布。从图中可以看出，柔性立管发生涡激振动时，在CF方向出现了三倍基频3ω下高频涡激力，Dahl在两自由度刚性圆柱体自激振动试验中也发现了CF方向的三倍基频涡激力，并认为是由于高雷诺数下，立管两自由度的运动引起了2T泄涡模式引起的。

从涡激力的功率谱密度分布图(图11)中可以看出，高频成分的作用不可忽略。

图8 涡激振动应变的时空分布

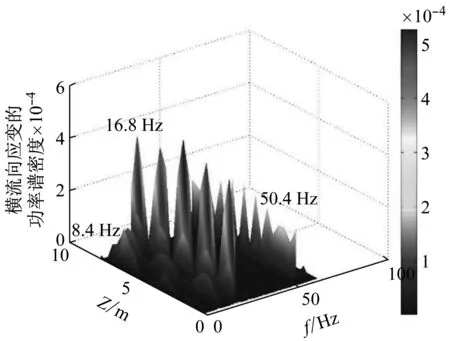
图9 涡激振动应变的功率谱密度沿立管轴向分布

图10 涡激振动水动力载荷的时空分布

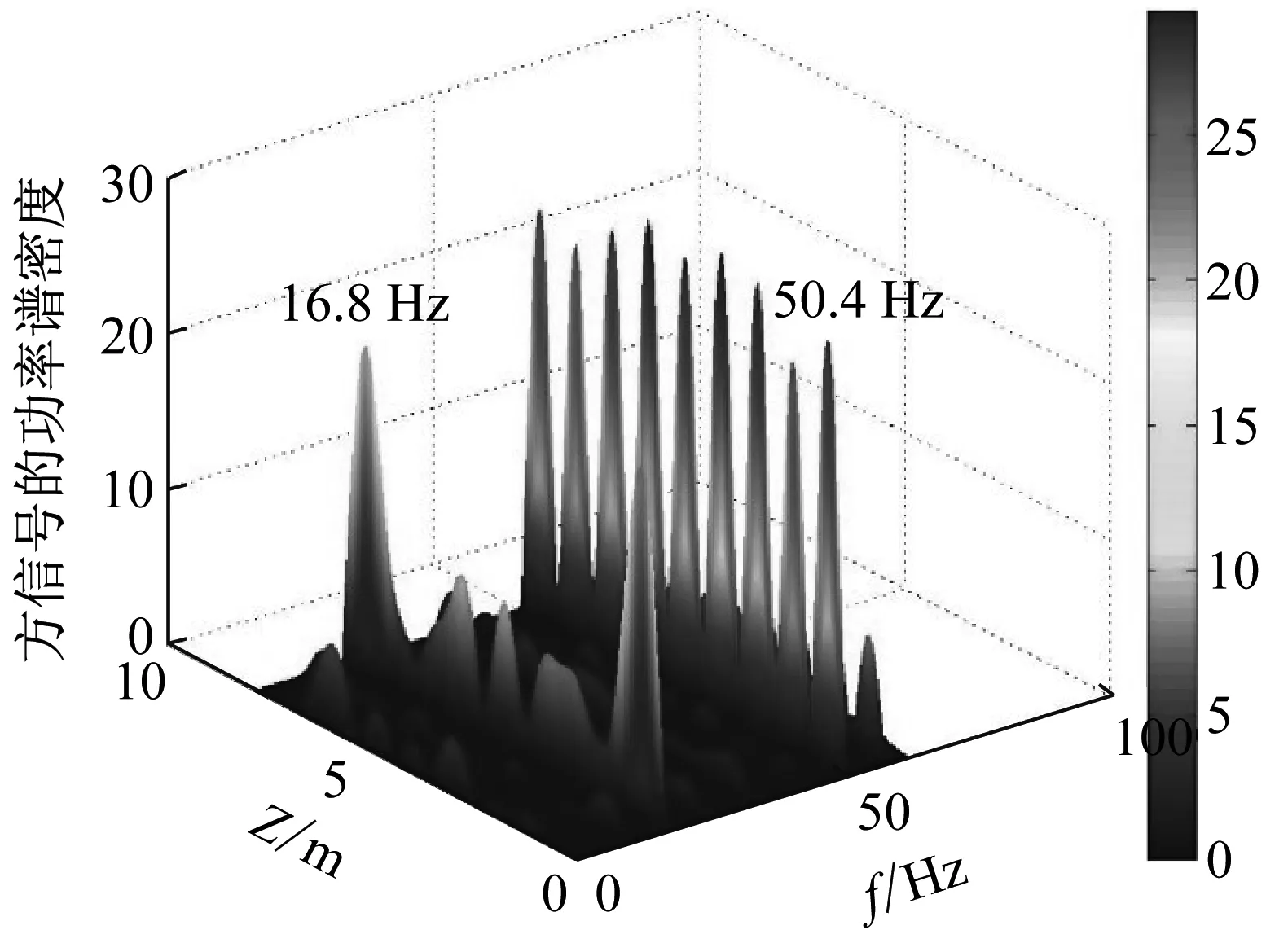
图11 涡激振动水动力载荷的功率谱密度沿立管轴向分布

3.3 时变涡激力系数

首先，使用带通滤波器将涡激力载荷，涡激振动速度，涡激振动加速度分解至基频ω1=2π×16.8 rad/s和高频ω2=2π×50.4 rad/s下，并分别记为

滤波带宽分别为16～17.5 Hz和50.1～50.7 Hz。将基频和高频下的涡激振动响应和涡激力载荷进行线性叠加

(34)

图12是基频ω1，高频ω2，基频与高频叠加的涡激力RMS值与滤波前涡激力RMS值轴向分布对比，发现仅考虑基频ω1或仅考虑高频ω2时，其RMS值较滤波前的涡激力载荷偏小，而同时考虑基频ω1，高频ω2下的涡激力载荷时，其与滤波前的真实涡激力较接近。

图12 立管涡激力载荷RMS值沿立管轴向分布

Fig.12 Axial distribution of RMS value of vortex-induced force (solid line: superposition of basic frequencyω1and high frequencyω2, dotted line: before filter)

将式(34)代入式(11)的时变涡激力系数模型中，则需要求解的时变涡激力系数CLe(z,t),CLa(z,t)需满足下式

(35)

随后使用本文提出的遗忘因子最小二乘法识别出上式中的待求解的时变涡激力系数。

图13和图14是多频耦合下的激励系数与附加质量系数时空分布，可以看出考虑多频耦合作用时，激励系数和附加质量系数会发生周期性变化，且包含多种频率成分。

图13 基频ω1与高频ω2耦合下的激励系数时空分布

Fig.13 Time-space distribution of excitation coefficient under coupling between basic frequencyω1and high frequencyω2

图15和图16是不同算例下涡激力系数沿立管轴向分布(实线：时变激励力系数的时间平均值；圆：基频ω1下的激励力系数；三角：高频ω2下的激励力系数)。

图14 基频ω1与高频ω2耦合下的附加质量系数时空分布

Fig.14 Time-space distribution of added-mass coefficient under coupling between basic frequencyω1and high frequencyω2

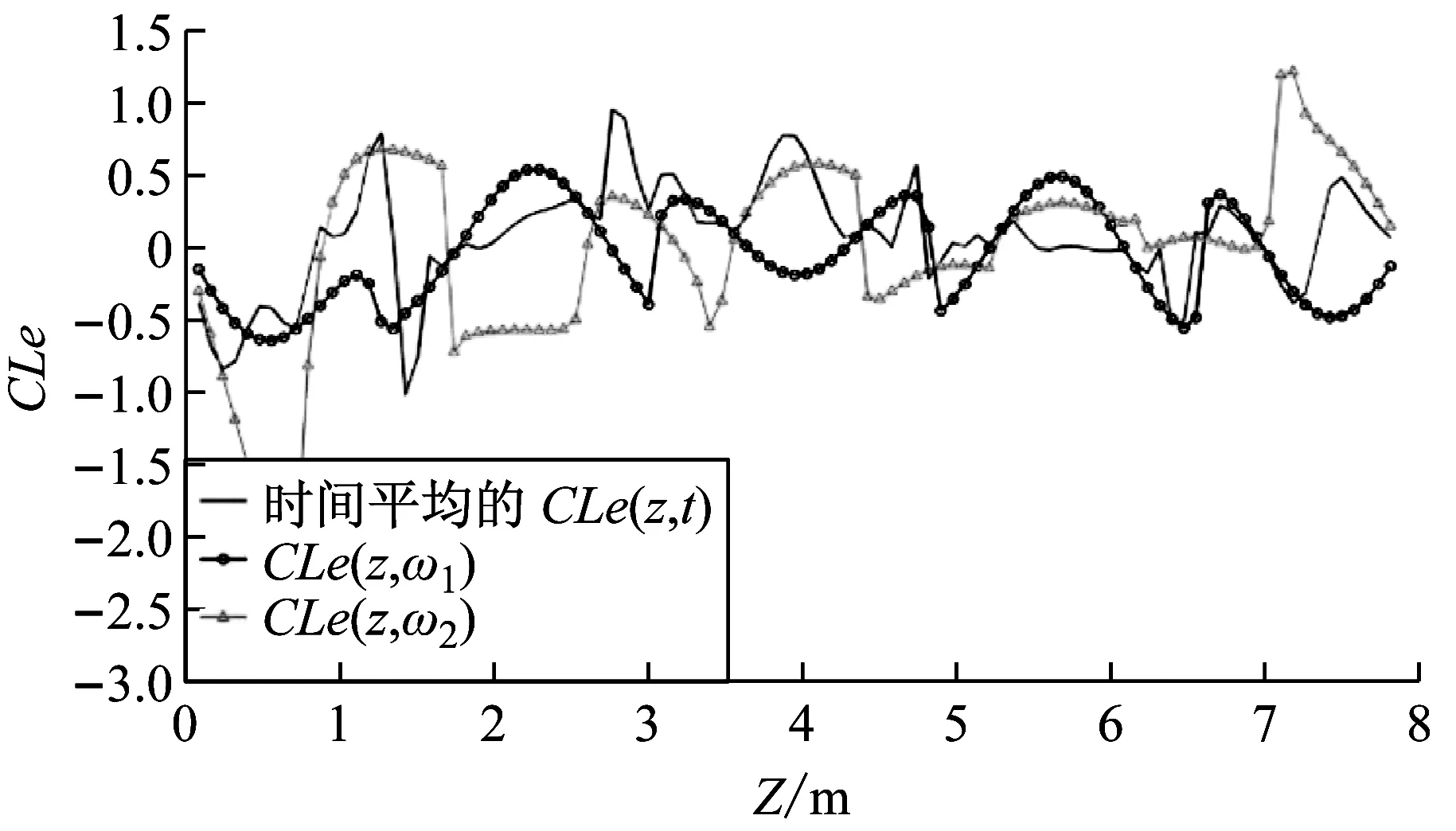
图15 激励系数沿立管轴向分布(实线：时变激励力系数的时间平均值；圆：基频ω1下的激励力系数；三角：高频ω2下的激励力系数)

Fig.15 Axial distribution of excitation coefficient (solid line: Time-average value of time-varying excitation coefficient under coupling between basic frequencyω1and high frequencyω2, round: excitation coefficient under basic frequencyω1, triangle: excitation coefficient under high frequencyω2)

图16 附加质量系数沿立管轴向分布(实线：时变附加质量系数的时间平均值；圆：基频ω1下的附加质量系数；三角：高频ω2下的附加质量系数)

Fig.16 Axial distribution of added-mass coefficient (solid line: Time-average value of time-varying added-mass coefficient under coupling between basic frequencyω1and high frequencyω2, round: added-mass coefficient under basic frequencyω1, triangle: added-mass coefficient under high frequencyω2)

通过对比可以得出以下结论：考虑多频耦合时的时变涡激力系数时间平均值沿立管的轴向分布与基频下的涡激力系数沿立管轴向分布有所区别，这是高频响应和高频涡激力耦合作用的结果。

为了验证识别的时变涡激力系数能够准确重构出涡激力载荷，使用获得的涡激力系数CLe(z,t),CLa(z,t)依据下式重构出涡激力载荷

(36)

图17是根据识别获得的时变涡激力系数重构出的涡激力载荷与真实涡激力在立管中点的时例曲线对比，两者基本一致，表明该识别方法获得的涡激力系数重构得到的涡激力载荷可以准确还原真实涡激力载荷的分布特性。

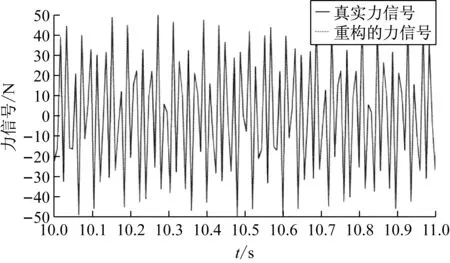
图17 使用FF-LS识别得到的多频耦合下的时变涡激力系数重构的水动力载荷与真实水动力载荷对比

Fig.17 Comparison between real vortex-induced force and force reconstructed from time-varying vortex-induced force coefficients identified by forgetting factor least square method

4 结 论

本文提出了遗忘因子最小二乘法识别考虑多频耦合的时变涡激力系数。首先使用质量-弹簧-阻尼的理想模型验证了遗忘因子最小二乘法可以识别系统的时变参数。其可以考虑多频之间的耦合效应，且识别的时变参数可以准确重构出力信号。随后应用该方法识别了基频与高频耦合作用下，柔性立管发生涡激振动下横流向的时变涡激力系数。结果显示柔性立管发生多频涡激振动时，其涡激力系数会周期性变化，且涡激力系数的时间平均值亦不同于基频下的涡激力系数，这是基频与高频耦合作用的结果。使用识别的时变涡激力系数进行反演重构得到的涡激力与真实涡激力相吻合，验证了该方法识别多频耦合下的时变涡激力系数可以准确重构涡激力载荷。本文后续工作请参见文献[22]。