并联式六维加速度传感器的解耦参数辨识及其扰动分析

尤晶晶， 符周舟， 李成刚， 吴洪涛， 王 进

(1.南京林业大学 机械电子工程学院，南京 210037；2.江苏省精密与微细制造技术重点实验室，南京 210016；3.南京林业大学 汽车与交通工程学院，南京 210037；4.南京航空航天大学 机电学院，南京 210016)

微细切削加工机床是实现精密微细切削技术的关键设备，工作过程中产生的切削振动将使工件与刀具之间的相对位姿发生微幅变动，这使得微小尺寸零件的表面粗糙度等性能质量会受到较大影响[1-2]。三维位形空间内物体的运动维数为6，包括沿(绕)三个正交坐标轴方向的平移和旋转，与此对应的三维线加速度矢量和三维角加速度矢量合称为“六维加速度”。因此，通过实时测量刀具的六维加速度信息并反馈给机床的驱动控制系统，理论上可以实现工件与刀具相对位姿的调整以提高加工质量。除此之外，机器人、航空航天、生物医疗等高、精、尖领域均离不开六维加速度信息的测量。传统的测量设备为3个正交加速度计和3个正交陀螺仪的组合体[3]，它们分别检测载体系下的三维线加速度、角速度，进一步运用角速度与角加速度、姿态矩阵之间的微积分关系，解算出惯性系下的六维加速度。

由于机械陀螺不能承受较高的线加速度冲击，而光纤陀螺和激光陀螺不但制造、使用成本高，而且受温度、磁场等外界因素的影响较严重[4]，越来越多的学者开始考虑用加速度计代替陀螺仪测量载体的角运动。Wang等[5]提出了一种基于共面的6加速度计组合方式的六维加速度传感器，具有结构紧凑、安装方便的优点；Zou等[6]提出了一种基于8个二轴加速度计的圆柱体构型方案，具有尺寸小、可靠性高、集成度高的优点。然而，研究表明[7-8]，多个加速度计安装位置、方向的微小偏差会对载体角速度的计算精度产生较大影响，因此，全加速度计配置方案的工程实现较为困难。鉴于此，Sun等[9]提出一种“低成本、无陀螺、单质量块”的设计方案，即所有加速度计共用一个惯性质量块；所构建的一体化六维加速度传感器模型具有尺寸效应误差小、灵敏度高的优点，但存在量程小、工作频带窄和各向同性差等缺陷。

考虑到台体型并联机构具有承载能力强、动态特性好、各向同性度高等固有特性[10]，尤晶晶等[11-12]提出了一种基于台体型并联机构的一体化六维加速度传感器模型，所构建的完全解耦算法具有不依赖于载体运动规律、实时性好和计算精度高的优点。解耦算法的前提是已知了系统的解耦参数(后文也称之为“参数项”)，然而，由于加工、装配过程中不可避免地存在操作误差，而且敏感元件容易受到环境因素的影响，因此，每一台传感器样机在不同工作环境下的参数项都不一致，需要预先辨识。

并联式六维加速度传感器属于强非线性耦合系统，其参数项的个数多且辨识困难。尤晶晶[13]通过设定待测运动的线阈频和角阈频，将解耦方程近似变换成四组含部分特征量的子方程，进而提出一种“四步法”的参数辨识算法。然而，由于两个阈频均需要通过多次实验试凑获得，且后三组参数对阈频值的敏感程度高，故该算法实现起来较繁琐，不便于推广应用。在此基础上，本文通过输入项的坐标反变换，从解耦方程中分离出三组参数项，进而通过构造三种独立运动模式下的辨识方程，提出一种新的参数辨识算法；进一步地，分析了输入、输出数据的扰动对辨识精度的影响，发现可以通过最少次数的实验最真实地还原参数项；最后，通过仿真和试验对辨识算法及其扰动模型的准确性、有效性进行了验证，同时对新、旧算法的精度和效率进行了对比。

1 结构模型及解耦方程

并联式六维加速度传感器的结构模型及结构示意图分别如图1、2所示，包含12条相同支链，它们均由1个圆柱体压电陶瓷和位于其两端的2个弹性球铰链串联而成。每两条支链为一组，相互垂直布置且共用一个球铰链，6个共用球铰链分别固结在正方体质量块的上后棱、上左棱、右后棱、下前棱、下右棱和左前棱的中点。十二条支链的另一端与嵌套在外壳内的副板固结，通过调节6块副板中央的预紧柱并配合外壳上的锁紧板，可以同时对所有支链预紧、防松。

1-质量块；2-外壳；3-压电陶瓷；4-弹性球铰链；5-副板；6-预紧柱；7-锁紧板

图2 并联式六维加速度传感器的结构示意图

当传感器外壳上作用待测的六维加速度时，位于外壳内部的质量块会受到相反方向的广义惯性力，进而压缩(拉伸)12条支链。尤晶晶等的研究表明，当独立支链的数目不小于6时，通过测量所有支链的轴向力，理论上能够反推出外壳的六维加速度信息。

分别在参考地面、传感器外壳上固连坐标系{1}和{2}，初始状态下它们重合，且坐标原点位于质量块的质心处，坐标轴方向见图2。在忽略支链微小变形的影响下，并联式六维加速度传感器的解耦方程在坐标系{1}内可以表示成两组解析式

(1)

(2)

2 解耦参数的辨识模型

2.1 解耦参数的确定及敏感度分析

六维加速度传感器在实际工作时，支链轴向力的测量是通过压电陶瓷两极化面的输出电压转化而来，两者之间近似满足线性关系

(3)

其中

将式(3)代入式(1)、(2)，并将六维加速度反向投影至坐标系{2}内(坐标反变换)，这样，具有强非线性耦合特性的两组解耦方程就被等效替换成6个形式简单、结构对称的纯线性解耦方程

(4)

(5)

(6)

(7)

(8)

(9)

其中

J=

(J1,J2,J3,J4,J5,J6,J7,J8,J9,J10,J11,J12,J13)

(10)

其中

将式(4)～(9)代入式(10)

(11)

基于拓扑构型内的固有几何约束关系，冗余构型传感器的输出量之间还满足如下6个协调方程

(12)

(13)

(14)

(15)

(16)

(17)

联列求解方程组(4)～(9)、(12)～(17)，得到12个输出项的解析表达式

(18)

其中

表1 输入项对参数项的事前敏感度

结果显示：

(1) 输入项对前12个参数项的敏感度等级相同；在其它条件均已确定的前提下，支链的刻度因子越大或者质量块的质量越小，则这12个参数的偏差对输入项的误差影响越小。

(2) 第13个参数不影响输入项中的前3个量，只影响后3个；在其它条件均已确定的前提下，质量块的边长越大，则该参数的偏差对输入项的误差影响越小。

2.2 解耦参数的辨识算法

六维加速度传感器的参数辨识是指在已知输入运动和输出电压的前提下，反推出全部的参数项。其中，输入运动量是通过将待辨识传感器与标准加速度传感器“背靠背”地安装在同一个试验平台上感应相同的运动，并读取后者的输出数据获得；输出电压量是通过读取前者的输出数据获得。

当试验平台输出纯线运动时，姿态矩阵为单位矩阵，角加速度为零矢量，后三个输入项均为零。此时，式(18)可以表示成矩阵形式

AX=U

(19)

其中：

A=diag(A1,A3,A1,A2,A3,A2,A1,A3,A1,A2,A3,A2)

理论上，通过调整支链预紧力，可以避免压电陶瓷受拉而导致的输出信号失真的问题[14]。然而，考虑到预紧力可能存在偏差，下面将辨识方程(19)再拆解成两个结构相同的子方程

A+X+=U+

(20)

A-X-=U-

(21)

其中

A+=diag([A1]1,[A1]1,[A2]1,[A3]1,[A2]1,[A3]1)

A-=diag([A3]2,[A2]2,[A3]2,[A1]2,[A1]2,[A2]2)

式中：[·]1、[·]2分别对应第1、2组辨识实验数据。

在选取辨识实验的输入数据时，式(20)中的A1、A2、A3均大于零，式(21)中的A1、A2、A3均小于零，这样就能够确保辨识方程中的输出数据均有效且可信。

计算两个子辨识方程的系数矩阵的行列式

(22)

这表明，两个子参数项均存在确定的唯一解

(23)

(24)

因此，前12个参数项的辨识公式为

(t1,t2,t3,t4,t5,t6,t7,t8,t9,t10,t11,t12)=

(25)

式中：x+i、x-i分别为向量X+、X-的第i个元素。

当试验平台输出某一绕重力方向的纯定轴转动时，外壳的线加速度为零矢量；另外，还可以推导出姿态矩阵的逆矩阵

(26)

式中：θ为传感器外壳定轴旋转的角度。

此时，输入项可以分别表示成

(A1,A2,A3)=(-g,0,0)

(27)

(28)

将式(27)、(28)代入 (18)，提取所有包含参数n的项，并剔除输出轴向力为拉力的支链数据，整理可得：

(29)

式中：[·]3对应第3组辨识实验数据。

至此，已经构建了并联式六维加速度传感器全部解耦参数的辨识算法，其辨识流程如图3所示。

图3 解耦参数的辨识流程

图3显示：

(1) 并联式六维加速度传感器的试验平台除了要求能够输出六维复合运动外，还要求独立输出沿空间某个方向的纯线运动以及绕重力方向的纯角运动。

(2) 辨识并联式六维加速度传感器的13个参数项，至少需要3组实验数据，对应于辨识流程的三个步骤。其中，前两步辨识t1～t12，第三步辨识n。

(3) 辨识算法中，前两步的辨识误差直接影响第三步的辨识精度。考虑到实验次数越多则数据噪声源越多，故选取同一次纯线运动实验在两个不同时刻的采样值分别作为前两步的输入、输出数据，这有利于降低辨识误差。

2.3 辨识算法的扰动分析

实际辨识实验时，组合式标准加速度传感器存在横向灵敏度效应和尺度效应，影响输入项精度；待辨识传感器一定程度上受到电磁场等外界不确定因素的干扰，影响输出项精度。也就是说，辨识方程(19)中的A、U均不可避免地存在扰动，不妨将对应的扰动分别记作δA和δU。显然，这两类扰动项将会导致辨识出的参数项出现偏差δX。此时，式(19)转变成

(A+δA)(X+δX)=U+δU

(30)

由式(19)、(30)可得

δX=(A+δA)-1(δU-δAX)

(31)

式(31)等号两边同时取2-范数，并运用算子范数的相容特性，整理可得：

(32)

式中：I为单位矩阵。

令

(33)

式中：cond2(·)表示矩阵的“2-条件数”。

将式(33)代入式(32)

(34)

式(34)反映了并联式六维加速度传感器参数项的相对误差与输入、输出项的扰动之间的映射关系，且后两者对前者的影响程度可以通过输入矩阵的“2-条件数”指标来衡量，表现为条件数越大则影响越严重。因此，在数据扰动不可避免且大小、符号不能确定的情况下，欲最大程度地降低参数辨识误差，理论上应该选取矩阵条件数最小时的输入项。

由条件数的性质可知，若矩阵A非奇异，则：

cond2(A)≥1

(35)

将式(33)展开

(36)

式中：λmax(·)、λmin(·)分别为对应矩阵的最大、最小特征值。

当A为正交矩阵时

ATA=I

(37)

将式(37)代入式(36)

cond2(A)=1

(38)

结合式(19)、(34)、(35)、(38)可知，当并联式六维加速度传感器的输入项矩阵为正交矩阵时，其条件数为最小值，对应的辨识方程呈现“良态”。

假设k为任意正实数，A为正交矩阵，根据算子范数的齐次性，可得

cond2(A)=1

(39)

结合式(20)、(21)、(22)、(39)可知，纯线运动辨识实验的两组输入数据应分别设定为

[A1]1=[A2]1=[A3]1=k(unit)

(40)

[A1]2=[A2]2=[A3]2=-k(unit)

(41)

式中：(unit)表示1个单位的线加速度量纲。

将式(38)、(39)代入式(34)并整理，得到参数辨识的误差界

(42)

这表明，当输入、输出数据均存在扰动时，若选取式(40)、(41)所示的特征运动为输入量，则辨识出的参数项稳定可靠。

3 仿真及试验验证

3.1 虚拟样机仿真

在ADAMS中建立并联式六维加速度传感器的虚拟样机，如图4所示。其中，表现为二力杆特征的支链用无质量的弹簧代替，其两端通过球铰链分别与质量块和外壳相连接。

图4 并联式六维加速度传感器的虚拟样机

不失一般性地，对传感器的外壳依次施加四组纯线驱动，对应的前3个输入项组合列于表2中。仿真结束后，将无扰动的输入、输出数据代入图3所示辨识流程的前两步中，计算前12个参数项。

表2 纯线运动辨识的输入项

然后，在外壳上随机施加一组绕重力方向的纯角驱动，对应实验序号[5]，并将无扰动的输入、输出数据代入辨识流程的第三步中，辨识第13个参数项。各参数的辨识值及仿真值列于表3中，符号 “—”表示对应序号的实验与左端参数的辨识算法无关，t1～t12的单位为“牛顿/(伏特×千克)”，n的单位为“mm”。

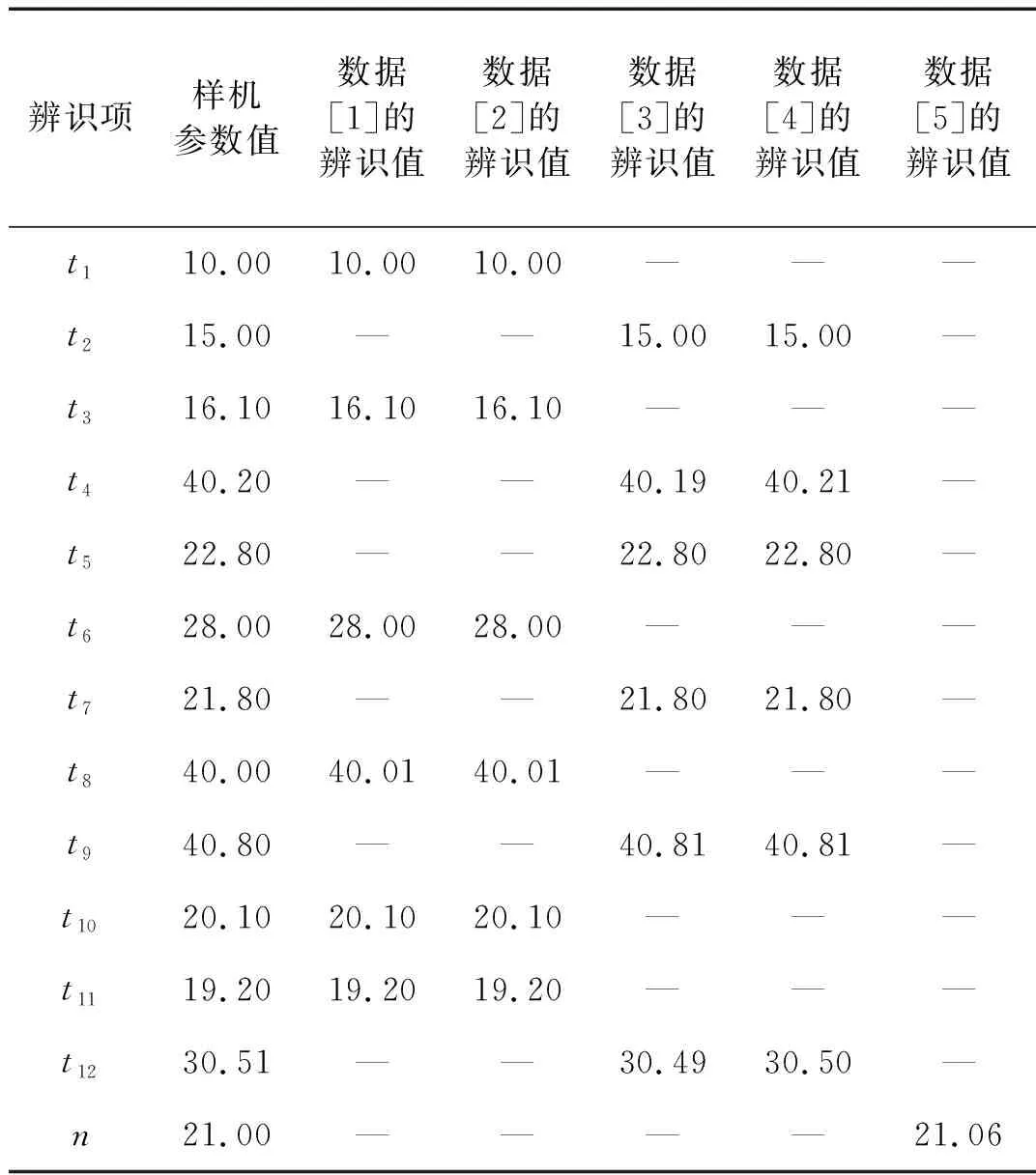
表3 解耦参数的无扰动辨识结果

结果表明，在输入项和输出项均无扰动的情况下，只要借助于3组实验数据就能够真实地还原出并联式六维加速度传感器的参数项，验证了辨识算法的正确性。表3中部分参数的辨识值和虚拟样机值之间存在微小偏差，这主要是ADAMS内核算法的积分误差和计算机的浮点数运算造成的。

最后，将实验[1]和[3]组合、[2]和[4]组合，同时在输入、输出数据中添加一系列的随机扰动，并基于辨识算法计算参数值，结果如图5所示。其中，横坐标、纵坐标分别表示测量数据的相对误差(扰动)和参数项的相对误差。

图5 扰动情况下的参数辨识误差

结果显示，非最优输入时的参数辨识值对输入、输出项扰动的敏感性和依赖程度比最优输入时的更严重，验证了扰动模型的正确性。另外，数据还显示，当外界扰动不超过1%时，并联式六维加速度传感器的参数辨识误差能够控制在0.88%之内，这与式(42)推导出的误差界完全吻合。

3.2 实物样机试验

加工制作了六维加速度传感器及其试验平台的实物样机，如图6所示。将待辨识的传感器和标准的惯性测量单元(型号为GINS100，含陀螺仪)安装固定在试验平台上感应相同的正弦加速度运动。

图6 六维加速度传感器的实物样机试验

Fig.6 Real physical prototype experiment of six-axis accelerometer

通过控制器驱动试验平台，并参照式(40)、(41)、(29)的结果提取出三组最优的试验数据。将预处理后的输入、输出数据代入辨识算法中，辨识13个参数项。进一步地，将运用本文算法以及“四步法”得到的辨识值代入解耦方程(4)～(9)中，求解六维加速度。分别计算它们与GINS100的输出值在1分钟内的相对误差，对比结果如表4所示。

数据显示，相对于“四步法”而言，本文所提算法的辨识精度更高，而且测量时间越长，优势越明显。另外，由于前者需要的有效实验数据远远多于后者(仅三组)，故本文算法的计算效率也更高。样机实验结果进一步验证了六维加速度测量中采用“低成本、无陀螺、单质量块”方案的可行性，参数辨识后，并联式六维加速度传感器的精度和效率均能满足微细切削加工、跌倒检测、组合导航等场合的应用要求。

表4 六维加速度传感器的样机试验误差

值得一提的是，由于多输入、多输出量之间的强非线性耦合特性，六维加速度传感器本身不存在线性度、横向灵敏度等传统意义(单维传感器)上的性能指标，故本文不对此进行讨论。

4 结 论

(1) 通过输入项的坐标反变换，并联式六维加速度传感器的解耦方程可以表达成非齐次线性映射的结构，且参数项的个数为13。输入项对参数项的依赖程度可以解析化为影响系数矩阵的范数，从该指标看，支链的刻度因子和质量块的边长越大越好，质量块的质量越小越好。

(2) 欲辨识上述参数项，至少需要3组有效的驱动输入，分别对应输入项均为正值、均为负值的纯线运动和绕重力方向的定轴转动。

(3) 不确定性扰动对辨识方程解的影响程度取决于方程组自身的性态，表现为输入矩阵的“2-条件数”越小，则参数解的相对误差界越小。

(4) 当扰动不超过1%时，采用最优输入驱动时的辨识误差值最小，为0.88%；实验室条件下，实物样机在1分钟内的测量误差为8.42%，精度、效率均明显优于文献[13]。欲进一步提高解耦参数的辨识精度，可以考虑通过剖析输入、输出项之间的协调关系或者提高试验平台的运动稳定性，以补偿辨识方程中给定项的测量误差，该类问题将另文研究。