非对称双激振器振动同步传动

顾大卫， 刘云山，2， 张居乾， 闻邦椿

(1. 东北大学 机械工程与自动化学院， 沈阳 110819； 2. 辽宁轨道交通职业学院， 沈阳 110023)

同步现象在生物、物理、工程及技术领域都发挥着及其重要的作用。研究同步的历史可以追溯到1665年，Huygens发现了钟摆的同步现象，并作出了相应的解释。近年来，学者们在机械系统的同步理论上做出了大量的理论探讨和试验研究，文献[1- 4]为其中的一些代表。

在工程技术领域，激振器的自同步原理广泛应用于各大工程、企事业单位当中，极大地促进了社会生产力的发展。例如，自同步振动输送机、自同步振动筛分机等。在自同步原理的应用中，有一种特殊的同步运转方式，即当两个或多个激振器同步运转过程中，断掉一个或多个(数量上少于激振器的总数)激振器的电源，断电激振器仍然能够跟随带电激振器保持同步运转，不同的是相位差会相对有些许变化，这种现象称为“振动同步传动”。此概念是闻邦椿等[5]于1984年首次在国际上提出。Xiong等[6-7]从能量传递的角度对其已经有所讨论，有关振动同步传动的过度过程也已通过数值方法给予阐释。然而，有关电机特性和系统的频率俘获及试验上的进一步验证和分析却比较缺乏。

本文以双机驱动同向回转超远共振振动系统(即系统的运转频率是其固有频率的3倍以上)的两个不对称放置的激振器同步为例，从系统耦合动力学特性角度进一步加以阐释和完善，并通过一些数值仿真和实验来验证其振动同步传动机理。

1 系统动力学模型和运动微分方程

图1为系统动力学模型，两个同向回转的激振器安装于主刚体上，主刚体通过弹簧与基础相连，两个激振器分别由两台感应电机驱动。整个系统展现出三个自由度，x,y和摆动ψ，激振器1,2分别绕各自旋转轴转动，以φ1和φ2表示。

利用拉格朗日方程，可得系统运动微分方程为

(1)

其中

J0i=mir2+j0i,i=1,2

式中：fdi,i=1,2为电机i的轴阻尼系数；le为系统绕质心当量回转半径；kx,ky,kψ为x,y和ψ方向的弹簧刚度；fx,fy,fψ为x,y和ψ方向的阻尼系数。

2 振动同步传动的同步性判据及稳定性判据

设系统稳态运行时两个激振器转动的平均相位及相位差为φ和2α，则有

φ1=φ+α,φ2=φ-α

(2)

设平均角速度为ωm0，根据文献[8-11]，得系统运动微分方程(1)的稳态响应解为

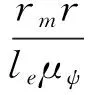
(3)

其中

设θc称为广义动态对称角[12]，其表达式如下

(4)

并引入下列无量纲参数

ρ1=1-Wco1/2,ρ2=1-Wco2/2

根据文献[9]，将系统运动微分方程(1)整理，并写成矩阵形式

(5)

其中

2.1 实现振动同步传动的同步性判据

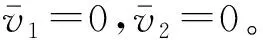
(6)

其中

式(6)中，TC为系统的频率俘获力矩，也称为广义动态对称力矩；TRi为电机i的输出残余力矩；TD为两电机当量有效输出力矩之差[14]。

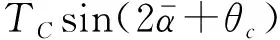
|TC|≥|TD|

(7)

式(7)为振动系统实现同步运转的同步性判据，频率俘获力矩TC的大小由系统结构参数和电机的同步转速两方面因素决定。

根据文献[9]，可得到两个激振器在振动同步传动状态下的力矩平衡方程为

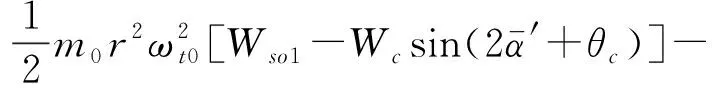
(8)

2.2 振动同步传动状态的稳定性判据

当两个激振器已经处于同步状态且稳态运转时，切断电机2的电源，式(5)中的Te02=0,ke02=0，得到振动同步传动状态下的频率俘获方程

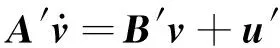
(9)

其中

(10)

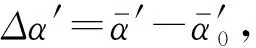
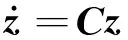
(11)

其中

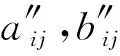
λ3+c1λ2+c2λ+c3=0

(12)

其中

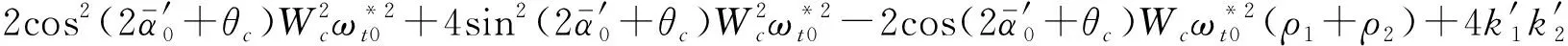
由Rourh-Hurwitz准则[15]可知，当矩阵C的特征方程(12)满足

c1>0,c3>0,c1c2>c3

(13)

时，平凡解z=0是稳定的。式(13)可进一步整理成

H0>0,H1>0,H3>0,H1H2>H0H3

(14)

H0<0,H1<0,H3<0,H1H2>H0H3

(15)

(16)

根据式(14)，得H3>0，有

(17)

3 数值分析与试验

图2为双机驱动振动同步试验台，对应图1所示力学模型，系统结构参数如下：

β1=90°，β2=140°，r=0.05 m，m1=m2=m0=4 kg，M=330 kg，l01=0.183 m，l02=0.285 m，Jm=17.85 kg·m2，le=0.234 m，rl1=rl2sinβ2，rl1=0.782，rl2=1.218，rm=0.012，kx=190.87 kN/m，ky=150.26 kN/m，kψ=20.65 kN/rad，fx=0.32 kN·s/m，fy=0.32 kN·s/m，fψ=0.28 kN·s/rad，f1=f2=f3=0.002，ξnx=ξny=ξnψ=0.07。两台电机型号相同，同向回转，型号为VB-326-W(380 V，50 Hz，6-pole，Y-连接，额定电压0.82 A，额定转速950 r/min，额定功率0.2 kW，激振力0～3 kN，绝缘等级IP54)。

图2 双机驱动振动同步试验台

3.1 数值分析

在数值分析中，为了匹配试验系统参数，设激振器1的回转中心在通过质心o的y轴上，且有：β1=90°，β2=140°，l1=l2sinβ2，rl1=rl2sinβ2。

在式(7)中，可以看出影响系统实现同步的主要参数为Wsoi和WC，是无量纲参数rm,rli,μx,μy,μψ和γx,γy,γψ,βi的函数。在远共振系统里，μx,μy,μψ及γx,γy,γψ变化很小，因此，主要研究rm,rli,βi,i=1,2对系统频率俘获的影响，设rl2≥rl1，β3=π-β2。两相同电机驱动两相同偏心块时，有

(18)

式(16)可以简化为

WC≥|(Wso1-Wso2)/2|

(19)

图3(a)是β1=β3=0°条件下频率俘获区域，且由式(19)得知无量纲参数rm对频率俘获没有影响。这里rl1rl2平面被分成三个区域：I，II和III，其中区域I和区域III能够实现频率俘获。在区域I中，稳态相位差稳定在2α∈(π/2,3π/2)，在区域III中，稳态相位差稳定在2α∈(-π/2,π/2)。

图3(b)是βi≠0°(i=1,3)且β1+β3∈(0,π/2)条件下的频率俘获区域，其中

Wcc≈rm[2-rl1rl2cos(β1+β3)]，

Wcs≈-rm[rl1rl2sin(β1+β3)]

(20)

当βi≠0°(i=1,3)且β1+β3∈(π/2,π)时，Wcc≥0恒成立，稳态相位差稳定在2α+arctan(Wcs/Wcc)∈(π/2,3π/2)。

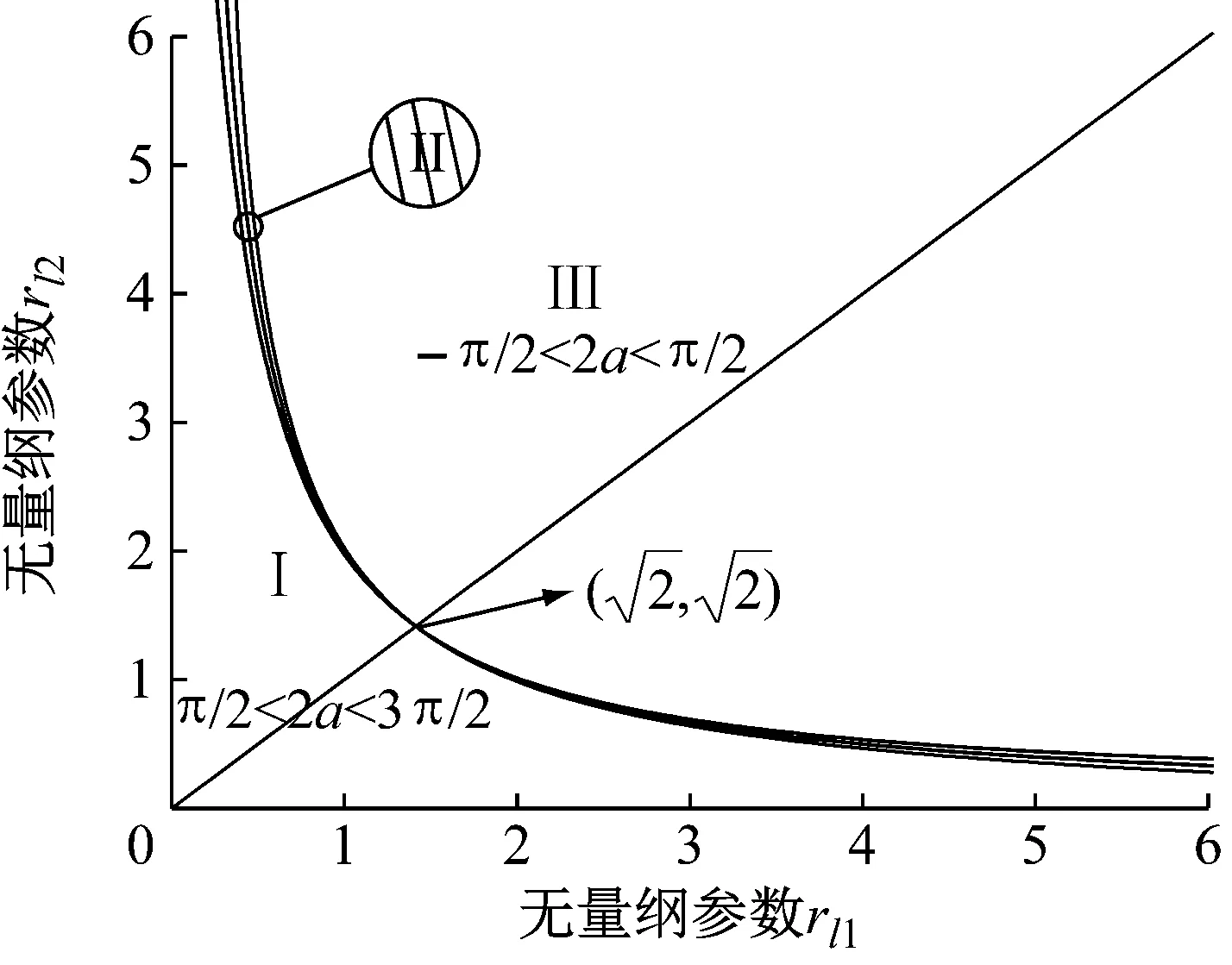
(a) β1=β3=0°

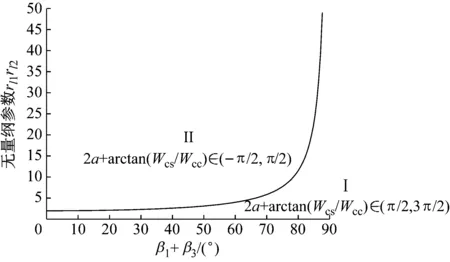
(b) β1+β3∈(0,π/2)

由式(4)可知，系统广义动态对称角θc的近似计算值如图4所示，广义动态对称角对应于振动系统平均振动能量最小值点[16]。

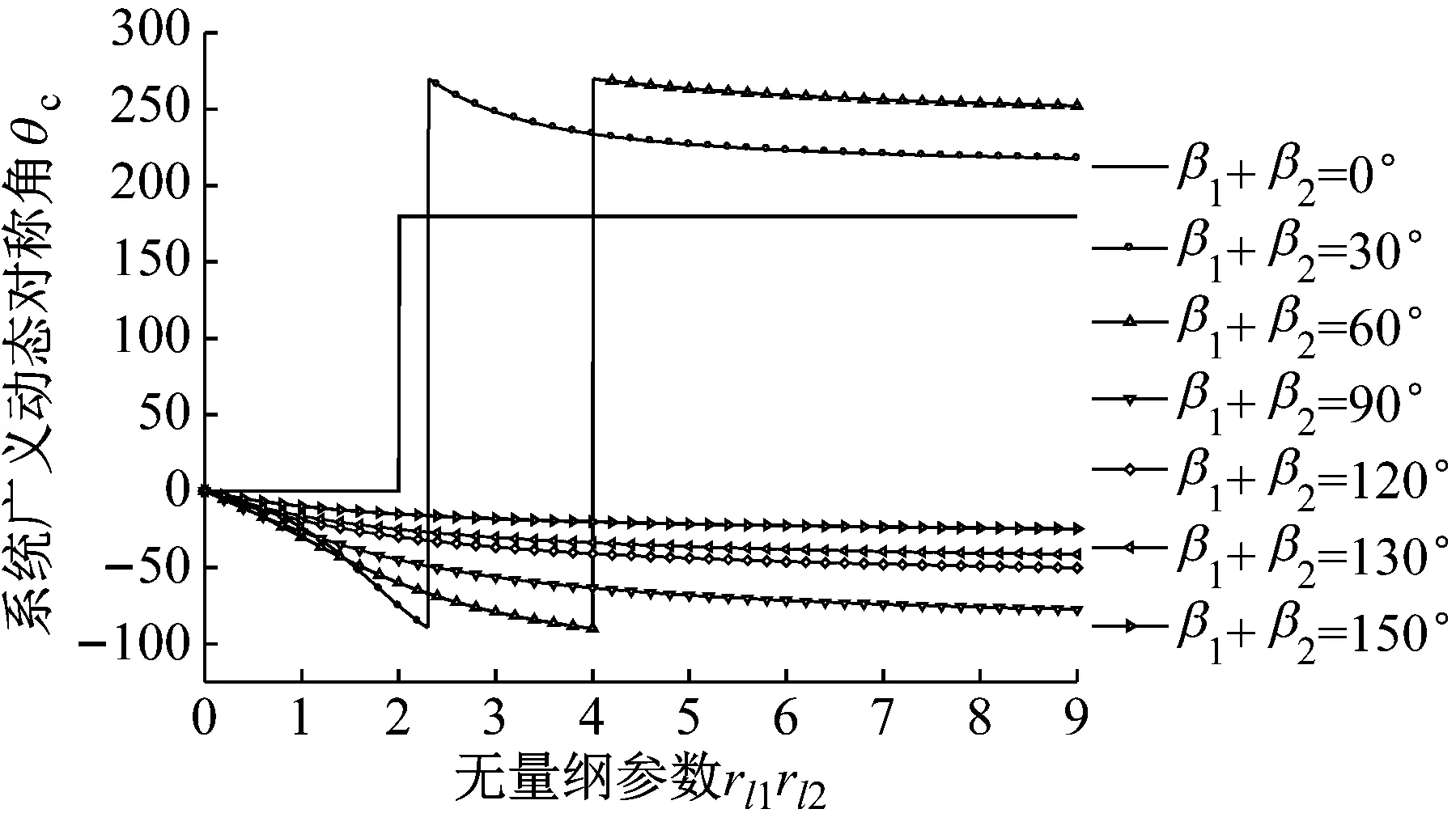
图4 系统广义动态对称角θc

系统的同步起源存在于系统负载耦合中的广义动态对称特性，因此负载耦合中激振器之间的频率俘获力矩也称为广义动态对称力矩，其限制相位超前激振器转速的升高及相位滞后激振器转速的下降，使得激振器之间的相位差接近系统广义动态对称角使得系统实现同步运转。

由式(6)及稳定性判据(17)得知，当选择两台一样性质的电机时，两个激振器之间的相位差2α的近似计算值如图5所示。

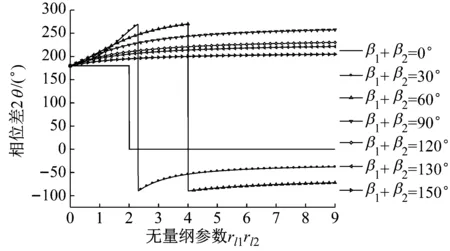
图5 2α近似计算值

根据式(3)及图5中2α近似计算值，汇总了振动系统在不同结构参数下的运动形式，如表1所示。

表1中，当结构参数接近对称时(β1+β3=0°)，由两个激振器同步运转所激发的系统的运动形式为圆周运动(rl1rl2>2)和绕质心o的摆动运动(rl1rl2<2)。当0°<β1+β3<180°时，所激发的系统运动形式为摆动运动和圆周运动共存。当β1+β3=180°时，所激发的系统运动形式为摆动运动。可以看出，当振动系统中各个激振器之间的相位差稳定在某特定值附近时，会使系统实现某种特定的运动形式。

表1 振动系统的运动形式

在表1中，当系统的结构参数接近于对称时(β1+β3=0°)，由两个激振器同步运转所激发的系统的运动形式为圆周运动(rl1rl2>2)和绕质心o的摆动运动(rl1rl2<2)。当0°<β1+β3<180°时，系统运动形式为摆动运动和圆周运动共存。当β1+β3=180°时，系统运动形式为摆动运动。可以看出，当振动系统中各个激振器之间的相位差稳定在某特定值附近时，会使系统实现某种特定的运动形式。

综上所述，在系统同步性判据和同步状态的稳定性判据都满足的条件下，振动系统会选择下列三种运动形式之一：圆周运动，摆动运动，圆周运动和摆动共存。在工程设计中，为实现合理有用的圆周运动，应使β1+β3=0°且尽量增加l01,l02的长度。

Zhang等[11]研究了双激振器对称分布情况下的系统振动同步及振动同步传动，通过对比，可以得出系统结构对称性越好，两激振器相位差趋向-θc的趋势就越好。

3.2 试验分析

试验开始时，两台振动电机同时以电源供电，通过变频器控制在40 Hz下工作。每台振动电机的偏心块质量可通过调整其偏心块夹角大小来选择，本试验中将两个偏心块质量调整为相同：m1=m2=m0=4 kg。

试验采样时间80 s，40 s处切断电机2的电源，采样频率1 024 Hz。

如图6所示，在开始通电的一段时间内，两台电机均以相同电源供电，由于两个激振器的转动惯量接近相同，因此其角加速度也接近相同。在约10 s处，两台电机的角速度与相位差达到稳定状态，此时同步转速n1≈797.9 r/min，相位差2α≈188.6°，此结果与图3(b)和图5基本一致。

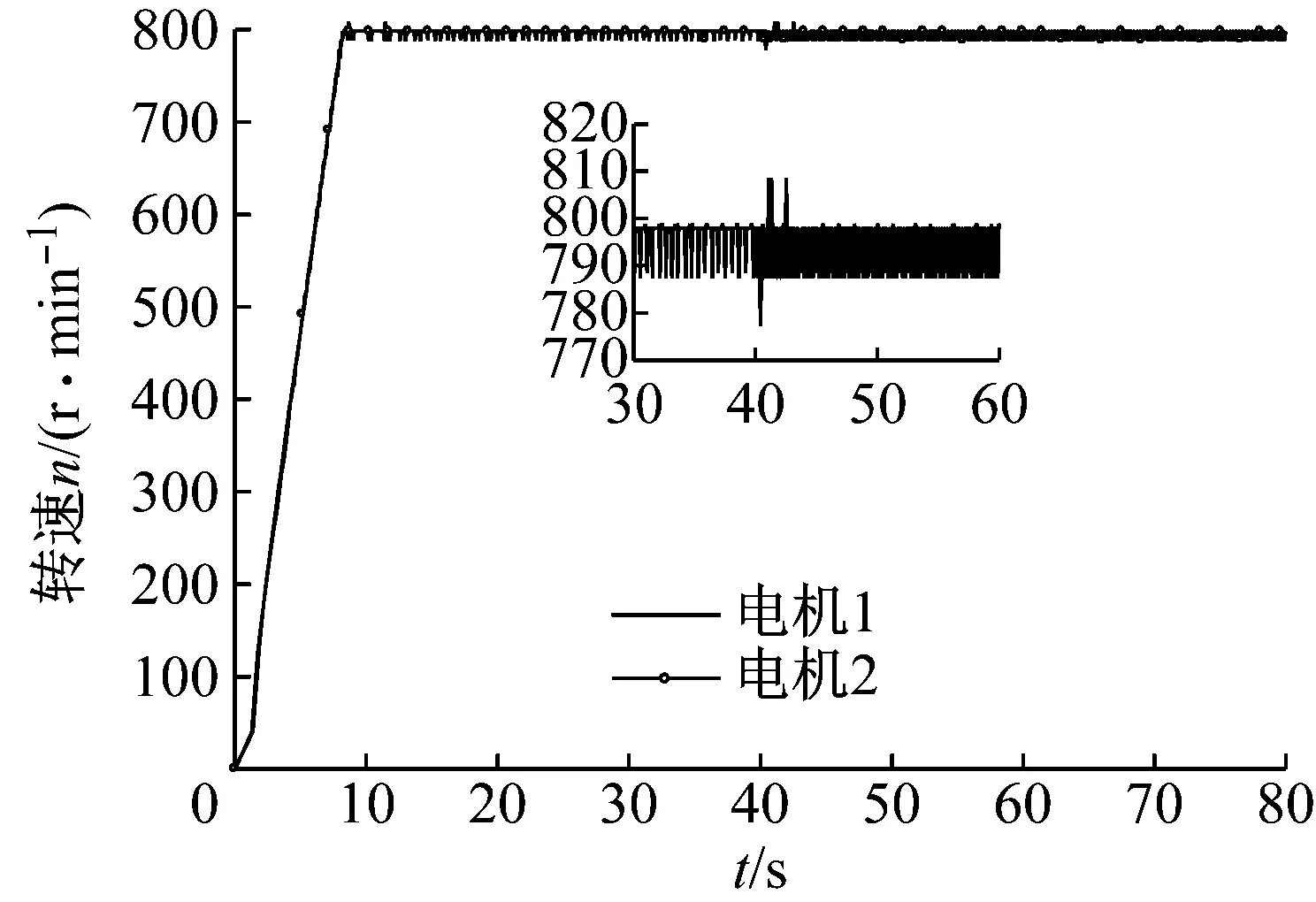
(a) 两电机转速

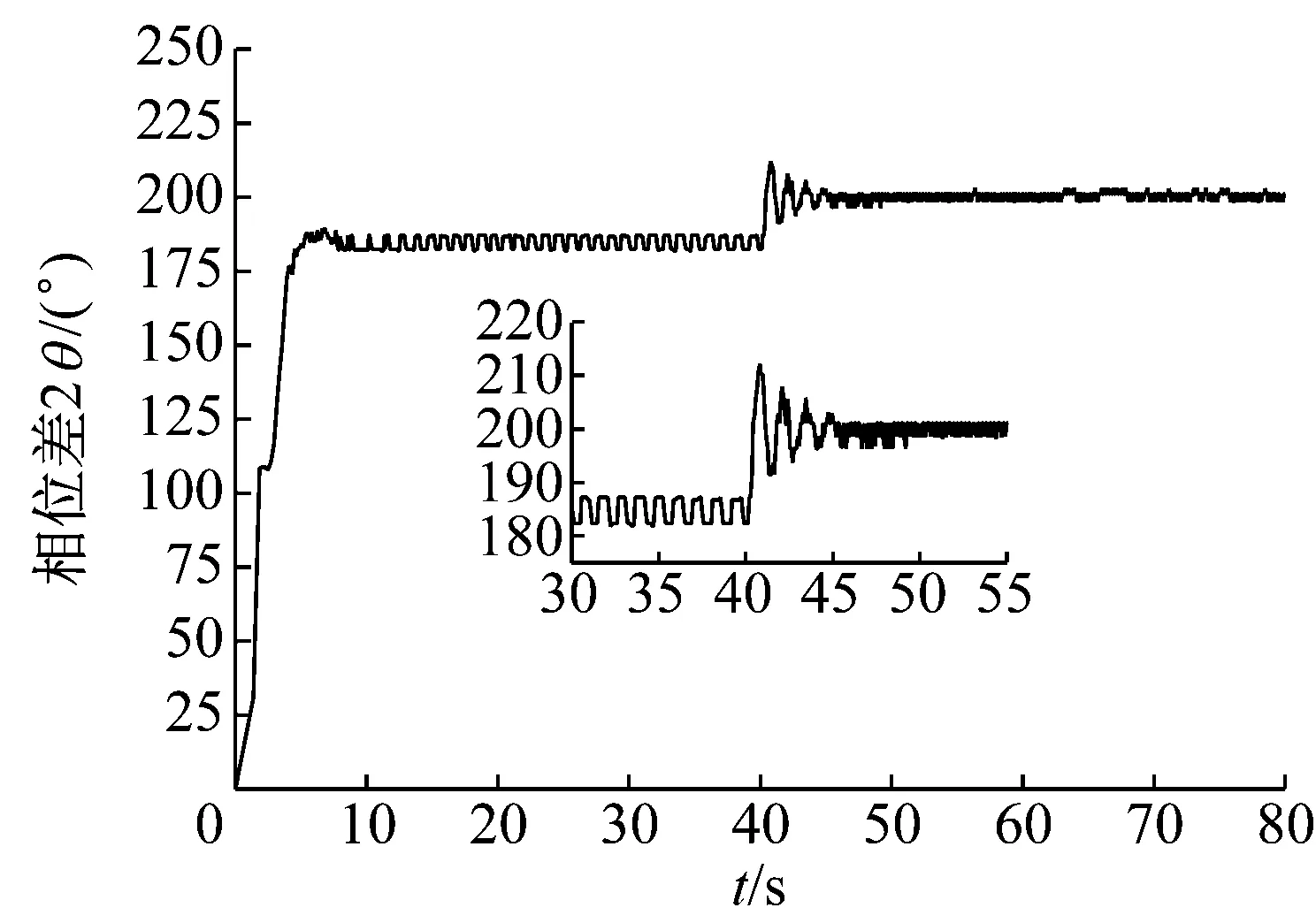
(b) 两激振器相位差(2α=φ1-φ2)

图7和图8为供电频率40 Hz下高速摄影机记录的电机2断电前后系统稳态时的回转相位图，以两个激振器的回转中心连线为基准线，相位误差在0°～2°。如图7所示，电机2断电前系统稳态时两个激振器的相位差为187.9°～190.9°。如图8所示，电机2断电后系统稳态时即系统实现振动同步传动时两个激振器的相位差为206.2°～210.7°。此结果与图5和图6(b)基本一致。

(a) φ1≈205.7°,φ2≈15.6°,φ1-φ2≈190.1°

(b) φ1≈299.4°,φ2≈110.7°,φ1-φ2≈188.7°

(c) φ1≈393.6°,φ2≈203.8°,φ1-φ2≈189.8°

(d) φ1≈491.8°,φ2≈300.9°,φ1-φ2≈190.9°

(e) φ1≈586.5°,φ2≈397.7°,φ1-φ2≈188.8°

(f) φ1≈681.3°,φ2≈492.4°,φ1-φ2≈188.9°

(a) φ1≈227.8°,φ2≈21.6°,φ1-φ2≈206.2°

(b) φ1≈321.0°,φ2≈114.7°,φ1-φ2≈206.3°

(c) φ1≈417.4°,φ2≈207.5°,φ1-φ2≈209.9°

(d) φ1≈515.1°,φ2≈306.4°,φ1-φ2≈208.7°

(e) φ1≈609.1°,φ2≈401.5°,φ1-φ2≈207.6°

(f) φ1≈703.2°,φ2≈495.6°,φ1-φ2≈207.6°

将试验系统结构参数及试验结果代入系统振动同步传动状态下的稳定性判据式(16)和式(17)中，如表2所示，可知振动同步传动状态下的稳定性指数都大于零，理论上说明系统稳定，与试验结果相符合，验证了所用理论方法的有效性。

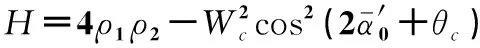
表2 电机2断电后系统振动同步传动状态下的稳定性

4 结 论

(1) 利用时间双尺度法，获取系统的频率俘获方程，给出了系统实现振动同步传动的同步性判据及同步状态的稳定性判据。此判据可以为双机同向回转自同步振动机实现振动同步传动提供了理论依据。

(2) 针对当前的动力学模型，要想实现振动同步传动，首先必须实现双机同时供电条件下的同步运转，产生频率俘获力矩，以保证系统在振动同步传动过程中进行扭矩传递，使得系统得以继续保持同步运转。

(3) 对于当前的力学模型，当系统的结构参数接近对称时(β1+β3=0°)，由两个激振器同步运转所激发的系统运动形式为圆周运动(rl1rl2>2)和绕质心o摆动运动(rl1rl2<2)；当0°<β1+β3<180°时，由两个激振器同步运转所激发的系统运动形式为摆动运动和圆周运动共存；当β1+β3=180°时，由两个激振器同步运转所激发的系统运动形式为摆动运动。因此在同步性判据和稳定性判据都满足的条件下，振动系统会选择下列三种运动形式之一：圆周运动，摆动，圆周运动和摆动共存。在工程设计中，为实现合理有用的圆周运动，应使β1+β3=0°且尽量增加l01,l02的长度。

(4) 电机2断电前系统稳态时的同步转速为n1≈797.9 r/min，相位差2α≈188.6°。振动同步传动状态下的同步转速n2≈787.4 r/min，相位差2α′≈206.7°，与电机2断电前相比，同步转速下降，相位差增加，但断电前后相位差的变化及转速的变化不大。频率俘获力矩通过调整两个激振器之间的相位差来达到系统能量的分配与再分配，从而保证了系统的平衡稳定运转。

(5) 由于电机2断电前后系统稳态时两个激振器的同步转速和相位差变化不大，因此振动系统的主要运动形式保持不变，即圆周运动和摆动，从而说明了系统实现振动同步传动对系统的运动形式影响微小。而振动系统的摆动对工业生产毫无意义，在工程上，一般可以通过调整两台电机在机体上的位置从而使得β1+β3=0°，rl1rl2>2，从而实现对工程有用的近似圆的圆椭圆轨迹。利用该运动形式可以设计振动输送机等振动设备。