博弈方法在进料抽样方案选择中的应用分析

(上海理工大学 上海 200000)

关于抽样，是质量工作者都熟悉的一个方法，其原理是基于成本的考量，用所随机抽取出来的子产品的表现来代表整个母本的表现，用AQL来表示。AQL代表抽样方案，表示来料如果质量水平(不良率)为某一方案时，来料会以相应的概率被接收。

按照业界常用的计数抽样表GB2828(同ANSI/ASQ Z1.4)为例，以双方约定的抽样表，当AQL=0.65时，抽检80pcs的标准是1收2退，对产线造成的影响是必须容忍每批次AOQ(Average Outgoing Quality，即平均检出质量)约有0.625%的原材不良率。

通常，AOQ的值会随来料不良率的升高而升高，然后降低(因为在不良率达到一定程度时被判退的风险，经筛选剔除出不良品后，它的总体不良率反而降低了，这个不良率的上限值即为AOQL，平均检出质量上限)。

很多时候，这样的质量表现不能够被产线接受，对IQC部门的影响是显而易见的：子产品的表现符合约定的质量水准，则批收，即使知道这种接收含有相当程度的材料质量风险。这样，它必然要受到产线的指责。

业界一般用OC曲线(Operating Characteristic Curve，即抽样特性曲线)[1]来表示对一个给定的过程质量时，各抽样方案预期的可接收的批的百分数。OC曲线是建立在概率论和数理统计基础之上的抽样检验特性曲线，利用它可以较好地确定合格质量水平、生产与消费方风险和检验水平。

每个抽样方案都有自己的OC曲线，批品质越好其接收概率会越高、批品质不好时接收概率会越低、批品质合格时有高接收概率，但理想OC曲线即使全检也达不到。如图1所示OC曲线图。

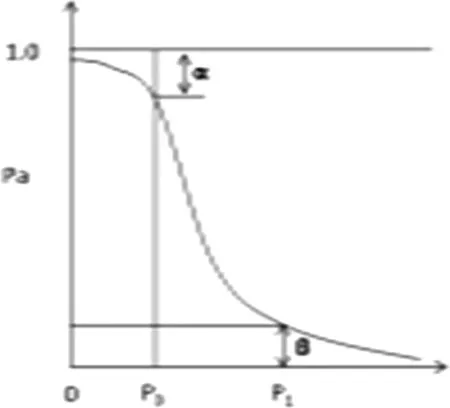
图1 OC曲线图

P0=AQL，相当于接收概率为(1-α)时的批不合格率，α取5%或1%；

P1=LTDP(消费者不满意的送验批所含有的最少不良率)，相当于接收概率为β时的批不合格率，β通常取1%～10%。

抽样检验是部分代替总体，必然会产生风险，是无法消除的。当批质量符合要求却不被接收时生产方承担的风险，我们称之为生产方风险，即α风险；而批质量不符合要求却被接收时使用方承担的风险，我们称之为使用方风险，即β风险。

两种风险是截然对立的，或者风险落在生产方一边，或者转嫁到使用方一边。因此，供需双方对AQL的选择，在业界一般遵循传统的选择方式：比较重要的质量水准，AQL要求会小些；相对不那么重要的参数，AQL的要求会大些。

但是当AQL要求严格的话，必然要使得生产方一方对质量的投入要大一些，相应地质量成本也会变高。这样的话，使用方对材料的采购成本势必要上升；但是当AQL不足以满足生产部门的要求时，最终伤害的是做供需双方的互利关系。两种风险的选择，其实就是一个动态博弈的过程。

为了达到双方的最佳质量成本水平，根据“帕累托最优”原则，博弈双方必须寻找到一个最佳的AQL水准，来同时满足供应与生产的最优条件。博弈学上的“纳什均衡”很好地阐释了这个问题。

所谓“纳什均衡”，是假设有n个局中人参与博弈(此案为供应方与生产方两个)。如果某情况下没有任一参与者可以在独自行动中增加收益(在其它方不愿意改变其策略时)，即为纳什均衡，它的实质上是一种非合作博弈。

在应对α、β风险的选择中，无论供、需哪一方主动进行质量检验加严控制(检验)，都可以达到提升质量的目的，当然，相对的成本投入，还是能够获得一定的质量回报的。只是根据OC曲线，理想的品质状态即使全检也达不到。这样，达到一个什么样的质量水准就形成供需双方的博弈。

假设对供需双方而言，一方加严检验，会带来己方成本一定程度的增加，但同时会减少不合格品所带来的维修或报废或索赔成本的减少。是否由某一方或双方共同承担这种检验成本的增加，这样就形成了基本的博弈矩阵。

如果生产方单方面进行加严检验，将会有n1的成本增加(含少量流到产线维修的费用)；如果生产方与使用方同时加严检验，将会有n2的成本增加(几乎没有不良品需维修)；如果使用方单方面加强检验，将会有n3的成本增加，但生产方只需负责n4的不良交换成本；如果双方同时保持现状，则有很大概率分别承担n5和n6的成本(对使用方有承担AQL内风险的义务，而生产方则需额外负担不良维修导致的急剧上升的维修成本)。由此形成了生产方与使用方的博弈矩阵，见表1。

表1两种风险的博弈矩阵

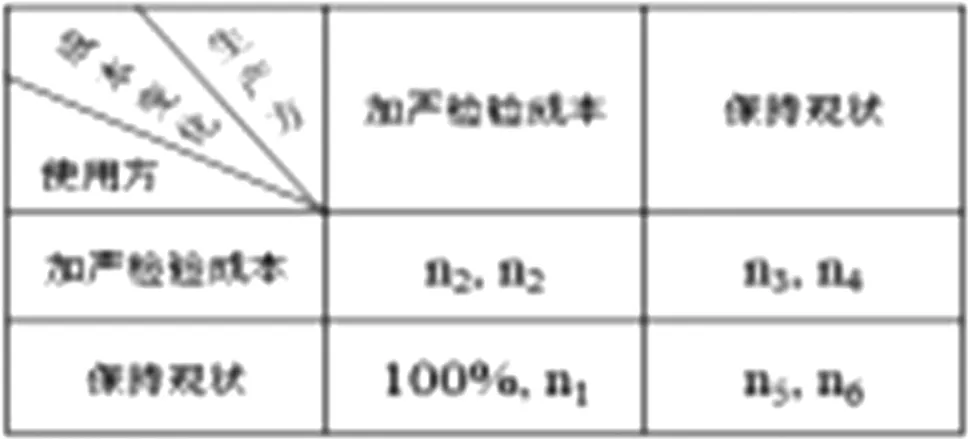
从质量控制的角度，对比不同方案下的质量成本，可以迫使供需双方在进行相应的质量成本核算后，得出对其最有利的质量保证方案。对生产方来说，根据自身产品的质量水平确定适当的抽样方案，在增加检验成本和因不良材料而受到的惩罚之间作一个最合乎利益的选择是必要的；对使用方来说，通过适当的统计分析，与生产方达成最佳的质量成本，是一个双赢的过程。