基于组合学的茧丝落绪分拆模拟与分析
2019-01-22黄继伟宁晚娥左保齐
黄继伟, 宁晚娥, 张 锋, 左保齐
(1. 广西科技大学 生物与化学工程学院, 广西 柳州 545006; 2. 苏州大学 纺织与服装工程学院,江苏 苏州 215006; 3. 现代丝绸国家工程实验室(苏州), 江苏 苏州 215123)
缫丝是将若干蚕茧的茧丝离解并合成一定规格生丝的加工过程[1]。在此过程中,受蚕茧本身的品质、缫丝前处理和缫丝工艺技术等因素的影响,1根完整的茧丝通常被分拆成若干解舒丝段参与并合成生丝[2-4],且这种茧丝的分拆程度和规律对缫丝的产质耗存在显著影响,包括解舒率、解舒丝长和落绪次数等能反映茧丝分拆程度的指标,在缫丝工艺研究中被广泛地关注[5],而这些指标的概率分布及统计特征作为可揭示茧丝分拆规律的工具已被深入地研究和报道[6-8]。其中,白伦等[9-11]将1根连续的茧丝离散化,假设茧丝上的落绪只可能发生在有限的等间距的离散点上,进一步地探讨了茧丝长和解舒丝长的关系,给出了相关的概率分布及其统计特征,并设计出了模拟生成解舒丝段的方法。这种方法被广泛地应用于计算机模拟缫丝中,成为推动计算机模拟缫丝及缫丝系统工程研究的重要基础[12-14]。然而,基于解舒丝长概率分布模拟生成解舒丝段的方法,并不能直观地反映缫丝中1根完整茧丝分多段多次参与生丝并合的情况。
本文在茧丝离散化落绪点模型的基础上,将茧丝上的1个落绪节点子集与1种落绪分拆模式对应,并计算出1根茧丝所有落绪分拆模式的概率,进而利用逆变换取样法对该茧丝所有落绪分拆模式进行随机抽样,实现了对1根完整茧丝的落绪分拆模拟,该方法直接将1根完整的茧丝分拆成若干解舒丝段,完整保留了1根茧丝的所有数据信息,更加直观反映缫丝中1根完整茧丝分多段多次参与生丝并合,从而更加直观和易于理解,以期为计算机模拟缫丝提供新的解舒丝段模拟和生成解决方案。
1 茧丝落绪节点的落绪率
1粒蚕茧是由1根茧丝缠绕而成,若以一定长度摇取茧丝,可将茧丝在其长度方向上分成若干等长的丝段,这些丝段被称为“纤度丝”,将这些纤度丝依次称量换算后可得一系列线密度值,称为茧丝线密度序列[15]。茧丝线密度序列实质上是对连续的茧丝在其长度方向上的离散化,用来反映茧丝线密度在其长度方向上的变化情况。总体上,茧丝线密度序列符合“细-粗-细,最末处最细”的变化模式。
关于茧丝线密度序列的统计特征,白伦等[16-17]、费万春[18]和胡征宇等[19]进行了系统的研究,并提出了多种茧丝线密度序列模拟生成方法,这些方法可为计算机模拟缫丝提供无尽的“原料茧丝”数据,是计算机模拟缫丝系统设计的前提和基础。然而实际缫丝中,处于缫丝状态的茧丝可能发生断裂,即产生落绪现象,导致1根完整的茧丝实质上是被分拆成若干丝段参与并合成生丝的。也就是说,茧丝线密度序列并不能直接作为计算机模拟缫丝的“原料”使用,需要将茧丝线密度序列在长度方向上分拆成合理长度的解舒丝段才可使用,这就引出了茧丝线密度序列分拆的问题。
以茧丝线密度序列为基础,建立茧丝落绪节点落绪率模型是完成茧丝线密度序列分拆的前提,前人对此已有深入的研究和报道[19-20],概括如下。
1)假设1根茧丝按一定单位长度(即纤度丝长度)被分为M个纤度丝(M可看作是用正整数表示的茧丝长),而落绪只可能发生在纤度丝的端点上,除茧丝首末两端点外,茧丝上共有M-1个端点,这些端点被称为落绪节点。图1示出茧丝长M=16(纤度丝长为56.25 m,茧丝实际长度为56.25 m×16=900 m)的茧丝线密度曲线、落绪节点及其落绪率。
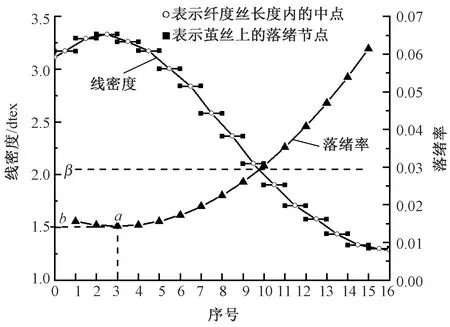
图1 茧丝落绪节点及其落绪率Fig.1 Dropping nodes and probability of bave
2)对于茧丝上落绪节点的落绪率pM,i,用一开口向上的二次曲线模型计算获得。
pM,i=kMi-a2+b(1≤i≤(M-1))
(1)
式中:a为茧丝上落绪率最小的节点序号;b为茧丝上最小的落绪率(如图1所示);kM为模型系数。
3)记茧丝上落绪节点的平均落绪率为β,即:
(2)
由式(2)可求得:
(3)
β与庄口茧丝的解舒率有关。若1个蚕茧庄口的解舒率为J,庄口平均粒茧落绪次数为ZM,则
(4)
图2为解舒率J分别是10%、30%、50%、70%、90%时的落绪节点落绪率曲线图。

图2 不同解舒率的茧丝落绪节点的落绪率曲线图Fig.2 Dropping probability of bave dropping nodes with different reelability percent parameters
4)设存在一个值C=b/β,则C被称为落绪均一度,用以表征蚕茧的煮熟程度,蚕茧煮熟程度越好,C值越接近1,各节点落绪率越趋于均等。
图3示出C值分别是0.1、0.3、0.5、0.7、0.9、1.0时的落绪节点落绪率曲线。

图3 不同落绪均一度值的茧丝落绪节点的落绪率曲线图Fig.3 Dropping probability of bave dropping nodes with different dropping uniformity parameters
5)设茧丝最小落绪率的位置a与M的比值为ρ=a/M。则ρ可用来表征茧丝落绪部位分布的类型,根据文献[20],将茧丝落绪部位分布类型分为3种,分别定义如下:
① 0≤ρ<0.4,落绪部位分布为J型。
② 0.4≤ρ<0.6,落绪部位分布为U型。
③ 0.6≤ρ≤1,落绪部位分布为L型。
图4示出ρ分别是0.187 5,0.375 0,0.562 5,0.750 0,0.937 5时的落绪节点落绪率曲线。

图4 不同落绪部位参数的茧丝落绪节点的落绪率曲线图Fig.4 Dropping probability of bave dropping nodes with different dropping position parameters
根据前述假设,式(1)、(3)可变换为
pM,i=kM(i-ρM)2+Cβ
(5)
(6)
6)若茧丝上第i个节点的落绪率为pM,i,则该节点上不落绪的概率为
qM,i=1-pM,i
(7)
2 茧丝落绪分拆模型及模拟实现
2.1 基于组合学的茧丝落绪分拆模型
假设有一个茧丝线密度序列,其长度为M,则其落绪节点数为M-1。将这些落绪节点依次编号,可得到一个落绪节点序号列表1,2,…,i,…,M-1。该列表可被看作是一个元素不重复的顺序排列的集合[22]。从该集合中任取一子集,则该子集的所包含的序号可表示茧丝在缫丝时出现落绪的断点。例如:子集{t,k}可表示缫丝时茧丝分别在落绪节点t和k处发生了落绪,其他落绪节点均未发生落绪。这里,将落绪节点序号列表集合的一个子集所对应的落绪分拆情况称为一种落绪分拆模式。
根据前述的茧丝落绪节点落绪率模型,每个落绪节点序号均有一个落绪率与之对应,即一种落绪模式产生的概率是被唯一确定的。例如:子集{t,k}所表示的事件概率为
(8)
这里将落绪节点序号列表1,2,…,i,…,M-1所形成的集合,称为母集。若计算其所有子集所对应的落绪模式发生概率,可知道其和为1。即1根茧丝上所有可能的落绪模式的概率和为1。这里用一些特例和简单情况为例进行说明,见表1所示。

表1 茧丝落绪分拆的简单实例Tab.1 Some simple examples of bave dropping partition
由表1可知,只要知道发生落绪的节点对应的序号,即可求出这种分拆模式所对应的分拆概率,而所有分拆模式的概率和为1。
对于某茧丝长M,其落绪节点序号列表1,2,…,i,…,M-1是确定的,该列表的所有子集也是确定的,因此,可以求出茧丝长为M时的所有的落绪模式以及每种落绪模式所对应的概率。根据这个概率分布,利用逆变换的方法[23]进行随机取样即可生成一种落绪模式,完成茧丝的分拆。
2.2 茧丝落绪分拆模拟系统的实现步骤
1)生成茧丝线密度序列,获取茧丝线密度序列的长度值M和序列中线密度值最小位置的索引序号a(根据二次函数落绪率模型的假设,该位置即为茧丝上落绪率最小的节点),计算线密度最小位置的索引序号a与线密度序列长度M的比值ρ。对于茧丝线密度序列的生成,可根据需要,选择阶梯式自回归模型[16]、二次曲线解析模型[17]、时变参数自回归模型[18]或拟合模型[19]进行模拟生成。
2)设置庄口解舒率J,茧丝落绪均一度参数C,根据茧丝落绪率模型,计算模型系数、所有茧丝落绪节点的落绪率和茧丝落绪节点序号列表。
3)以茧丝落绪节点序号列表为母集,计算产生其所有子集,根据茧丝落绪节点的落绪率,计算每个子集所对应的落绪分拆模式的概率,基于此,构建出以落绪分拆模式为枚举型随机变量的概率质量函数。
4)基于茧丝所有落绪分拆模式及其概率值,利用逆变换的方法[24],随机生成一种落绪分拆模式,完成茧丝线密度序列的分拆。
5)若只针对1根茧丝进行重复分拆,只需利用逆变换的方法反复对所有落绪分拆模式进行抽样即可。若需要针对1组茧丝进行分拆,则需要对该组茧丝中的每根茧丝重复步骤1)~4)。
3 茧丝落绪分拆模拟与统计分析
3.1 1根茧丝所有落绪模式的统计分析
以茧丝长M=16为例,分别设置不同的解舒率J,落绪均一度C和落绪部位参数ρ等参数,对于每种参数配置情况,首先计算产生其所有落绪分拆模式(即生成一个茧丝落绪节点集合的子集)及每种落绪分拆模式的概率,然后统计解舒丝长(一段连续未发生落绪的茧丝个数)和落绪次数的分布情况。
图5示出C=0.8,ρ=0.1875,分别设置庄口解舒率J为10%、30%、50%、70%、90%的统计情况。
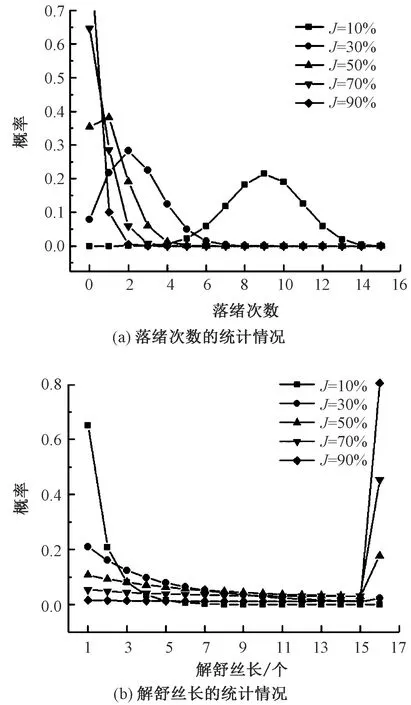
图5 不同解舒率参数时所有落绪模式的落绪次数和解舒丝长的统计情况Fig.5 Statistical overview of dropping times (a) and reelability length (b) of all dropping patterns at bave node dropping probabilities with different reelability percent parameter
由图5可知,随着庄口解舒率J的增加,茧丝落绪节点的落绪率逐渐变小,这是落绪率模型所决定的。同时,随着庄口解舒率J的增加,最大概率的落绪次数逐渐向0次偏移,即解舒率越大,茧丝发生落绪的次数越少,这也是与事实相符合的。进一步地,随着庄口解舒率J的增加,解舒丝长越长,这与落绪次数的结论可形成相互印证。
图6示出J=70%,ρ=0.187 5,分别设置落绪均一度C值为0.1、0.3、0.5、0.7、0.9、1.0时的统计情况。

图6 不同落绪均一度参数时所有落绪模式的落绪次数和解舒丝长的统计情况Fig.6 Statistical overview of dropping times (a) and reelability length (b) of all dropping patterns at bave node dropping probabilities with different dropping uniformity parameters
由图6可知,随着落绪均一度C值的增加,茧丝落绪节点的落绪率逐渐趋于均等,当C=1.0时,所有节点的落绪率完全一致。同时,随着落绪均一度C值的增大,在落绪次数几乎不发生变化,这与落绪次数受解舒率J所决定的事实相符合。进一步地,随着落绪均一度C值的增大,在解舒丝长的概率趋势从内凹逐渐变为平直。
图7示出当J=70%,C=0.8时,分别设置落绪部位ρ为0.187 5、0.375 0、0.562 5、0.750 0、0.937 5时的统计情况。
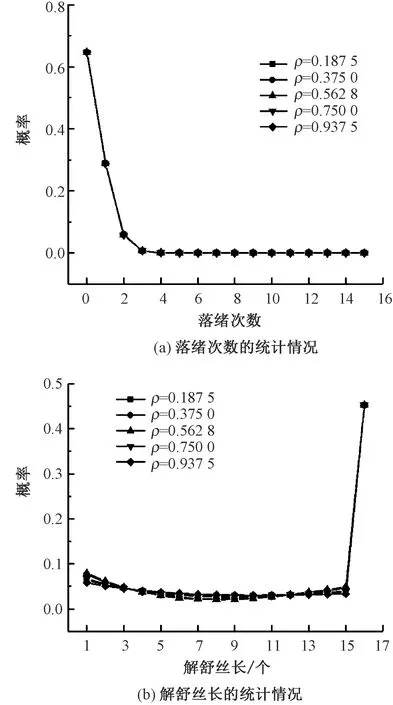
图7 不同落绪部位参数时所有落绪模式的落绪次数和解舒丝长的统计情况Fig.7 Statistical overview of dropping times (a) and reelability length (b) of all dropping patterns at bave node dropping probabilities with different dropping position parameters
由图7可知,随着落绪部位ρ的增加,最大落绪率位置逐渐向大序号的落绪节点移动,这是由落绪率模型所决定的。落绪次数与不同落绪均一度C值时的情况相同,并未发生太大的变化。随着落绪部位ρ的增大,解舒丝长的概率趋势的凹度先增大再减小。
关于解舒丝长的分布,白伦等[11]基于有序分拆模型,推导出解舒丝长与茧丝长的关系式,见式(10)~(12)。通过计算对比,其与本文方法所得结果基本一致。
(10)
(11)
(12)
3.2 对1根茧丝进行反复落绪分拆的模拟
为验证系统的稳定性和准确性,在此以茧丝长16为例,对其进行反复的落绪分拆模拟,模拟计算过程简述如下。
1)设置系统参数,包括解舒率J、落绪均一度C和落绪部位ρ。
2)对茧丝长为16的茧丝,根据所设置的系统参数和茧丝落绪节点落绪率模型,计算茧丝上所有落绪节点的落绪率。
3)以茧丝落绪节点序号为母集,生成其所有子集,并计算所有子集对应的落绪模式及其概率。
4)根据所计算的所有子集对应的落绪模式及其概率,运用逆变换法进行随机抽样,最后,统计该抽样的落绪次数和解舒丝长分布情况。
图8示出当解舒率J=10%、30%、50%、70%、90%,落绪均一度C=0.8,落绪部位ρ=0.187 5,抽样100万次时,落绪次数和解舒丝长的分布情况。

图8 茧丝长为一定值时的随机分拆模拟结果Fig.8 Result of random partition simulation at fixed length of bave. (a) Number of bave dropping times; (b) Non-broken filament length
由图8可知,茧丝长一定时,通过变换解舒率参数J获得的落绪次数及解舒丝长的分布完全模拟出了该茧丝的所有落绪模式时的情况,通过改变落绪均一度C,落绪部位参数ρ,同样可获得与该茧丝长时的所有落绪模式的相似情况,在此不再赘述。这个结果说明模拟系统是稳定的,模拟方法是可行的。
3.3 茧丝长为正态分布时的落绪分拆模拟
对于同一庄口的蚕茧,其茧丝长符合正态分布,现对此事实情况进行模拟,并分析落绪次数和解舒丝长的分布情况,过程如下。
1)设置系统参数,包括解舒率J、落绪均一度C和落绪部位ρ。
2)设置茧丝长的平均值和标准差参数,生成一组符合正态分布的茧丝长数据。
3)对于每个茧丝长数据,参照3.2节所述的步骤,随机抽样1次,并保存结果。
图9示出当茧丝长符合均值为16,标准差为3时的正态分布,解舒率J=70%,落绪均一度C=0.5,落绪部位ρ=0.187 5时,随机生成20 000根茧丝的分拆统计情况。

图9 茧丝长为正态分布时的随机分拆模拟结果Fig.9 Result of random partition simulation at normal distributed length of bave. (a) Number of bave dropping times;(b) Non-broken filament length
由图9所示的结果与白伦等[25]推导出的解舒丝长分布一致,这说明该茧丝落绪分拆模型与解舒丝段模拟生成方法是正确的。其完全适用于计算机模拟缫丝和实际制丝工程中原料茧性质与缫丝指标之间的关系研究。
4 结 论
本文在离散化茧丝落绪点模型的基础上,运用组合学理论,通过将落绪节点集合的子集与落绪模式对应,使茧丝分拆转化为获取落绪节点集合的子集,并利用离散随机变量分布的逆变换取样法,完成茧丝分拆的随机取样,实现茧丝的分拆。通过对1根茧丝所有落绪模式的统计分析、1根茧丝进行多次落绪分拆的模拟和茧丝长为正态分布时的茧丝落绪分拆模拟,确认该模型及方法符合缫丝过程的实际情况,且与前人的研究结果基本一致。而模型所提出的将1根完整茧丝一次性分拆的思路也更符合缫丝中1根完整茧丝分多段多次参与生丝并合的实际情况。
FZXB
