层状孔隙介质中局域流的相互干扰研究

邓社根，滕新保，曹旖旎，王美均

(江苏省工程勘测研究院有限责任公司地质勘查处，江苏 扬州 225000)

研究表明当纵波通过不均匀孔隙介质的时候，介质中的不均匀体会诱发局部区域孔隙压力梯度，导致孔隙中的流体在压力梯度的作用下发生耗散，这一耗散机制称之为局域流[1-3]。当这种局域流在尺度上远大于介质组成孔隙的尺度同时小于纵波传播的波长时候，称之为中观局域流。研究表明在地震频段内，中观尺度局域流是岩石表现出较强速度频散与衰减的主要原因之一[4-6]。

文献[7- 8]以Biot理论为基础，分别研究了“球状气包”模型和含气、 含水层交错排列的周期层状孔隙介质中纵波衰减与频散特征，并提出了中观尺寸下局域流带来的衰减解析式。文献[9-10]则是改进了White 理论并得到了一个低频极限下，更为精确的纵波波速。文献[11]则是引用了两种描述斑状形状的几何参数，建立了一种适用性更为广泛的解析式。文献[12]基于微观流场的考虑，利用微观BISQ(Biot/Squirt)理论，建立孔隙各向异性介质中，同时处理Biot和喷射流动机制的弹性波传播方程。文献[13-14]则是针对球状patchy模型和周期成层孔隙介质，用孔隙介质力学的方法研究了两种介质中波的衰减和速度频散；文献[15]则是在Biot孔隙介质的波动理论基础上，分析了裂隙在弹性波动作用下的“喷射流”(squirt flow)效应；文献[16]则是在周期性层状孔隙介质模型结合了宏观尺度“Biot流”和中观尺度“局域流”两种衰减诱导机制，引入了微观尺度硬币型和尖灭型裂隙“喷射流”的影响，分析了该模型在不同裂隙参数及裂隙体积含量下的纵波衰减和频散特征；文献[17-18]发展了双孔隙理论，设计了球状流体的振荡模型以描述局域流，原创地推导了格式较为简介、容易实现的波传播方程。然而，大部分现有的解析式大部分均是基于等效介质或者周期性介质，然而实际中地球岩石，其内部介质的分布特征可能与储层环境，成藏过程，孔隙结构有关。因此研究复杂介质局域流的分布更具有现实意义。

为了更好的研究复杂介质中局域流的分布，国内外学者开始通过数值模拟的方法研究不均匀体中局域流分布及其所对应的衰减和速度频散。文献[19]采用Biot孔隙弹性理论[20]进行了数值模拟，研究了局域流所造成衰减以及速度频散的变化情况。国外学者则在Masson等基础上，优化了Biot孔隙弹性理论，采用固结Biot孔隙弹性方程[21]，通过蠕变数值模拟方法研究了低频之下局域流的变化；文献[22]基于类似的理论，采用了振荡数值试验在频率域中直接获得对应的衰减和速度频散。采用孔隙力学数值模拟方法，利用固体颗粒的速度和孔隙压力等物理参数描述模型中局域流的变化。这三种方法的优越性在于，它能够将宏观尺寸模型等效成为一个中观单元体(REV)，通过研究这一中观尺度的单元体来得到宏观尺度下介质的物理参数。这种数值模拟方法主要用来评估复杂介质中的衰减和速度频散，但是对于非周期性介质中可能会产生的局域流的干扰对衰减和速度的频散影响则没有研究。然而这种干扰所造成的影响可能会很大，在某些松散岩层中，局域流扩散的尺度可能会达到10m[23]，这就会对固体颗粒的速度产生影响，进而影响最终的地震波衰减。因此模拟包含局域流之间的相互干扰作用以及其对衰减和速度的影响，将会是本文的研究重点。

本文采用有限元方法，研究一维层状孔隙介质模型中，不同局域流之间的相互干扰及其对衰减所造成的影响。首先，提出了流体相对速度的概念；其次，研究了具有不同岩层分布的周期性介质模型中，单点对应的局域流干扰情况；最后，从全局角度研究了在具有相同有效饱和度的随机孔隙模型中，不同的均方差所造成的局域流干扰对平均固体速度的影响，以及其引起的衰减和速度频散的变化。

1 流体相对速度和局域流干扰

1.1 蠕变数值模拟方法

传统意义上，Biot’s 孔隙弹性方程可以用来描述孔隙介质中的弹性波。然而在准静态(低频)的情况下，惯性耦合作用可以被忽略，此时，局域流所引起的效果可以采用Biot固结静态方程进行描述。这里采用了数值蠕变试验来获得对应的速度衰减和液体的相对速度。

Biot 固结方程如下所示

(1)

变量上的点号表明了一阶时间偏导数，而符号表示对空间的求导。P代表了孔隙压力，σ代表了固体骨架应力。 材料参数k和η分别表示了渗透率和黏度。Ks和Km分别表示了固体颗粒和骨架的体积模量。M是孔隙介质的一个独立弹性常数。

(2)

(3)

(4)

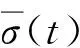
(5)

在上式的基础上，可以获得对应的P波相速度(Vp)和逆品质因子(1/Q)

(6)

(7)

式中：ρ表示的是密度，ω表示角频率，Re表示复数的实数部分。

1.2 流体相对速度

低频下，根据Darcy’s 定律，孔隙介质中的流体速度V(t)可近似表示为下式

(8)

数值模拟过程中，可以直接获得每一个时间步长所对应的流体相对速度。在此基础上，将其通过傅里叶变换转换到频率域，可以得到下式

V(w)=|FFT(V(t))|

(9)

式中：ω表示角频率(=2πf)。 文中，需要指出的是，这里所采用的是流体相对速度的绝对值。

2 数值计算结果及分析

为了能够观测到不同的局域流的干扰作用以及其影响结果，这里采用蠕变试验，分析模型内部的局域流分布情况，从而研究局域流之间的相互干扰，以及局域流的干扰所导致的纵波衰减的变化。

双相孔隙介质模型由相同的背景孔隙介质组成，所不同的是S1层中的孔隙由水填充；S2则是由气体所填充。同时，为了体现出周期性介质的对称性，这里采用了不排水边界(Undrained Boundary)作为数值模拟的边界条件，即在边界处，流体的流速为零。模型的具体参数见表1和表 2。孔隙介质中的剪切模量可以通过下式来估计计算

(10)

式中：μ表示孔隙介质骨架的剪切模量，而Kd表示的则是孔隙介质骨架的体积模量，下标1和2分别用来表示S1层和S2层固体骨架。

假设S1层和S2层中介质颗粒相同，且其颗粒直径和曲率一致。在已知S1层渗透率k1情况下，可以通过方程(11)来估计S2层中的渗透率k2

(11)

式中：k表示孔隙介质渗透率，而φ表示的则是孔隙介质的孔隙度。

模型的具体参数包括，充填水的密度是1 020kg·m-3，体积模量是2.8GPa，黏度为1.6cP；充填气体的密度是340kg·m-3，体积模量是0.29GPa，黏度为0.01cP；

孔隙介质模型中砂岩S1和S2构成参数相同，其固体颗粒的颗粒体积模量Ks为38.0GPa，颗粒密度ρs为2 650.0kg·m-3；砂岩骨架体积模量Kd为16.90GPa，剪切模量μ为13.96GPa，孔隙度φ为0.2，而渗透率k是2·10-13m2。

2.1 局域流干扰的分布特征

取图 1中任意一个周期内的介质作为特征单元体。单元体的一共包括三层，如果第一层和第三层的物理力学参数完全一样，称之为对称性周期介质；反之，如果第一层和第三层物理力学参数不同，则是非对称式周期介质。

针对对称性周期性模型，采用了图 2(a)所对应单元体来代替对称式周期性介质；而对于非对称性周期性模型，这里选择了图 2(b)来代替非对称性周期性介质。图2所示的是图1中所对应的单元体，在垂直层面的稳态纵波作用下，孔隙介质整体表现为单轴应变状态。此时，采用不排水边界。通过改变第三层S1的层厚，从而改变的孔隙压力梯度，进而诱发不同的局域流和不同的局域流之间干扰。为了研究不同局域流之间的干扰，这里选择了S2层中在0.10～0.30m区间内，均匀分布的6个点0.15、0.17、0.19、0.21、0.23和0.25m。

(a)左对称性周期介质 (b)右非对称性周期性介质图1 不同的周期性介质

(a)对称性周期性介质，(b)和(c)则是非对称性周期性介质图2 周期性介质模型

1) 局域流过渡频率。这里选择了S2层中的六个点，描述三个模型中局域流的分布特征，并且在此基础上提出了局域流过渡频率的概念。

所谓过渡频率，即考虑到频率域中流体相对速度具有高低极限(见图 3a)，在低频极限下，流体相对速度是一个恒定的值，而在高频下也对应一个恒定的值(见图 3a)，而过渡频率则是作为区分两种极限的频率界限。该频率可以通过对频域上的流体相对速度求其关于频率的一阶偏导，得到流体相对速度一阶偏导数的最大绝对值所对应的频率即过渡频率。

在稳态纵波作用下，S2层上下两个界面(见图 3)，会存在两种不同的压力梯度，这种梯度会诱发两种局域流。总体而言，这里层厚较大的S1那一层所对应的局域流，其隙压力梯度较大，称之为强势局域流，反之则称之为弱势局域流。这是因为低频下，S1层厚越大，所诱发的压力梯度也越大，造成的局域流也越强(见图3)。

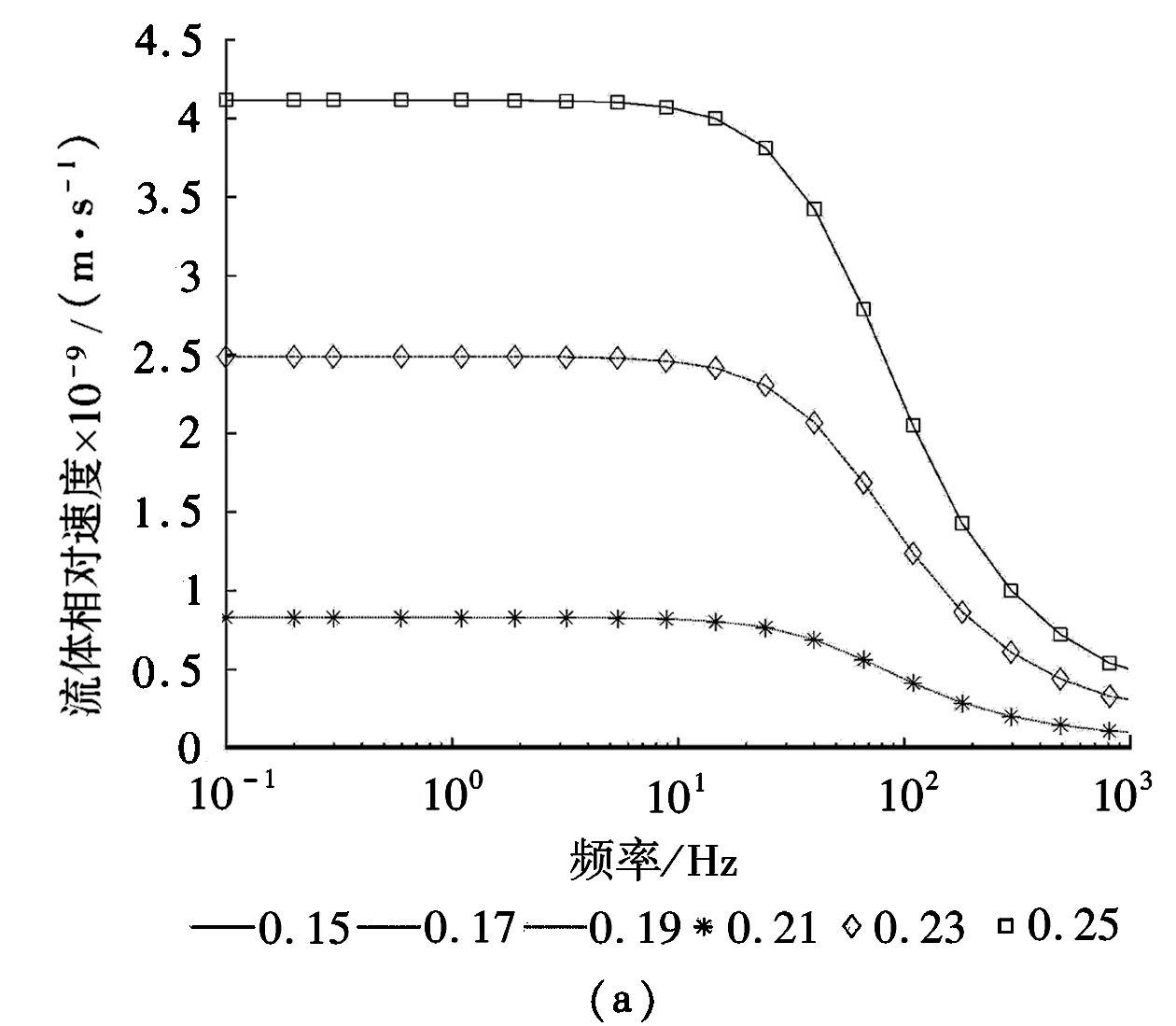
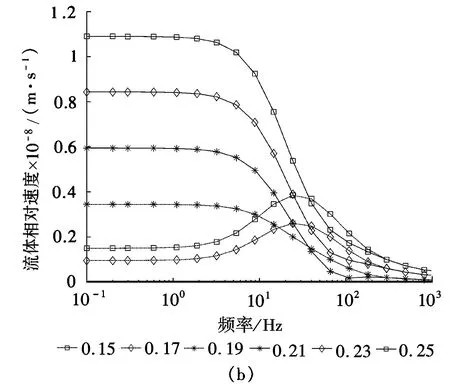
图3 频域中流体相对速度的变化曲线

为了辨识不同的局域流，这里通过设置局域流过渡频率来描述不同的局域流。图1(a)对应的是周期性对称模型，其中各点局域流的过渡频率的分布近似于一致，表明两种局域流是一致的。同时由图2(a)可知，由于模型结构的高度对称性，对称点的液相流速相互重合，这也验证了采用局域流过渡频率描述局域流分布的合理性。对于非对称结构，其内部的局域流分布也是非对称的。对于强势局域流，其变化趋势依旧保持了递减的趋势，其局域流过渡频率近似保持一致。但是对于弱势局域流，随着频率递减，已经出现了‘波峰’的现象，这种波峰现象，即是因为强势局域流对弱势局域流的干扰所造成的，图3(c)中的点0.17反应出这种‘波峰’趋势。

根据图3(b)和图3(c)可知，随着第三层层厚的增加，对应的强势局域流的过渡频率开始下降。这就表明了局域流的过渡频率跟各自层厚的长度呈反比关系。同时，强势局域流在此过程中，占据了含气层S2的大部分，即此时强弱局域流的分界点已经不在S2层的中点，而是逐渐向模型上层S1靠拢。

2) 衰减以及速度频散曲线。利用了第2节的方法对图1所示的三种模型，计算其衰减和频散曲线，周期性层状介质中的纵波衰减和速度频散如图4所示，图4图例中的‘a’，‘b’和‘c’分别代表了图 2中的三种模型。

White模型是用来描述对称性周期孔隙介质模型的(见图1(a))，为了检验蠕变试验的正确性，这里同时采用White理论和蠕变试验计算对称性周期介质的衰减曲线来验证蠕变试验的正确性。图 4(a)图例中‘White’表示利用White平面波模量计算出来的逆品质因子(1/Q)。根据图 4(a)可知，White模型的结果和蠕变试验的结果一致，这也论证了通过蠕变试验获得对应衰减值的可行性和适用性。

图4中衰减曲线和速度频率曲线表明，随着第三层的厚度的增大，衰减峰值频率(衰减峰值对应的频率)逐渐减小。衰减峰值则开始略微减小。而且随着第三层层厚的持续增大，不同局域流所引起的双峰衰减已经在图4(c)中有所体现。

以上结果表明，在周期性介质中，内部并不存在干扰，此时衰减值达到了最大，峰值频率也达到了最大，而随着第三层层厚的增大，局域流相互的干扰增强，使得衰减值逐渐变小，衰减峰值频率递减。

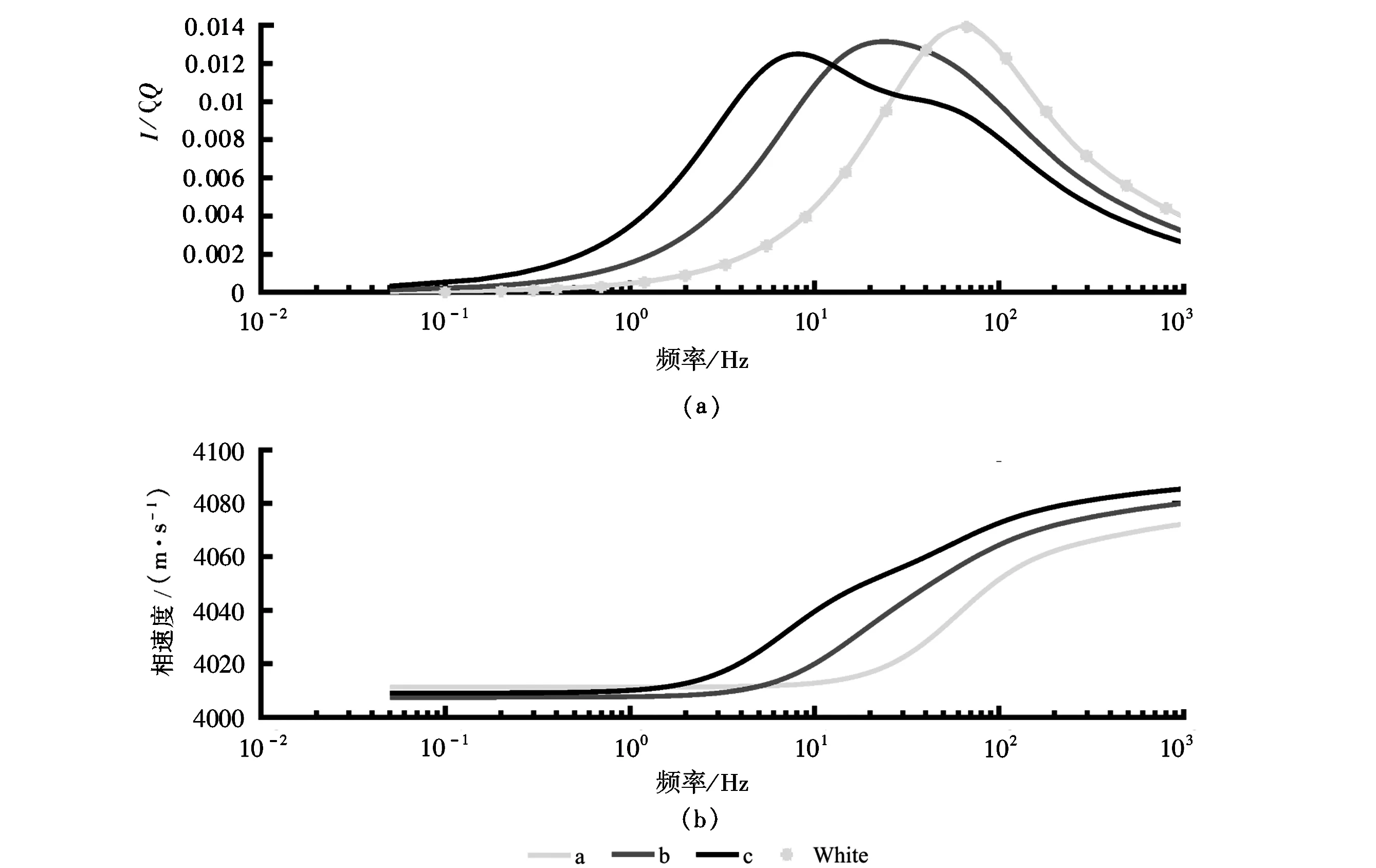
图4 衰减和速度频散变化示意图

2.2 随机层状孔隙介质中局域流干扰的影响研究

前文的分析研究了纵波在非对称单元体传播时，局域流的相互干扰，以及对应的衰减和频散。本节中将继续采用蠕变数值模拟方法，对随机层状孔隙介质中局域流之间的干扰进行数值计算研究。研究内容主要包括，在不同的含水饱和度之下，局域流干扰对随机层状孔隙模型中的平均固体颗粒速度的影响，此外还对随机层状模型中纵波频散和衰减进行分析。

随机层状孔隙介质由50对岩层(见图5)组成，每一对层中，含水层S1在其上而含气层S2则是在其下。为了减小尺寸效应所造成的影响，这里每一双层尺度均是2m，因而模型的总厚度是100m，这一大尺度可以有效避免不排水边界所带来的负面影响。为了研究含水率大小对局域流干扰的影响，可以根据平均饱和度的不同将模型划分成三大类，每类的平均含水饱和度分别是37.5%，50.0% 和62.5%；同时为了研究不同局域流干扰

强弱程度，本节对每一类饱和度中的含水层厚设置标准差为0m、0.125m、0.375m和0.625m。为了实现这一布局，这里采用了Matlab (MathWorks)中的normrand 函数。图 6显示了在不同的含水饱和度之下，对应于不同的含水层厚标准差的柱状图，图6中5代表的标准差是0.125 m、15代表了0.375 m而25则代表了0.625m。

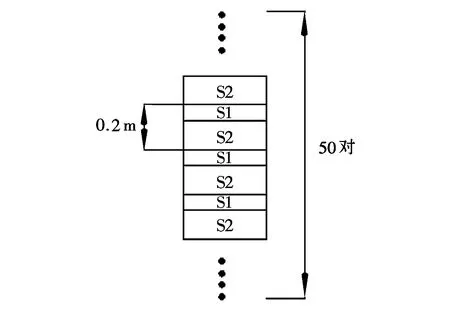
图5 随机层状介质模型

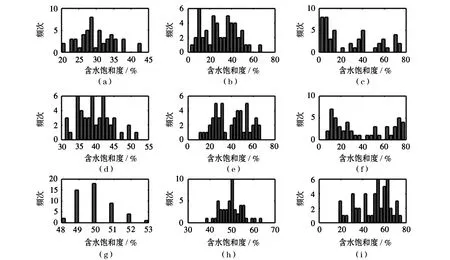
模型a、b、c平均饱和度为37.5%；d、e、f平均饱和度为50.0%；g、h、i平均饱和度为62.5%图 6 不同平均含水饱和度之下，不同的标准差所对应的含水层分布柱状图

1) 局域流干扰对固体颗粒速度的影响。由于固液之间存在的耦合作用，局域流的干扰不仅仅对液体相对速度有影响，其对模型的固体颗粒也有影响，而这种影响直接导致衰减因子的变化(见式7)，因此这里选用固体颗粒的平均速度来展现局域流干扰，以分析局域流的变化情况以及所产生的影响。

采用蠕变数值模拟试验，对图 6所示模型进行计算。综合而言，随着频率的上升，局域流干扰对固体颗粒速度的扰动程度呈现逐渐降低的趋势；而随着综合平均含水饱和度的增大，局域流干扰对固体颗粒的速度的影响加大，这种加大的趋势在低频下表现得更为明显，尤其是在高饱和情况下(图 7c)。同时，在相同的模型结构情况下，对于低饱和度而言(图 7a)，干扰作用主要体现在[0.2～10]Hz频段之间，而对于高饱和度而言(图 7a和c)，干扰发生的频段开始向更低频段(<5Hz)移动。

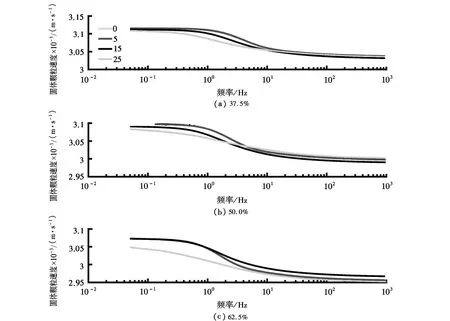
图7 不同平均含水饱和度下固体颗粒速度随频率的变化

2) 衰减以及速度频散曲线。以下将研究局域流的相互干扰对地震衰减和速度频散所造成的影响。如图8所示，对同一饱和度而言，标准差越大，其对应的干扰作用也就越大，所导致的衰减峰值也越来越小，尤其是高饱和度之下，这种趋势表现得更为明显(见图8c)。对应的衰减峰值频率也在逐步减小。这一特征在图 8a、b和c中均有所体现。而随着饱和度的增大，干扰对衰减的影响也在加大，衰减的下降幅度明显加剧。

通过对比各个频率之下纵波相速度可知，在高频之下，各个饱和度对应的高频纵波速度保持一致；而在低频下，低饱和度对应的相速度的频散程度最小，而高饱和度对应的相速度的频散程度最大。这是因为当地震波在孔隙介质中传播地震波的频率足够高的时候，此时的地震波长远远小于孔隙介质的非均匀尺度，孔隙介质中不同流体压力下的流相来不及发生相对流动，故此时整个孔隙介质整体呈现出弹性的状态。所以在高频下，当随机孔隙介质中各种平均物理参数一致的情况下(见表1～表 2)，随机介质中的纵波速度趋于一致。而在低频之下，此时的地震波长与孔隙介质的非均匀尺度处于同一数量等级，此时局域流的干扰作用开始增大，导致纵波相速度的频散程度加大。该结论与图 7中的结果保持一致，即干扰作用主要发生在低频段，而高频之下，干扰作用几乎可以忽略不计。

图8 不同饱和度下的衰减和速度频散曲线，图标中的数字代表了含水层厚度的标准差

3 结论

对于对称性结构而言，蠕变数值试验的结果和White模型的结果差异很小，可以认为蠕变试验可以很好地模拟复杂介质条件之下，中观尺度局域流所造成的衰减以及对应的速度频散。

(1) 对于非对称性结构而言，局域流干扰是一个动态的过程。

对称性周期性孔隙层状介质中，每个单元体中所包含的局域流强度相同，因而彼此之间并没有液液耦合的扰动。而对于非对称性周期性介质而言，内部的局域流不尽相同，相互之间存在着扰动，导致了介质内部不再存在流体静止的点，即其内部存在一直存在不同局域流的相互扰动。这也意味着如果直接采用Undrained边界条件剖分不同的局域流会带来一定的误差。

(2) 在全局尺度上，局域流的相互干扰作用不仅仅跟含水层厚标准差有关，也跟饱和度有关。

当含水层层厚标准方差变大，即对应上下含水层层厚差异性更为明显，这就意味着不同局域流之间的扰动也越来越大。而随着扰动强度的增大，对其中的固体颗粒的速度产生很大的影响。同时随着综合平均含水饱和度的增大，局域流干扰强度随之增大，这对固体颗粒的速度的影响有所增强。

(3) 局域流干扰的作用主要发生在f<100Hz的频段之下(见图3和图7)。而在其他高频段下，干扰的作用逐渐变小，中观局域流趋于稳定。因此在局域流干扰对高频极限下纵波模量影响不大。

在高频范围内，局域流干扰对固体颗粒速度的扰动程度呈现逐渐降低的趋势，这是因为随着频率的增大，流体耗散时间减小，这使得局域流的影响范围缩小，因此局域流扰动的效果急剧减弱，因而在高频范围内，具有不同含水层厚度方差的模型中，衰减(1/Q)趋向于一致；而在低频范围内，流体耗散时间偏大，这使得局域流得影响范围偏大，因而局域流扰动的效果增大，因此在低频范围内，衰减(1/Q)差异显著。

考虑到实际情况下，孔隙性岩层中往往包含了多重局域流，不同局域流之间容易产生相互干扰。而经典White模型，仅仅适用于周期性对称介质，该介质中并不包含多重局域流之间的干扰。因此，针对局域流相互影响的研究可以用来修正经典的White模型，使之能够更好的描述由于局域流干扰所引起的衰减变化。