平口管口处气泡行为特征数值模拟

2019-01-21，，，，

长江科学院院报 2019年1期

，，，，

(内蒙古科技大学能源与环境学院，内蒙古包头 014010)

1 研究背景

气液两相流广泛存在于石油化工、能源应用、水利工程、环境工程等工业领域。对于气液两相流流动，气泡的形成及运动过程尤为重要。如污水处理和江河水质净化系统中的溶气气浮机、曝气机等设备，就是利用气泡特性来去除池内杂质，提高水质的清洁度；鼓泡床和旋流分离器等设备中，气泡运动过程中的流体力学特性对设备运行至关重要。

为此，国内外许多学者用各种方法，针对气泡在液体中的上升过程及其影响因素进行了广泛研究[1-4]。根据气泡管口的浸没方式不同，可分为管口向上的底部浸没(底吹)、管口水平布置的侧面浸没(侧吹)和管口向下的顶部浸没(顶吹)3种浸没方式[5]。其中，管口向上的底部浸没应用最为广泛，且研究较多。Qu等[6]通过试验方法，研究了微孔下气泡运动行为，发现在低Bond数下，随着韦伯数的增加，气泡从单气泡上升阶段慢慢变为多泡聚并阶段。Bari等[7]通过试验方法，研究了气泡膨胀和脱离过程中单个气泡周围力场和气泡生成及脱离过程中气泡形状和压力场的相互依存关系。徐玲君等[8]采用VOF模型对直径为2.6 mm和4 mm的气泡进行数值模拟，得到单个气泡在静水中的上升路径和上升速度等。Premlata等[9]利用VOF模型，得到不同Ga数和Eo数对气泡长宽比、重心位置的影响规律。Georgoulas等[10]则采用VOF模型，模拟了3维轴对称模型下气泡膨胀脱离过程，研究发现气泡脱离特性受表面张力，液相密度和重力的影响较大，而受液相动力黏度的影响较小。Huda等[11]基于双欧拉方法研究了侧吹时管口浸没深度以及气流量对液池溶液运动的影响。王冲等[12]通过试验的方法，研究了顶吹时气液两相流动，并发现顶吹能产生一定深度的气泡群，其搅拌深度随气量的增大而增大。

上述研究仅局限于3种管口浸没方式中的一种，少有针对3种管口浸没方式下气泡特性的对比研究；且以往研究主要关注气泡的上升运动过程，而对气泡在不同浸没管口处膨胀脱离特性研究较少。而气泡在管口处的膨胀脱离特性对气泡后期的上升运动有较大影响。本文作者[13]前期对气化炉液池内气液两相流进行了数值模拟研究，获得顶部浸没方式下气泡流动特性。在此基础上，本文采用数值模拟方法，对3种不同管口浸没方式下单个气泡的膨胀、脱离特性进行综合对比研究。

2 模拟理论与方法

2.1 控制方程

首先作以下假设：①两相流动在等温绝热条件下进行；②气液两相均为不可压缩的牛顿流体；③界面所分隔的两相流体系为单相流系。质量守恒方程与动量守恒方程分别为：

(1)

ρgi+FV。

(2)

式中：ρ为流体密度；xi,xj为i和j方向上的运动距离；ui,uj为i和j方向上的速度矢量；p为压强；μ为动力黏度；g为重力加速度；FV为体积力。

VOF模型中，不同的流体共用一套控制方程，通过引入相体积分数这一函数α实现对相界面的追踪。体积分数方程表示为

(3)

控制方程的密度和黏度，由每一相体积分数决定，即求混合平均参数：

ρ=αfρf+(1-αf)ρg；

(4)

μ=αfμf+(1-αf)μg。

(5)

式中：下角标f表示液相；下角标g表示气相。

对于气液交界面上的表面张力，采用Brackbill等[14]提出的连续表面张力模型，这个模型把表面张力转化为控制容积的体积力，即：

(6)

(7)

n=α。

(8)

式中：σ为表面张力系数；n为表面法向量；k为表面曲率。

2.2 计算条件及网格划分

模拟在非稳态条件下基于VOF两相流模型进行。采用PISO算法实现压力与速度耦合，无滑移壁面，速度进口，压力出口，此模型为开放系统，设定压力出口的压力值为标准大气压。模拟中所用气体为理想状态下的空气，液体为水，初始条件及气液两相物性参数见表1。

表1 气液两相的物性参数Table 1 Physical properties of gas-liquid two-phase

图1 网格无关性验证Fig.1 Grid independence verification

首先进行网格无关性验证，从而确定合适的网格尺寸。如图1所示，当气体速度为0.1 m/s时，网格尺寸为0.3 mm×0.3 mm，相对于0.1 mm×0.1 mm的网格，气泡膨胀脱离时间的相对误差为3.17%；当气体速度为0.2 m/s时，两者气泡膨胀脱离时间的相对误差为3.12%。可见，当网格尺寸为0.3 mm×0.3 mm时，既能保证网格无关性的要求，又能节约计算时间。

3 模型验证

将模拟结果与本文作者前期完成的试验结果[15]进行对比分析。图2和图3分别为试验和模拟条件下获得的顶吹方式下气泡膨胀脱离过程。气泡从最初的球帽状最终演变成椭球状，同时，模拟和试验获得的气泡演变形状基本吻合。另外从图4可知，模拟条件下气泡脱离直径比试验条件下气泡脱离直径大。其原因是试验条件下气体速度不容易控制，采用的是平均气体速度；模拟是在理想条件下进行,与试验难免有些区别，但试验结果与模拟结果总体趋势较一致，即随着气体速度增大，气泡直径也增大。通过与试验结果对比，验证了本文所建模型的正确合理性。

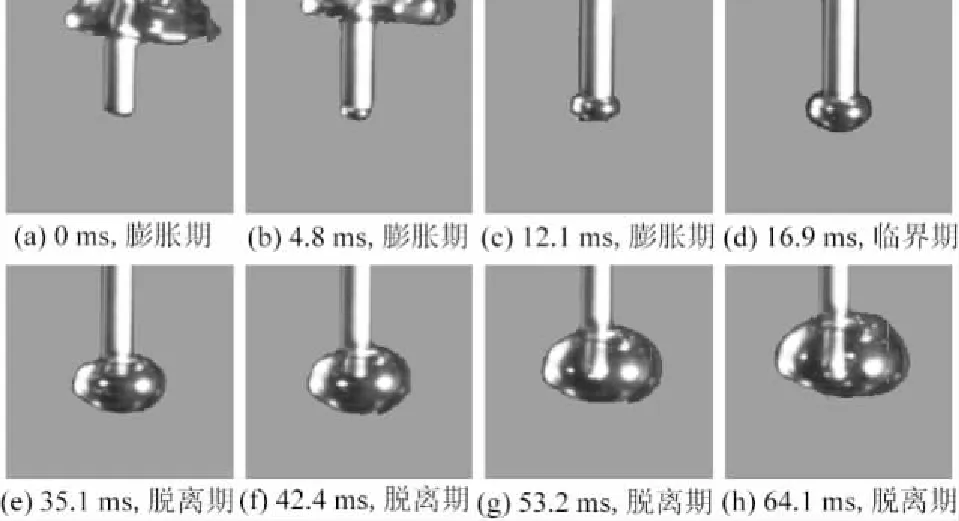
图2 顶吹时气泡膨胀脱离过程试验结果Fig.2 Experimental results of bubble expansion and detachment process in top-immersion mode

图3 顶吹时气泡膨胀脱离过程模拟结果Fig.3 Simulation results of bubble expansion and detachment process in top-immersion mode

图4 气泡脱离直径随气体速度的变化规律Fig.4 Change of bubble detachment diameter with gas velocity

4 结果与分析

4.1 3种管口浸没方式下气泡膨胀、脱离演变过程

图5为底吹时气泡膨胀脱离运动过程。图5(a)—图5 (c)为气泡的膨胀期，气泡首先在出口处生成，然后气泡底部向管口两侧扩张，气泡的高度增高。在56 ms时刻(图5(d))，气泡底部不再向管口两侧移动，气泡底部产生收缩的趋势，该时刻定义为气泡膨胀脱离的临界期。图5(e)—图5 (h)为气泡脱离期，气泡继续向上发展，底部逐渐缩小从而在管口上部形成一个细长的颈部，最后在管口上方一定高度脱离管口。气泡膨胀脱离过程主要受气泡内外的压差决定，当气泡的内侧压力大于气泡外侧压力，气泡表现为膨胀过程；气泡处于缩颈阶段时，气泡所受浮力起到主导作用，促使气泡向上脱离。

图5 底吹时气泡膨胀脱离过程Fig.5 Bubble expansion and detachment process in bottom-immersion mode

顶吹时气泡的膨胀脱离运动过程由图3给出。图3(a)—图3(c)为气泡膨胀期，气泡主要向管口下方膨胀，气泡由球帽状演变到半球状。在32 ms时刻(图3(d))，气泡表现出向上脱离趋势，此时定义为气泡膨胀脱离的临界期。图3(e)—图3 (h)为气泡脱离期，气泡体积在该阶段继续膨胀，此时气泡所受浮力起到主导作用，从而使气泡开始做向上脱离运动。

图6为侧吹时气泡膨胀脱离运动过程。图6(a)— 图6 (c)为气泡膨胀期，气泡的膨胀方向主要为管口正前方。伴随着气泡体积的增大，气泡所受浮力影响也变大，气泡膨胀表现为与管口呈一定角度的运动形态。在48 ms时刻(图6(d))，气泡有向上脱离的趋势，该时刻定义为气泡膨胀脱离的临界期。图6(e)— 图6 (h)为气泡脱离期，气泡的体积继续变大，同时气泡开始出现颈缩现象，其用时约52 ms，占整个膨胀脱离时间的48.1%。由于管口布置在侧面，气泡膨胀的方向与气泡所受浮力、质量力、曳力等不在同一条直线上，导致气泡脱离形状呈现不规则性。

图6 侧吹时气泡膨胀脱离过程Fig.6 Bubble expansion and detachment process in side-immersion mode

4.2 管口气体速度对气泡行为特性的影响

图7(a)为底吹时不同管口直径下气泡膨胀脱离时间随管口气体速度的变化规律。在相同管口气体速度下，对于气体速度<0.2 m/s时，除管口直径为2 mm的气泡膨胀脱离时间较长外，其它3种管径气泡膨胀脱离时间几乎一致。究其原因，当气流速度较小时，气泡脱离主要受到浮力的影响，而浮力大小主要取决于气泡的体积。图7(b)为底吹时不同管径下气泡脱离直径随管口气体速度的变化规律。由图7(b)可知，当管径为2 mm时形成气泡的直径最小，从而导致该管径下的气泡膨胀脱离时间最长。在同一管径条件下，气泡膨胀脱离时间随管口气体速度的增大而变小。气体速度为0.2 m/s是一个转折点，当气体速度<0.2 m/s时，伴随气体速度的增大，气泡膨胀脱离时间明显降低；而气体速度>0.2 m/s后，随气体速度的增大，气泡膨胀脱离时间没有明显变化。由此可见，通过增加气体速度来缩短气泡膨胀脱离时间必然存在一个最佳气体速度。

图7 不同管径下的管口气体速度对气泡行为特性的影响Fig.7 Effect of gas velocity on bubble behavior in the presence of different pipe diameters

由图7(b)可知，当气体速度相同时，气泡脱离直径随管口直径的增加而增大。在低气体速度时，虽然2 mm直径管口的气泡膨胀脱离时间较长，但从图7(b)明显看出，管口直径对气泡脱离直径起主导作用，在高气体速度时表现得更为明显。当管径相同时，气泡脱离直径随气体速度的增加而增大，从气泡脱离直径的增长趋势来看，很显然管口直径为6 mm时，气泡脱离直径增加的斜率最大，其余3种管径气泡脱离直径随气体速度增加变化斜率相近。

图8(a)为3种管口浸没方式下气泡膨胀脱离时间随管口气体速度的变化规律。3种管口浸没方式下，气泡的膨胀脱离时间随气体速度的增大而缩短。通过增加气体速度的方式来缩短气泡的膨胀脱离时间存在一个最佳速度，对于底吹与顶吹2种方式其最佳脱离速度为0.2 m/s；而侧吹方式下最佳脱离速度应<0.2 m/s。针对同一气体速度，底吹方式下气泡膨胀脱离时间最短，侧吹方式下气泡膨胀脱离时间最长。底吹比顶吹气泡的膨胀脱离时间短，这是因为，气泡在膨胀阶段，气泡所受浮力对气泡膨胀起到促进作用；气泡进入到脱离阶段时，底吹方式下，气流的流向有助于气泡的脱离，而顶吹方式下，气流的流向不利于气泡脱离的进行。侧吹方式下，管口气流方向与气泡在液体中所受的浮力、质量力、曳力等不在同一条直线上，与前2种管口浸没方式相比，气泡膨胀脱离路径要复杂，以及气泡脱离期时气泡缩颈所用时间较长，并且形状的不规则都延长了气泡膨胀脱离时间。

图8(b)为3种管口浸没方式下气泡脱离直径随管口气体速度的变化规律。3种管口浸没方式下，气泡脱离直径随气体速度的增加而增大。顶吹时得到的气泡脱离直径，要比底吹方式下气泡脱离直径大，这是由于相同气体速度条件下，顶吹时气泡膨胀脱离时间比底吹时气泡膨胀脱离时间长。侧吹方式在低气体速度条件下，气泡的脱离时间最长而气泡的脱离直径较小。其中主要原因是侧吹方式下，气泡进入到脱离期后，有一段较长的缩颈过程，缩颈的存在阻碍了气泡体积的变大，导致气泡直径较小。在低气体速度时，3种管口浸没方式下，气泡直径差距不大。

图8 3种浸没方式下管口气体速度对气泡行为特性的影响Fig.8 Effect of gas velocity on bubble behavior in three immersion modes

4.3 表面张力对气泡行为特性的影响

图9(a)为3种管口浸没方式下气泡膨胀脱离时间随表面张力的变化规律。底吹与顶吹2种浸没方式下，随着表面张力的增大，气泡膨胀脱离时间也变长。从图9(a)中的斜率来看，底吹方式气泡膨胀脱离时间较顶吹方式更容易受到表面张力的影响。表面张力增加会阻碍气泡的生成及上升运动，表面张力的增大在一定程度上增加了气泡的膨胀脱离时间。对于侧吹方式，气泡膨胀方向与气泡受力方向不在同一直线上，气泡膨胀脱离时间随液体表面张力的增加，呈现的规律不明显但也有上升趋势。

图9(b)为3种管口浸没方式下气泡脱离直径随表面张力的变化规律。同一液体表面张力时，顶吹方式下气泡脱离直径要比底吹所得到的气泡脱离直径大；两者气泡脱离直径的差距随表面张力的增大而缩短。对于侧吹方式下，气泡膨胀脱离时间最长而气泡脱离直径反而最小，主要原因为侧吹方式下虽然气泡的膨胀脱离时间最长，但气泡进入脱离期之后，缩颈阶段所占总时间的比重较大，影响了气泡膨胀的有效进行。底吹和顶吹2种方式下，气泡脱离直径随液体表面张力的增大而明显增大。

图9 3种浸没方式下表面张力对气泡行为特性的影响Fig.9 Effect of surface tension on bubble behavior in three immersion modes

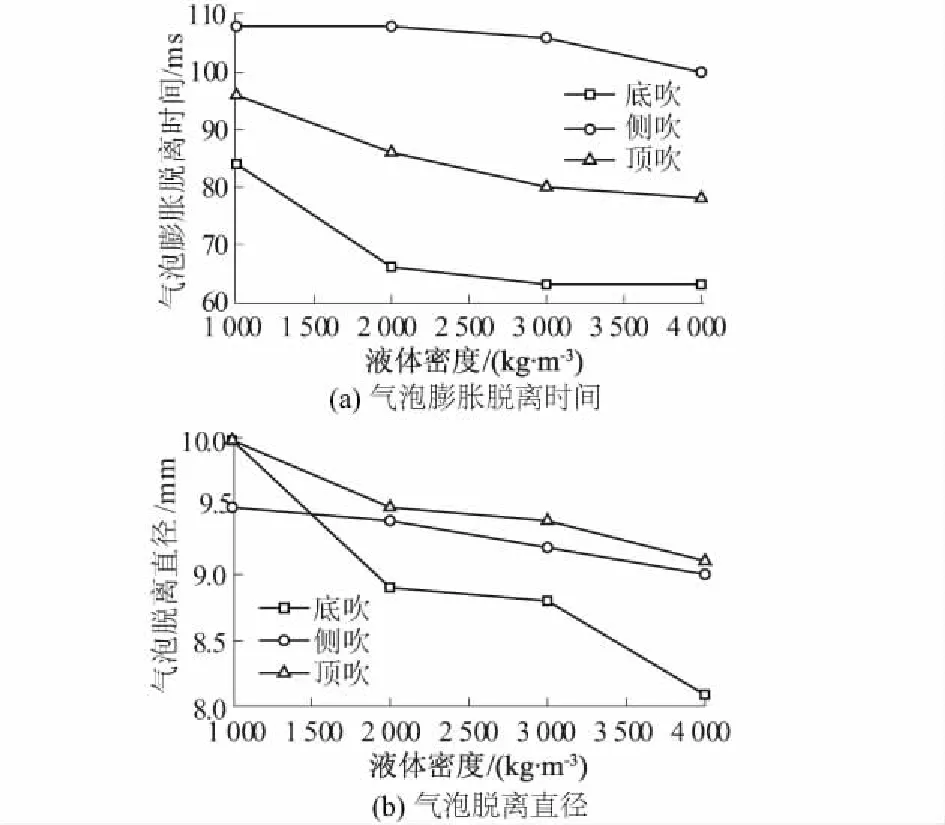
图10 3种浸没方式下液体密度对气泡行为特性的影响Fig.10 Effect of liquid density on bubble behavior in three immersion modes

4.4 液体密度对气泡行为特性的影响

图10(a)为3种管口浸没方式下气泡膨胀脱离时间随液体密度的变化规律。3种管口浸没方式下，气泡膨胀脱离时间随液体密度的增大而降低。底吹和顶吹方式下，液体密度从1 000 kg/m3增加到2 000 kg/m3，气泡膨胀脱离时间分别降低了18 ms和10 ms，而之后随液体密度的增加，气泡膨胀脱离时间变化不大。在相同液体密度条件时，侧吹方式下气泡膨胀脱离时间最长；底吹方式下气泡膨胀脱离时间最短。

图10(b)为3种管口浸没方式下气泡脱离直径随液体密度变化的规律。由图10(b)可知，气泡的脱离直径随液体密度的增大而减小，其中底吹方式时表现得最为明显，侧吹方式下气泡脱离直径受液体密度的影响最小。侧吹和顶吹方式下，顶吹比侧吹时气泡脱离直径略大，其主要原因是侧吹时脱离期的缩颈过程阻碍了气泡体积的有效膨胀。