连续微弯弯道水力特性试验及模拟研究

，

(1.长江科学院 流域水环境研究所，武汉 430010； 2.长江科学院 流域水资源与生态环境科学湖北省重点实验室，武汉 430010； 3.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072)

1 研究背景

弯曲型河道是组成河流的基本单元之一。陈启刚等[1]利用PIV系统研究了弯道水流三维平均流和平均运动规律。De Vriend[2]求解完全的N-S方程，模拟了微弯浅水、充分发展的层流流动。李义天和谢鉴衡[3]研究了冲积平原河道平面二维流速分布。董耀华[4]建立了极坐标下的弯道水流平面二维数学模型，并指出弯道水流数学模拟的关键在于弯道水面形态和流速重分布的模拟。杨燕华等[5]基于雷诺方程和有限体积法建立连续弯道水流的三维数学模型，研究了弯道水流纵向流速剖面的变化。Stoesser等[6]采用不同方法模拟弯道水流结构，比较分析了不同模拟方法下的流速和壁面切应力分布规律。陈翠霞[7]采用标准的κ-ε模型和RMGκ-ε模型，实现了κ-ε模型和Reynolds 应力模型等4种紊流模型对连续弯道的模拟计算，结果显示，Reynolds 应力模型的计算值最接近实测值。

弯曲型河道中曲折系数是影响水力特性的重要参数，天然河道的曲折系数通常较小。小曲折系数弯道介于顺直河道和弯曲河道之间，这决定了其水流结构与大曲折系数弯道存在较大差异[8]。以往大多数学者都将重点放在较大曲折系数的弯道水流研究中，以小曲折系数弯道为研究对象的成果相对较少。本文采用小曲折系数连续弯道的概化模型进行试验，并利用Reynolds应力模型，对该模型进行模拟计算，从水面线、流速场、弯道环流及强度等方面研究了连续微弯弯道水力特性。

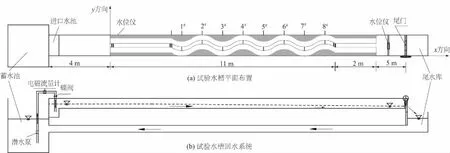
图1 试验水槽布置Fig.1 Layout of the test flume

2 试验条件及方法

2.1 试验条件

本试验模型采用概化弯道模型，平面布置如图1所示。整个试验的水循环系统由水库、水泵、蝶阀、试验水槽、尾门、尾水库、回水水槽等组成。水槽全长22 m，其中试验段长13 m，宽1 m。试验段分为进口直线段(0～3 m)、弯道段(3～11 m)和出口直线段(11～13 m)。弯道段由4个完整周期弯道组成，每个周期弯道由2段等尺度圆弧形弯段反向连接而成。弯道中心线半径为0.86 m，曲折系数K为1.07，弯道底纵坡降为0.5‰。模型断面为梯形，底宽0.20 m、高0.12 m、边坡比1∶2，床面无横比降。

2.2 试验方法

试验流量为12 L/s，水深约12 cm，断面平均流速约0.23 m/s，试验工况见表1。水槽边壁沿水流方向(x方向)从3 m开始，垂直于流向间隔0.5 m布置流速测量断面，全程共布设15个流速测量断面，见图1。采用日本JFE公司研制的ACM2-RS型二维电磁流速计测量流速，测量精度为±0.5 cm/s，频率为20 Hz。沿垂向(z方向)每隔1 cm取1个测点，沿河宽方向(y方向，正方向为由右岸指向左岸)间隔4 cm取1个测点。为尽量减少误差，每个测点至少记录600个瞬时流速，测量时间内至少经过一个紊流周期，求其平均值得到各测点的时均纵向、横向流速。共布置1 560个测点，测点布设密度适中，能较好地反映水流结构。

表1 试验工况参数Table 1 Test parameters

3 三维水流数值模拟方法

3.1 基本方程

(1)

式中：ρ为密度；t为时间；u，v，w分别为速度矢量在x，y，z方向上的分量。

动量守恒的运动方程，又称N-S方程，部分方程见式(2)。

式中:μ为动力黏度；p为流体微元体上的压力；Su为动量方程的广义源项。

根据紊流性质，速度和压强等物理量可分解为平均量和脉动量之和，见式(3)。

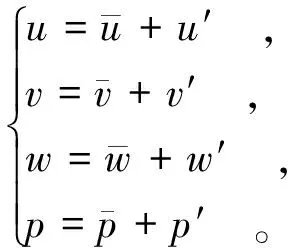
(3)

式中：上标“-”代表对时间的平均量；“′”代表脉动量。将式(3)代入式(1)和式(2)中，得到紊流时均流动的控制方程，即：

(4)

(5)

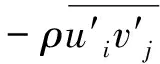
3.2 方程的离散及离散方程的解法

目前常用的离散格式有中心差分格式、混合格式、迎风差分格式、乘方格式、指数格式、QUICK格式及修正QUICK格式。本文计算模拟采用有限体积法中的迎风差分格式，该格式稳定性好，空间差分形式可依据流速的方向分为向前差分或向后差分。

二次蒸汽回收阶段，需要控制系统的蒸汽回收流速，满足蒸煮生产工艺温度。在使用中，为避免人为因素影响，该回收二次蒸汽热能系统采用微机控制，通过PLC、工业计算机（FA）、组态等形式来控制系统温度、压力、电机转速，保持系统持续平衡，发挥节能效益。

目前应用最广泛的有SIMPLE算法及在此基础上改进而建立的SIMPLER，SIMPLEC，PISO算法。本文采用PISO算法进行研究求解。

3.3 连续微弯弯道模型构建

3.3.1 模型概况

计算模型长21 m，其中进口段8 m，连续弯道段8 m，出口段5 m，与实际模型相比，计算模型进口段较长，以便水流平顺进弯。具体计算条件如表2。

表2 数值模拟计算条件Table 2 Parameters for numerical model

注：L为模型长度；Q为进口流量；H为模型高度；Ho为出口水位；Re为雷诺数；B/h为宽深比

3.3.2 网格划分

本文采用六面体结构化网格，并对水面处网格和弯段处进行加密处理。

连续弯道纵向长度为21 m，模型的横断面底宽为0.2 m，顶宽为1.0 m，高为0.2 m，进口水位13.5 cm，出口水位10.5 cm，横断面划分为25×25个网格，模型网格总数约19万个，网格划分如图2所示。

4 试验及模拟结果分析

4.1 水面线分析

4.1.1 水面纵比降分析

图3 弯道水流沿程水面线Fig.3 Water surface lines of the bend flow

以弯道进口断面为起点，绘制计算得到弯道水流沿程水面线(沿程水面线取各横向断面槽中水位值，跟试验测量位置一致)，并与实测沿程水面线比较，见图3。结果表明，采用Reynolds应力模型计算得到的水面纵比降与实测值吻合得较好，水面线沿程均匀降低。

4.1.2 水面横比降分析

水面横比降是弯道水流的重要特征。在同一弯顶断面，凹岸槽底压强大于凸岸，槽底压强由凹岸到凸岸逐步减小，表明凹岸水位高于凸岸并沿横向逐渐降低，如图4所示。

为进一步分析连续微弯弯道水面横比降，选取3#-7#弯顶断面的横向水面线进行比较。同一弯顶断面，凹岸水位高于凸岸，弯顶断面横比降均值约0.63%，如图5。

图5 弯顶断面横向水面线Fig.5 Transverse water lines in bend section

4.2 水流流速分析

4.2.1 横断面纵向流速云图分析

不同弯顶断面纵向流速分布的趋势大致相同，间隔一个弯顶断面的流速分布云图呈现一定的相似性，如图6所示。沿水流方向，靠近凸岸的纵向流速较大，且表面附近纵向流速相对较大，底部附近流速相对较小，靠近凸岸的纵向流速沿垂线随相对水深增大流速增大；而靠近凹岸一侧的纵向流速，随相对水深增大，先增大后减小。

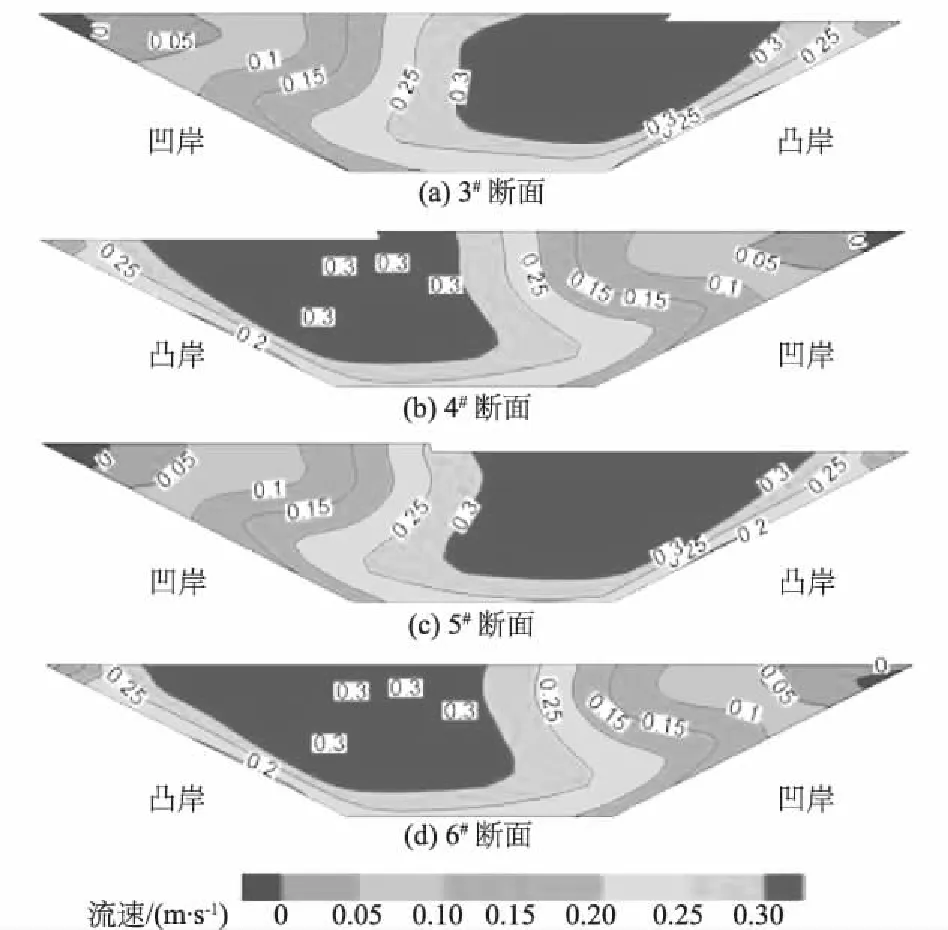
图6 弯顶断面纵向流速云图Fig.6 Longitudinal velocity field in bend section

4.2.2 弯道表层流速分析

实测的弯道表层流速矢量图和计算得到的表层流速分布规律基本一致，如图7所示。弯顶断面高流速区居水槽中间，且靠近凸岸侧，而低流速区靠近凹岸侧。

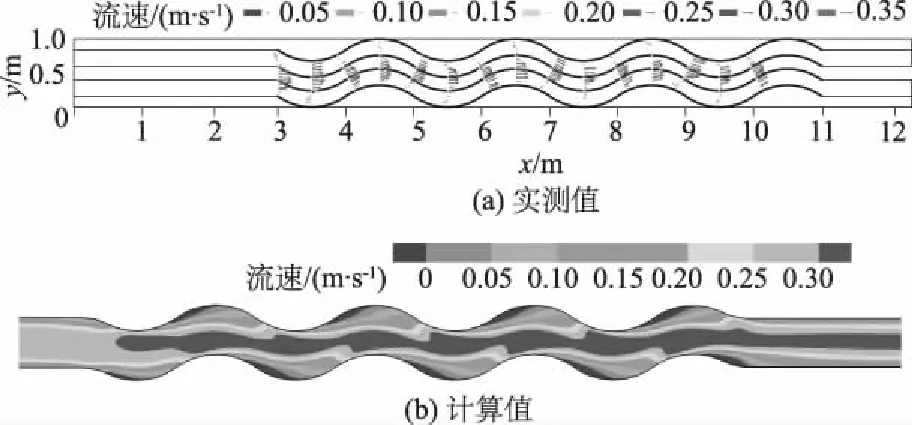
图7 表层纵向流速Fig.7 Longitudinal velocity field in surface

4.2.3 纵向流速沿垂线分布

纵向流速垂线分布选取河槽中的垂线进行分析，该位置水深较大，测点数据较多，具有代表性。选取3个典型断面分析纵向流速沿垂线分布的规律，断面测量间距4 cm，一个断面测量了6条垂线流速。

纵向流速垂线分布的实测值与计算值拟合地较好，如图8所示。弯顶断面靠近凸岸的纵向流速垂线分布接近对数流速分布，流速呈现随水深依次增大的趋势；而靠近凹岸的纵向流速垂线分布完全偏离对数流速分布，呈现随水深先增大后减小的趋势，最大流速点位于z/h(相对水深)=0.25～0.30附近，整体呈现“凸肚”形。童思陈等[9]通过对90°矩形断面单弯道进行数值模拟也发现，沿弯道凸岸，在弯道进口断面纵向流速剖面与指数公式计算值已有较大差异，弯顶之后这种差别越来越大，到出口断面更为明显，纵向流速沿垂线分布呈现“凸肚”形。

图8 纵向流速沿垂线分布Fig.8 Vertical distribution of longitudinal velocity

4.3 弯道环流分析

4.3.1 环流结构分析

小曲率弯道的环流结构跟常规弯道环流有较大差异，如图9所示。各弯顶断面呈现双环流结构形式，靠近凹岸的环流中心居上方，而靠近凸岸的环流中心居下方，靠近凹岸的环流相对完整，流速大小相比凸岸的较大。整体而言，水流表面流速从凸岸流向凹岸，这种趋势与弯曲度较大时的表层水流由凸岸流向凹岸、底层水流由凹岸流向凸岸的环流结构相对应。

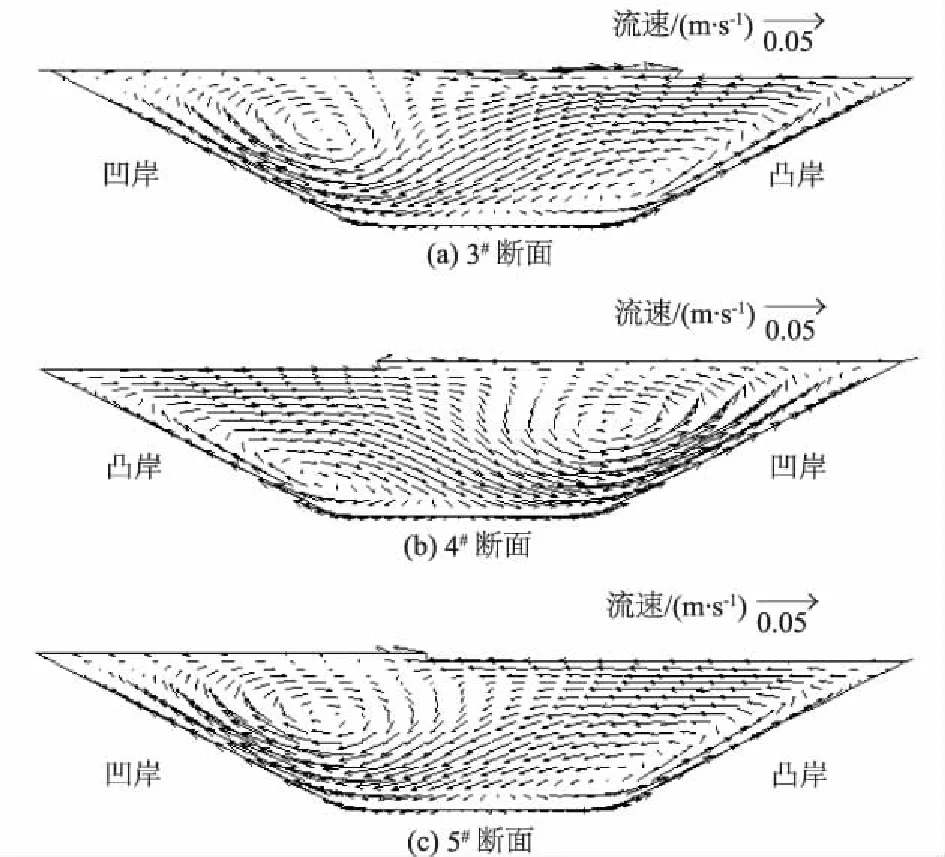
图9 弯顶断面环流结构Fig.9 Circulating flow field in bend section

4.3.2 环流强度分析

环流强度与纵向流速、弯曲程度及水深等因素有关，一般而言，在水面和河底处较大而在水深中部较小。为分析连续弯道环流强度垂线分布变化特性，选取环流旋度来表示环流强度，它关系到泥沙运动行进方向及河床局部变形的部位。

各弯顶断面环流旋度大小不同，但基本上<0.2，说明纵向流速远大于环流流速。从整体看，水面和槽底处的环流强度大于水体中部，从凹凸岸来看，凹岸的环流强度大于凸岸的环流强度，如图10所示。

5 结 论

通过建立梯形断面、小曲折系数(曲折系数1.07)的概化模型试验，并运用Reynolds应力模型进行模拟计算，研究了连续微弯弯道水力特性，主要结论如下：

(1)采用Reynolds应力模型计算得到的水面纵比降与实测值符合较好，能够较好地反映出弯道水面凹岸高凸岸低的规律，弯顶断面横比降均值约0.63%。

(2)同一断面，近凸岸的纵向流速垂线分布接近对数流速分布；而靠近凹岸的纵向流速垂线分布完全偏离对数流速分布，呈现随水深先增大后减小的趋势，最大流速位于z/h=0.25～0.30附近，整体呈现“凸肚”形。

(3)弯道环流方面，弯顶断面呈现双环流结构，靠近凹岸一侧的环流中心居上方，而靠近凸岸一侧的环流中心居下方，靠近凹岸侧的环流发展相对完整，流速大小相比凸岸较大；各弯顶均有由凸岸上方指向凹岸下方的斜向流速场。弯顶断面水面和槽底处的环流强度大于水体中部，凹岸的环流强度大于凸岸的环流强度，且基本上都<0.2。