“正方形的性质和判定”课堂实录

李 想

（江苏省徐州市第十三中学，江苏 徐州）

苏教版八年级第九章“中心对称图形——平行四边形”中主要对平行四边形、矩形、菱形、正方形的性质和判定进行了探索研究，平行四边形的性质和判定的知识探索过程直接指导了矩形和菱形的学习.我们知道，矩形和菱形的学习，主要是在平行四边形的基础之上，加入矩形和菱形的特性的学习.

【学习目标】

1．理解并掌握正方形的概念；

2．理解并掌握正方形的性质与判定，并会运用解决简单的问题；

3．了解并掌握矩形、菱形、正方形的性质与判定的区别与联系．

一、正方形概念

1．正方形定义：有_____且_____的_____是正方形．

2．正方形是轴对称图形，有_____对称轴；正方形是中心对称图形，对称中心是_____.正方形面积公式：_____或_____.

二、正方形的性质

正方形是特殊的___，而且是_____的矩形，也是_____的菱形．

∵四边形ABCD为正方形

___________；___________；

___________；___________；

_________________________；

三、四边形性质汇总

1.平行四边形：对边平行、对边相等、对角相等，对角线互相平分；

2.矩形：对边平行、对边相等、对角相等，对角线互相平分，四个内角为直角，对角线相等；

3.菱形：对边平行、对边相等、对角相等，对角线互相平分，四条边相等，对角线垂直；

4.正方形：对边平行、对边相等、对角相等，对角线互相平分，四个内角为直角，对角线相等，四条边相等，对角线垂直.

由此可见，正方形的性质包含了平行四边形、菱形、矩形的一切性质.

四、判定正方形

1．利用正方形的定义证明：______________________.关键词：________+_________+_________.

符号语言：∵_____________________，∴ABCD为正方形.

2．正方形的判定一：_____________________________.关键词：________+_________.

符号语言：∵_________________，∴矩形ABCD为正方形.

3．正方形的判定二：_____________________________.关键词：________+_________. .

符号语言：∵_________________，∴菱形ABCD为正方形.

判定方面：

1.平行四边形：两组对边分别相等；两组对边分别平行；一组对边平行且相等；对角线互相平分；

2.矩形：三个直角+四边形；一个直角+平行四边形；对角线相等+平行四边形；

3.菱形：四边相等+四边形；邻边相等+平行四边形；对角线垂直+平行四边形；

4.正方形：一个直角+邻边相等+平行四边形；一个直角+对角线垂直+平行四边形；对角线相等+邻边相等+平行四边形；对角线相等+对角线垂直+平行四边形；

由此可见，正方形的判定是在平行四边形的基础之上加上矩形的一个特性和菱形的一个特性。

五、正方形性质的应用

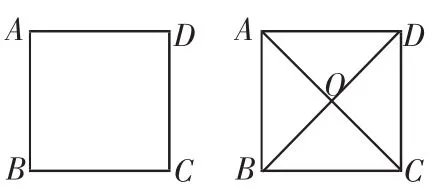
1．在正方形ABCD中，若AB＝2，则AD＝_____，BC＝_____，CD＝_____，BD＝_____，AO＝_____，AC＝_____，∠ABC＝_____°，△ABC是_____三角形，△OBC是_____三角形，S正方形ABCD＝_____．

2．下列叙述错误的是 （ ）

A．平行四边形的对角线互相平分

B．正方形的对角线互相平分且垂直

C．菱形的对角线相等

D．矩形的对角线相等

3．正方形具有而矩形没有的性质是 （ ）

A．对角线互相平分 B．对边相等

C．对角线相等 D．每条对角线平分一组对角

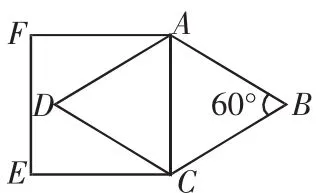
4．如图，菱形ABCD中，∠B＝60°，AB＝4，以AC为边长的正方形ACEF的周长为（ ）

A．14 B．15

C．16 D．17

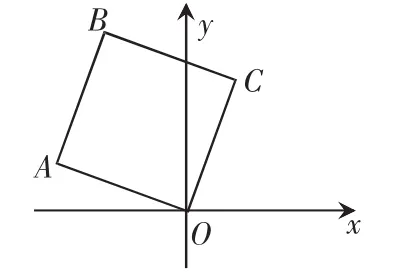
5．如图，在正方形OABC中，点A的坐标是（-3，1），点B的纵坐标是4，则B，C两点的坐标分别是 （ ）

A．（-2，4），（1，3）

B．（-2，4），（2，3）

C．（-3，4），（1，4）

D．（-3，4），（1，3）

六、正方形判定的应用

6．已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是

（ ）

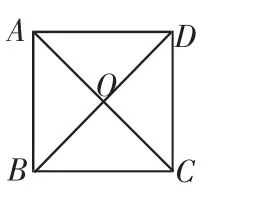
A．选①② B．选①③ C．选②④ D．选②③

7.已知：如图，在正方形ABCD中，点E、F、G、H分别在AB、BC、CD、DA上，且AE＝BF＝CG＝DH．

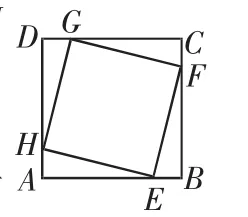
求证：四边形EFGH是正方形．

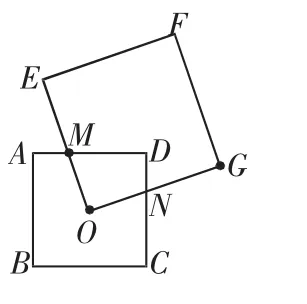
8．正方形ABCD的对角线交于点O，已知正方形OEFG从OA位置绕点O顺时针旋转（0°<旋转角<90°），OE、OG分别与AD、DC交于点M、N.（1）求证OM=ON；（2）四边形OMDN的面积变不变？说明理由.