基于BP神经网络的地铁车厢拥挤度预测方法*

方晨晨 周继彪 董 升 王依婷 陈莎雯

(1.武汉理工大学交通学院 武汉 430063；2.宁波工程学院建筑与交通工程学院 浙江宁波 315211； 3.同济大学交通运输工程学院 上海 201804)

0 引 言

地铁车厢拥挤度是反映城市轨道交通线网运行是否合理和服务质量优劣的重要指标，反映了地铁车站内实际承载客流和设计负荷之间的关系[1-3]。对地铁车厢拥挤度进行科学预测，一方面可以反映地铁车厢内的实际拥挤状态，避免客流高度集聚而发生踩踏现象；另一方面为城市轨道交通线路实行局部封站、限流等措施提供依据,因此，地铁车厢内拥挤度的预测对于实时调度和限流管控等具有重要意义。

准确、可靠的乘客拥挤度预测是轨道交通客流控制的前提和关键，是公共交通领域的热点研究内容之一[4-8]。预测结果可用于支持轨道交通运输系统管理，如轨道交通运营规划、车站内乘客监管规划和收益管理。目前客流预测方法主要包括宏观客流量预测法和微观客流量预测法[9-10]。在宏观客流量预测方面，主要方法有四阶段法、土地利用法、交通特征模型法等。此类方法的主要内容包括出行生成、出行分布、交通方式划分和交通分配等4个阶段，在工程项目领域发挥了巨大的作用，为管理部门提供了一定的科学数据。在微观客流预测方面，主要包括线性预测方法和非线性预测方法。其中，线性预测方法主要针对历史客流数据，在时间序列上进行客流平滑和预测。该种方法建模简单，但精度相对偏低。在非线性预测方法中，具体预测模型十分丰富，比较典型的方法主要有神经网络法、灰度预测法、移动网络预测法等。以上方法的特点就是计算量大、建模过程复杂，但是它的预测结果较为准确。如：Xie等[11]提出了一种基于神经网络和OD矩阵估计的方法，用于预测高速铁路系统的短期客流量。实验结果表明：所提出的方法在预测高速铁路短期客流方面表现良好；董升伟[12]针对BP神经网络的传递函数、训练算法进行了改进，结果表明改进的神经网络提高了预测精度；Huang等[13]提出了一种移动网络方法(mobility network approach)，引入异常移动网络的概念来区分异常移动通量与普通移动通量，用于识别和预测大型人群聚会中涉及的移动模式。研究发现：在异常的移动网络中，通常在最大人群密度之前几个小时，高压力人群密度之前的节点度已经超过临界阈值；Li[14]等利用多尺度径向基函数(multiscale radial basis function, MSRBF)网络，预测特殊事件情景下的地铁短时客流量。试验发现：该方法不仅比非常规需求预测的流行计算智能方法具有更好的预测性能，而且还利用网络知识来增强预测能力并查明易受攻击的地铁站以进行人群控制措施。

随着计算机运算速度和性能的提升，客流预测中又呈现出复合模型的趋势，同时结合线性模型和非线性模型的优势，以进一步提高预测模型的精度。如Wei等[15]开发了一种混合EMD-BPN预测方法，该方法结合了经验模式分解(empirical mode decomposition, EMD)和反向传播神经网络(back-propagation neural networks, BPN)来预测地铁系统中的短期客流。结果表明,混合EMD-BPN方法在预测短期地铁客流方面表现良好且稳定；Sun等[16]提出了一种基于wavelet-SVM混合模型的短时客流预测方法，结合了Wavelet和SVM模型的互补优势，并基于北京地铁系统的历史客流数据和多项标准进行了评估。结果表明,该混合方法具有最佳的预测性能；Wang[17]等通过季节性自回归综合移动平均模型捕捉乘客的固有周期性，提出了一种支持向量机整体在线模型(support vector machine overall online model, SVMOOL)，并基于南京地铁珠江路和三山街站5min的乘客量进行了验证。该类算法的最大特点就是将线性和非线性算法的优点进行组合并改进，不仅能够提高工作效率，而且预测精度也进一步提升。鉴于此，基于BP神经网络自身良好的学习性能、高度的非线性预测能力,以及地铁车厢乘客拥挤的特点，拟选用BP神经网络为基础工具对地铁车厢下车人数进行短时预测，并结合车厢立席密度实现乘客拥挤度预测，利用决定系数(R2)和平均相对误差(MRE)2个指标比较不同结构模型的误差精度。

1 基础数据调查

1.1 调查方案

通过采集各节车厢下车乘客数据，进行神经网络模型的训练和仿真实验，为预测模型构建提供基础。选取通勤客流(星期一至星期五)进行调查分析，以提高数据调查的准确性。调查工作日的高峰时段(17:00—18:00)地铁到达鼓楼站时，各班次列车中的各车门下车人数。

宁波地铁鼓楼站是一、二号线的换乘站，呈L形结构(见图1)，日均客流量相对较大，且换乘存在高差，站台人员走行、候车情况相对混乱。选取该站点为试验地点，并将数据采集点设置在轨道交通2号线站台(栎社国际机场方向)。同时为方便采集，不影响乘客的正常上下车，采用视频采集法对12个样本车门进行调查。

图1 数据采集点(地点：鼓楼地铁站，浙江宁波)Fig.1 Data collection location (Gulou SubwayStation, Ningbo, Zhejiang)

1.2 调查结果

根据现场实测结果，调查时间内鼓楼地铁站到站班次共为10个班次。调查时间连续5个工作日，得到50组有效数据，如图2所示。

由图2可见，工作日晚高峰时段的各车门下车人数随时间呈非线性变化，具有时变性和不稳定性，结果处于[0, 25]的范围内波动。

图2 调查结果Fig.2 Survey results

调查得到星期五第10班次列车即将到达鼓楼站前各节车厢已有人数，此数据用于车厢拥挤度标定，见表1。

表1列车即将到达鼓楼站前各节车厢已有人数

Tab.1NumberofpassengeratthetenthsubwaythatisarrivingatGulouStationonFriday

车厢号一二三四五六人数16586701122550

注：星期五第10班次。

2 地铁车厢拥挤度预测方法

2.1 车厢拥挤度基本内涵

车厢拥挤度是一种乘客在乘车过程中考虑了舒适度和安全性的心理感受，反映了乘客在乘车过程的服务质量和用户体验水平。在城市轨道交通规划设计中，立席密度是十分重要的设计参数，对车辆运能、乘客服务水平、拥挤程度评价等方面均有重要影响[5,6,18]。立席密度是指有效立席面积(除去坐席的面积)的乘客数，单位为人·m-2。合理的立席密度结合了乘客舒适度需求，此处地铁车厢拥挤度拟用合理的立席密度表示。一般情况下，地铁列车车辆定员规范[19]的标准定员为6人·m-2，超员为9人·m-2。以立席密度为依据，将车厢拥挤程度划分为满载、拥挤和舒适3个等级，如表2所示。

表2 车厢拥挤度划分标准

2.2 预测模型构建

2.2.1 BP模型构建

BP(back propagation)神经网络是一种具有连续传递函数的多层前馈人工神经网络，通过误差反向传播算法，并以均方误差最小化为目标不断修改网络的权值和阈值，最终能高精度地拟合数据[14]。BP神经网络具有较强的非线性拟合能力，广泛应用于非线性时间序列数据预测，并取得了良好的效果。BP神经网络结构如图3所示。

图3 神经网络基本原理Fig.3 Neural network theory

图5中各变量之间关系可通过式(1)和式(2)表示。

(1)

(2)

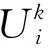
①初始网络模型构建，包括确定输入、输出层、隐含层层数、隐含层神经元个数及传输函数；②数据预处理；③神经网络模型训练；④测试精度满足要求后预测模型构建完成，如图4所示。

图4 BP神经网络实验流程Fig.4 Process of BP neural network experiment

数据预测模型构建基本思路为：以第1班次至第n班次地铁的各车厢下车人数预测第n+1班次的各车厢下车人数，再以第2班次至第n+1班次的数据预测第n+2班次数据，以此循环。经实际调查，鼓楼站晚高峰时段内共有10班次地铁。以前7班次作为输入层，第8班次作为输出层。考虑到不同输入数据会影响预测结果，分别将输入层设为6,7,8,9个班次进行实验，如图5所示。

图5 BP神经网络预测模型Fig.5 BP neural network prediction model

BP神经网络一般设置为输入层、单层隐含层及输出层的3层结构，由于与神经元个数相比，网络层数对预测结果影响较小，采用3层神经网络结构便于调整。隐含层的神经元个数会影响预测精度：当神经元个数较多时，会造成训练时间增加，训练集结果过于准确而验证集不准确的问题；当隐含层神经元个数太少时，不能建立合理的权重关系，使得网络预测不够准确。神经元个数的确定没有具体的标准，由各自的经验方法确定，为使构建的模型更精确，考虑不同神经元个数对预测结果影响，根据经验分别将神经元个数设置为6,7,8,9,10个。以图5为例，构建出7个输入数据10个神经元的3层BP神经网络初始模型。

传输函数采取S形函数logsig，可以将较大区域范围的数据映射到[0,1]范围内，可提高预测精度，输出层则采用线性函数purelin。采取traingdm作为反向传播的训练函数，traingdm具有网络训练功能，可根据动量梯度下降来更新权重和偏差值。

2.2.2 数据预处理

S形传输函数使函数输出控制在[0,1]之间，为使传输函数更好反应，将原始数据进行归一化处理，将数据控制在[0,1]之间，如式(1)所示。

(3)

2.2.3 车厢拥挤度标定

对即将到站地铁各车厢拥挤度预测，仅考虑即将到站列车车厢现有的乘客数，忽略到站时车厢的下车人数，会产生较大预测误差(如地铁到站前某节车厢为拥挤状态，而在到站时该节车厢乘客下车数量大，使该节车厢出现不拥挤的情况)。因此需结合车厢已有人数和预测得到的各车厢下车人数，进行车厢预计承载量计算。为得到每节车厢的预计承载量可采用式(4)～(6)计算。

(4)

Li=Xi-Ni

(5)

Mi=P-Li

(6)

结合表2车厢拥挤度划分标准及宁波B型地铁列车各车厢立席面积，可得各节车厢不同拥挤度下立席人数，如表3所示。以Li值与表3核对即可得第i节车厢处于拥挤度状态。已知B型列车每节车厢坐席人数为36人，相加得每节车厢不同拥挤度下的承载量，如表4所示。

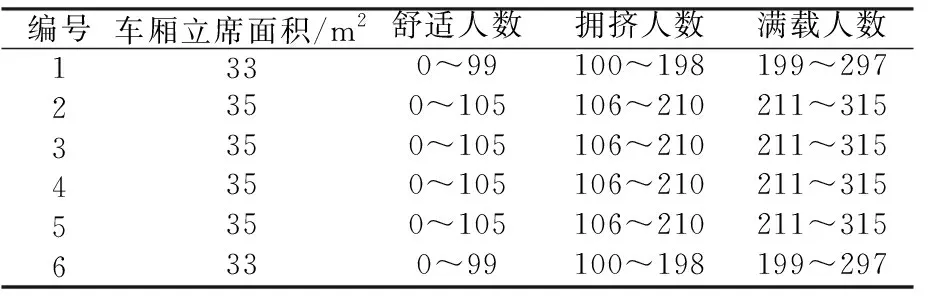
表3 各车厢拥挤度标定结果

表4 各车厢承载量计算结果

2.3 车厢拥挤度预测结果

以相对误差和决定系数为指标来评价网络预测性能的好坏，计算过程见式(7)～(8)。

(7)

R2=

由Matlab实验得到不同情况下各车门下车人数的预测值，通过式(7)和式(8)得到决定系数及平均相对误差(12个车门预测相对误差平均值)。将预测结果与真实值比较，得到不同结构模型的预测结果，如图6所示。

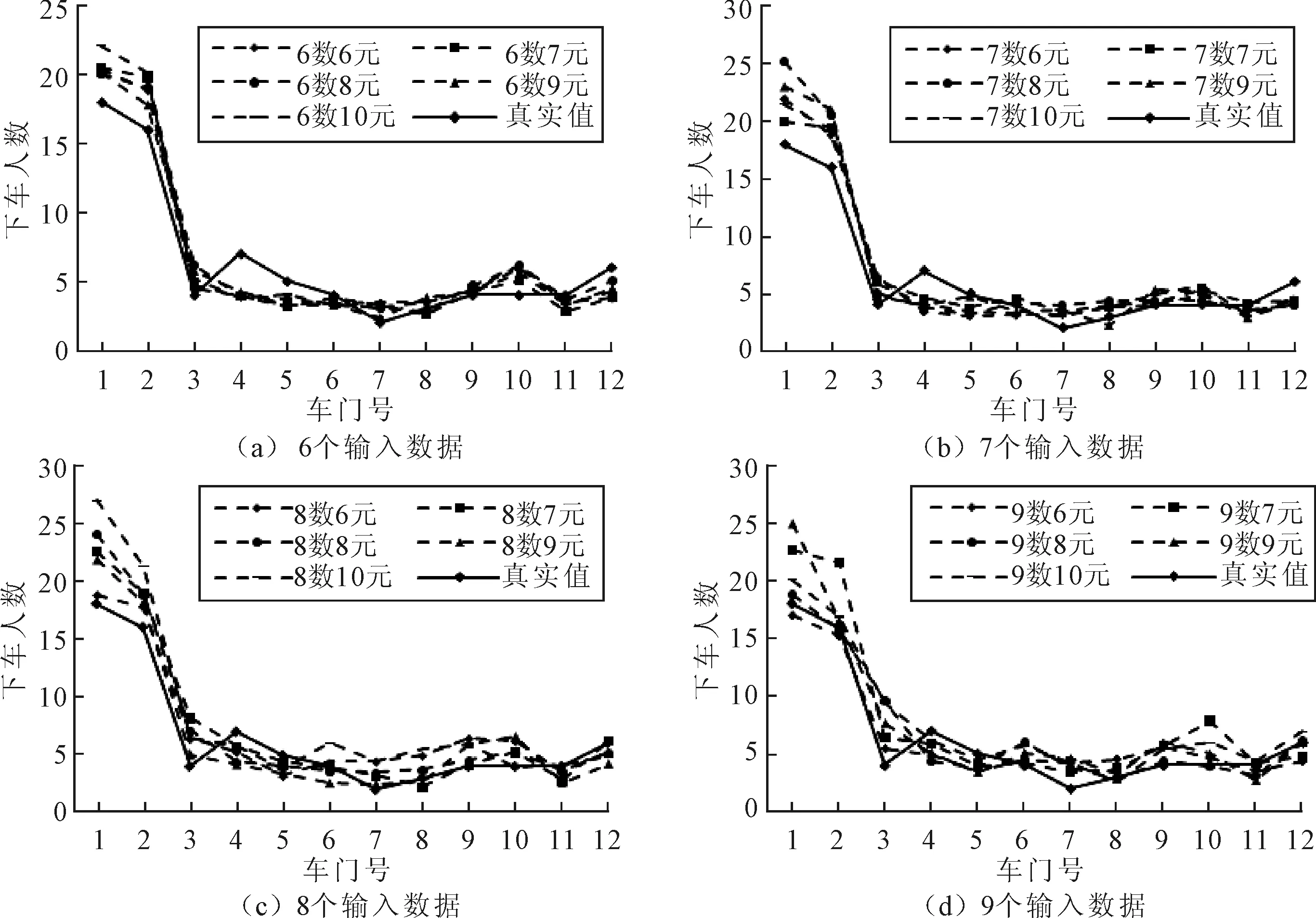
图6 不同结构模型预测结果对比Fig.6 Comparison of prediction results of different structural models

不同输入数据与不同神经元个数情况下(简称数元，如7个输入数据10个神经元为7数10元)的预测结果准确度对比，如图7所示。

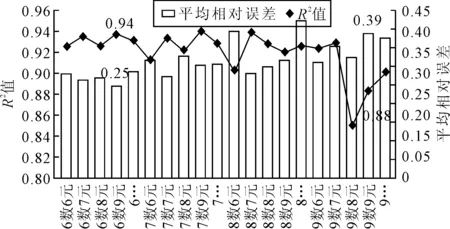
图7 不同结构模型预测误差对比Fig.7 Comparison of prediction errors of different structural models

由图7可见，在3层结构中6个输入数据9个神经元构成的BP神经网络决定系数R2为0.94，平均相对误差为0.25，综合分析其预测结果相对准确；而9个输入数据9个神经元构成的模型，由于输入数据太少，神经元之间不能建立合理的权重关系，预测精确度相对较低，决定系数R2为0.88，平均相对误差为0.39。其余结构模型的决定系数R2多数高于0.9，平均相对误差在0.3至0.35之间。在BP神经网络建模实验中，网络的权值和阈值会存在随机初始化的情况，预测结果也随之变化。

在实验中，各车门下车人数预测结果出现的最小绝对误差为0人，最大绝对误差为9人，取最佳预测结果及最差预测结果，利用式(4)～(6)计算车厢拥挤度，分别得到表5和表6。

表5 各车门下车人数最佳预测结果情况下车厢拥挤度预测结果

表6 各车门下车人数最差预测结果情况下车厢拥挤度预测结果

从表5和表6可得，各车门下车人数最佳和最差预测结果情况下，所得车厢拥挤度预测与实际均相同，下车人数预测数据与实际数据误差在允许范围内。

3 结束语

实验结果表明，BP神经网络预测地铁车厢各车门下车人数具有适用性；神经元的个数、输入数据个数与最终训练的输入数据量均对神经网络精确度产生影响；利用立席密度对车厢拥挤度的划分，不仅考虑了乘客舒适度，也符合轨道交通设计规范。通过BP神经网络对即将到站地铁车厢下车人数预测，实现的是对即将到站地铁车厢拥挤度预测，鉴于该场景下，仍可通过增加总训练数据量优化网络结构，使BP神经网络最终达到更为准确的预测要求。

当前对于提前获取地铁车厢拥挤度的研究及应用相对缺少。在提倡以人为本的公共交通出行环境下，使地铁乘客在相对拥挤的地铁站内得知自己所处环境的安全状态，根据实时信息引导乘客候车和疏散意义重大。在后续研究工作中将弥补数据量不够充分的问题，分别研究地铁不同车站、不同行车方向、不同运营时段等情况下BP神经网络预测的适用性。同时为了准确、快速、方便的获取乘客上下车人数以及到站前地铁车厢已有人数，视频监控自动识别统计研究将是另一个研究重点。另外，在车厢拥挤度预测的基础上，如何将预测信息及时准确地发布给候车乘客也有待进一步研究。