非线性极小极大问题的分数阶粒子群算法

李昌兴, 徐 迈, 惠莉萍

(1.西安邮电大学 理学院， 陕西 西安 710121; 2.西安科技大学 理学院， 陕西 西安 710054)

非线性极小极大问题(nonlinear minimax problem, NMP)是一类典型的非可微优化问题，在工程优化设计、电子线路优化设计、计算机辅助几何设计、最优控制及对策论中有着广泛应用。工程实际中很多问题，如非线性L1、L∞拟合问题和非线性方程组求解，都可以转化成极小极大问题的数学模型。

将信息论中的熵概念引入函数优化领域，由此得出的极大熵函数转化方法[1]可将非光滑问题转化为光滑优化问题，利用经典优化方法，如信赖域法、拟牛顿法、共轭梯度法、SQP方法等[2-6]，求解光滑优化问题，即可得到非光滑问题的近似最优解。然而，这些传统优化方法的计算效率受初始点的选取影响比较大，且大多算法都要使用目标函数的梯度信息，这就给问题的求解带来了困难。

智能优化算法不需要使用函数的梯度信息和初始点，计算效率较高。其中，粒子群算法(particle swarm optimization，PSO)[7]的原理较为简单且程序容易实现，目前已被广泛应用于数值优化、神经网络训练、数据挖掘和系统控制等领域。

对于非线性极小极大问题，可结合改进的粒子群算法与极大熵函数求解[8]，也可结合差分进化算法与极大熵函数法求解[9]，或者结合粒子群-邻近点混合算法和极大熵函数法求解[10]。但是，粒子群算法是一种依概率收敛的随机优化算法，对多峰多谷的复杂优化问题，易陷入局部最优。基于分数阶速度的粒子群算法(PSO with fractional-order velocity，FOPSO)使用分数阶微分的定义，改进了粒子群算法的速度更新公式[11]，相较于经典粒子群算法，收敛速度更快。

本文将针对极小极大问题中，极大值函数不可微的特点，先用极大熵函数法将目标函数转化成可微函数，再利用分数阶粒子群算法求解可微的近似优化问题。

1 极大熵函数法

考虑无约束优化问题

利用极大熵函数法，可将无约束非线性极小极大问题转化为光滑函数的无约束优化问题。极大熵函数定义为[4]

(1)

其中，p≥1为控制参数，Fp(x)即为函数f(x)在变量x∈n上的极大熵函数。

对于有限值p，Fp(x)是可微的，且式(1)可以改写为[4]

由此可得

函数Fp(x)的值随着参数p的增加而单调减小，且当p趋于无穷大时，Fp(x)以f(x)为极限，即

在实际数值计算时，只要参数p取得足够的大，就可以使用极大熵函数Fp(x)代替不可微目标函数f(x)，从而可将原来的非线性极小极大问题的求解转化为一个易于求解的可微函数的无约束优化问题。

2 分数阶粒子群算法

分数阶微积分(fractional calculus，FC)是数学分析的一个分支，也是应用科学中的数学工具之一。它是经典微积分的自然延伸，其微分算子及积分算子的阶数可扩展到实数或复数范围。换言之，分数阶微积分是传统积分和微分的泛化，它将非整数值包含到导数或者积分的幂中。因可用于大量自然现象的精确描述，分数阶微积分已被成功应用于诸多科学领域，如工程科学、计算数学和流体力学等。事实上，针对服务于建模、曲线拟合、滤波、模式识别和边缘检测等应用的众多算法，分数阶微积分为提高其稳定性、可控性、可观察性和鲁棒性等性能，发挥着重要作用。

一元函数x(t)的Grünwald-Letnikov分数阶微分定义为

(2)

其中，α∈(0,1]，Γ(·)是伽玛函数。

式(2)揭示：虽然整数阶导数仅仅意味着有限序列，但分数阶导数需要无限多项；整数导数是“局部”运算符，与此相反，分数阶导数毫无疑问地包含了过去所有事件的“记忆”。

式(2)的近似表达式为

(3)

其中，T是采样周期，r是截断次序。

分数阶模型具备固有的记忆特性，非常适合描述诸如不可逆性和混沌现象。据此可知，分数阶微积分工具非常适合描述粒子轨迹的动态现象。使用分数微积分，可以控制粒子群优化算法的收敛速度。

为了修改速度导数的阶数，需要重新排列粒子群算法的原始速度方程

vt+1=vt+φ1(pbest-x)+φ2(gbest-x),

(4)

该表达式可以重新写为

vt+1-vt=φ1(pbest-x)+φ2(gbest-x)。

(5)

式(5)左侧的vt+1-vt是阶数α=1(假设T=1)时微分的离散形式，故有

Dα[vt+1]=φ1(pbest-x)+φ2(gbest-x)。

(6)

如果考虑分数微积分的特点，速度微分的阶数可以推广为实数α∈[0,1]，这样可以获得更平滑的变化和更长的记忆效应。考虑表达式(3)给出的微分的第一个r=4项，表达式(6)可改写为[11]

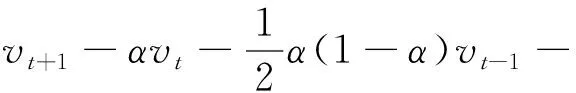
当r≥4时，实验测试可得相似结果。

实验测试中，根据表达式

α的值从0.9到0.4线性变化。其中，t为当前迭代次数，而最大迭代次数IM=5 000。

3 结合极大熵的分数阶粒子群算法

将极大熵函数法和分数阶粒子群算法相结合，给出一种解决非线性极小极大问题的新算法。

3.1 粒子群速度更新公式的改进

选用速度更新公式[11]

(7)

位置更新公式不变，仍为

xt+1=xt+vt+1。

(8)

3.2 算法步骤

步骤1对每个粒子初始化，确定粒子群规模N、加速常数c1和c2、问题维数d、最大迭代次数IM、问题的位置和速度的上下限，并随机产生N个初始位置和N个初始速度。

步骤2将极大熵函数代替原目标函数作为适应度值函数，计算每个粒子的适应度值vf。

步骤3对每个粒子，若粒子的适应度值vf优于历史的个体最优位置Pi的适应度值，则将当前适应度值设置为个体极值Ibest，当前位置为个体最优位置Pi。

步骤4对每个粒子，若粒子的适应度值vf优于历史的全局最优位置Pg的适应度值，则将当前适应度值设置为全局极值Gbest，当前位置为全局最优位置Pg。

步骤5根据公式(7)，更新粒子的速度，并将其限制在Vmax内。

步骤6根据公式(8)，更新粒子的位置，并将其限制在[Xmin,Xmax]内。

步骤7如果达到终止条件，则输出问题的解；否则更新迭代次数，并转到步骤2。

3.3 重要说明

(1) 在转化极大熵函数时，由于要求p的值足够大，所以计算机在计算时易导致epfi(x)发生数据溢出，故在计算时采用与文献[8]中相同的计算技巧来避免数值溢出。

(2) 对于较为复杂的非线性极小极大问题，将粒子群规模取大以达到避免早熟收敛的目的。

4 数值实验

取参考文献[5-6，8，12-15]中的8个非线性极小极大问题做测试。

问题1(Charalambous-Conn 2问题)

参数n=2,m=3。

f2(x)=(2-x1)2+(2-x2)2,

f3(x)=2e(-x1+x2)。

问题2(Charalambous-Conn 1问题)

参数n=2,m=3。

f2(x)=(2-x1)2+(2-x2)2,

f3(x)=2e(-x1+x2)。

问题3参数n=2,m=3。

f2(x)=sinx1,f3(x)=cosx2。

问题4参数n=3,m=6。

f3(x)=x1+x2+x3-1,

f4(x)=x1+x2-x3+1,

问题5(Wong1问题) 参数n=7,m=5。

f1(x)=(x1-10)2+5(x2-12)2+

f3(x)=f1(x)+10(7x1+3x2+

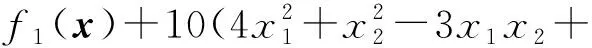
问题6参数n=3,m=30。

fi(x)=-fi-15(x)(i=16,17,…,30)。

ui=i,vi=16-i,wi=min{ui,vi},y=(y1,y2,…,y15)= (0.14,0.18,0.22,0.25,0.29,0.32,0.35,0.39, 0.37,0.58,0.73,0.96,1.34,2.10,4.39)。

问题7(Demyanov-Malozemov问题)

参数n=2,m=3。

f1(x)=5x1+x2,f2(x)=-5x1+x2,

问题8(Rosen-Suzuki问题)

参数n=4,m=4。

5x2-21x2+7x4,

x1-x2+x3-x4-8),

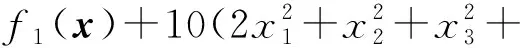
2x1-x2-x4-5)。

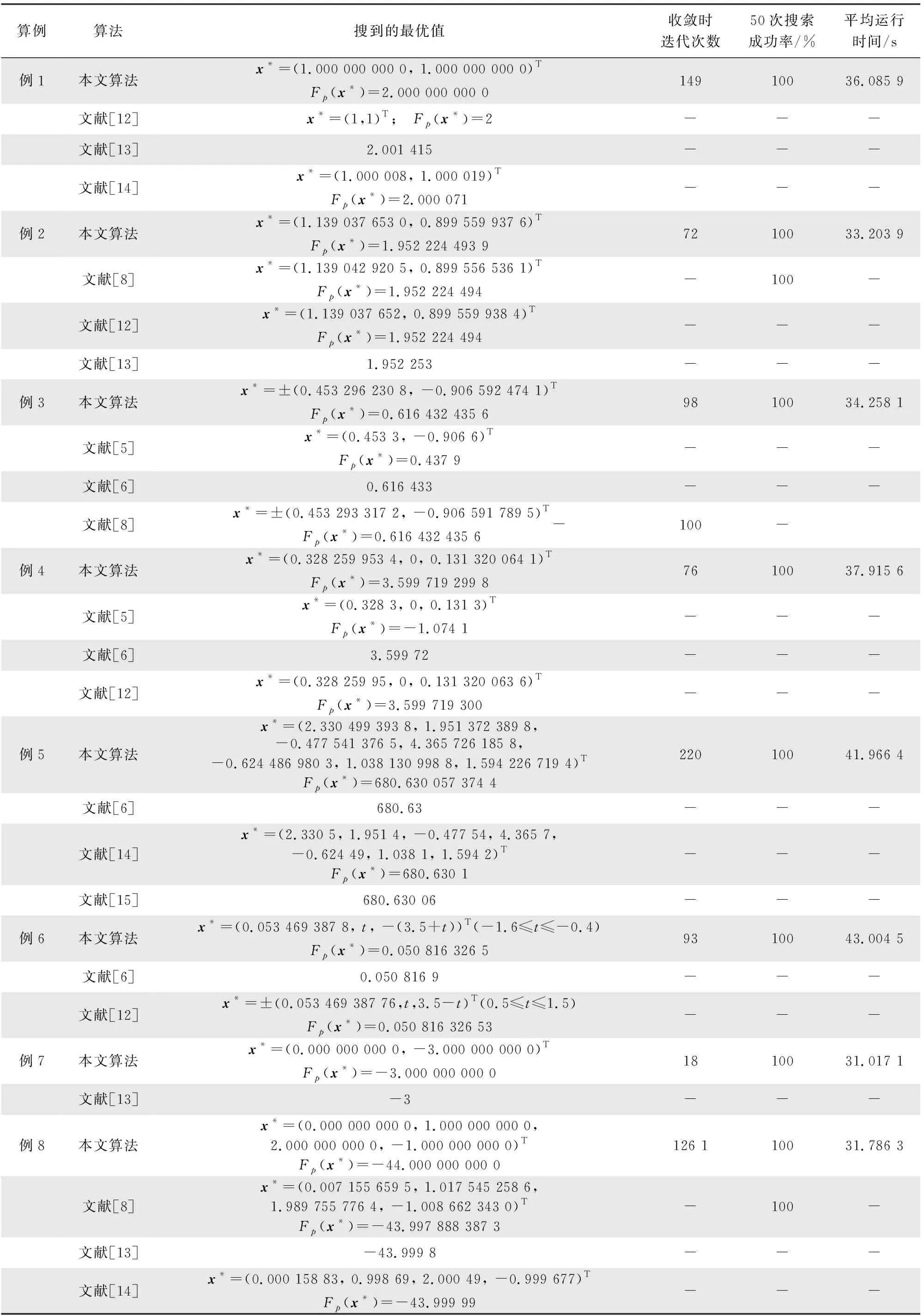
在主频为2.80 GHz的windows10系统下，使用MATLAB R2014a软件进行仿真实验，算法执行50次，各问题的最优解迭代过程和50次运行结果变化分别如图1和图2所示。相关参数设置如下：控制参数p的值设置为105；加速常数c1=c2=1.449 45；粒子群规模为500；最大迭代次数为5 000；最大速度为2；粒子搜索范围根据问题变化，问题1、问题2和问题8的搜索范围为[-2,2]，问题3和问题4的搜索范围为[-1,1]，问题5的搜索范围为[-5,5]，问题6的搜索范围为[-4,4]，问题7的搜索范围为[-3,3]。计算结果和平均运行时间见表1。

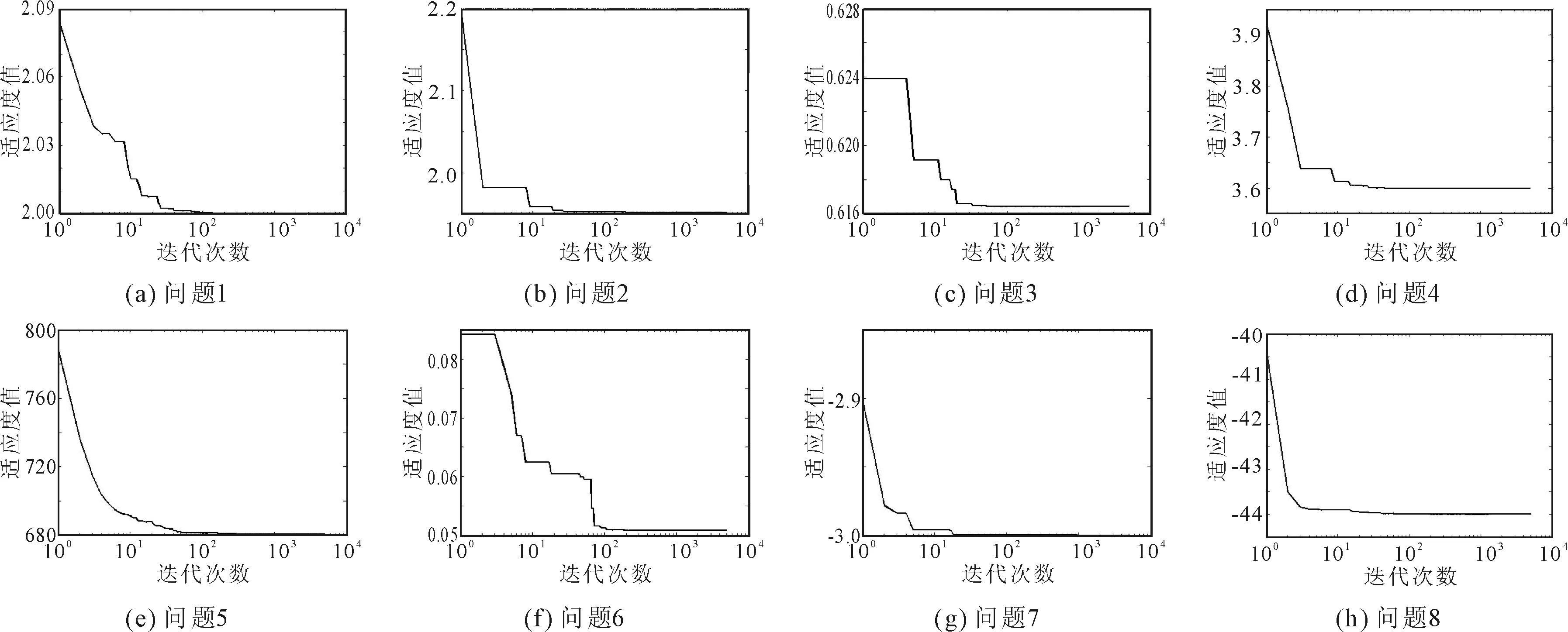
图1 各问题的最优解迭代过程

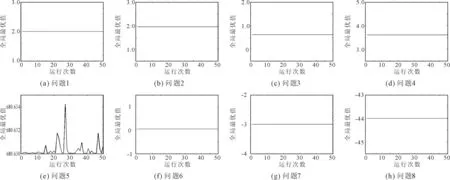
图2 各问题50次运行结果变化

算例算法搜到的最优值收敛时迭代次数50次搜索成功率/%平均运行时间/s例1本文算法x*=(1.000 000 000 0, 1.000 000 000 0)TFp(x*)=2.000 000 000 014910036.085 9文献[12]x*=(1,1)T; Fp(x*)=2---文献[13]2.001 415---文献[14]x*=(1.000 008, 1.000 019)TFp(x*)=2.000 071---例2本文算法x*=(1.139 037 653 0, 0.899 559 937 6)TFp(x*)=1.952 224 493 97210033.203 9文献[8]x*=(1.139 042 920 5, 0.899 556 536 1)TFp(x*)=1.952 224 494-100-文献[12]x*=(1.139 037 652, 0.899 559 938 4)TFp(x*)=1.952 224 494---文献[13]1.952 253---例3本文算法x*=±(0.453 296 230 8, -0.906 592 474 1)TFp(x*)=0.616 432 435 69810034.258 1文献[5]x*=(0.453 3, -0.906 6)TFp(x*)=0.437 9---文献[6]0.616 433---文献[8]x*=±(0.453 293 317 2, -0.906 591 789 5)TFp(x*)=0.616 432 435 6-100-例4本文算法x*=(0.328 259 953 4, 0, 0.131 320 064 1)TFp(x*)=3.599 719 299 87610037.915 6文献[5]x*=(0.328 3, 0, 0.131 3)TFp(x*)=-1.074 1---文献[6]3.599 72---文献[12]x*=(0.328 259 95, 0, 0.131 320 063 6)TFp(x*)=3.599 719 300---例5本文算法x*=(2.330 499 393 8, 1.951 372 389 8,-0.477 541 376 5, 4.365 726 185 8,-0.624 486 980 3, 1.038 130 998 8, 1.594 226 719 4)TFp(x*)=680.630 057 374 422010041.966 4文献[6]680.63---文献[14]x*=(2.330 5, 1.951 4, -0.477 54, 4.365 7, -0.624 49, 1.038 1, 1.594 2)TFp(x*)=680.630 1---文献[15]680.630 06---例6本文算法x*=(0.053 469 387 8, t, -(3.5+t))T(-1.6≤t≤-0.4)Fp(x*)=0.050 816 326 59310043.004 5文献[6]0.050 816 9---文献[12]x*=±(0.053 469 387 76,t,3.5-t)T(0.5≤t≤1.5)Fp(x*)=0.050 816 326 53---例7本文算法x*=(0.000 000 000 0, -3.000 000 000 0)TFp(x*)=-3.000 000 000 01810031.017 1文献[13]-3---例8本文算法x*=(0.000 000 000 0, 1.000 000 000 0,2.000 000 000 0, -1.000 000 000 0)TFp(x*)=-44.000 000 000 0126 110031.786 3文献[8]x*=(0.007 155 659 5, 1.017 545 258 6,1.989 755 776 4, -1.008 662 343 0)TFp(x*)=-43.997 888 387 3-100-文献[13]-43.999 8---文献[14]x*=(0.000 158 83, 0.998 69, 2.000 49, -0.999 677)TFp(x*)=-43.999 99---

由图1和图2可见，本文算法收敛快(收敛时迭代次数见表1)、稳定性好。由表1可见，本文算法的计算结果整体优于文献[5-6，8，12-15]中的结果。

对于例1，搜索得到的最优解2就是已知的精确解，与文献[12]的结果相同，比文献[13]的结果2.001 415和文献[14]的结果2.000 071都要精确；对于例2，本文搜索得到的最优解1.952 224 493 9比文献[8]的结果1.952 224 494 0、文献[12]的结果1.952 224 494和文献[13]的结果1.952 253都要好；对于例3，本文搜索得到的最优解0.616 432 435 6与文献[8]的结果0.616 432 435 6相同，比文献[5]的结果0.437 9准确，比文献[6]的结果0.616 433更好；对于例4，本文搜索得到的最优解3.599 719 299 8比文献[5]的结果-1.0741准确，比文献[6]的结果3.599 72和文献[12]的结果3.599 719 300都要好；对于例5，本文搜索得到的最优解680.630 057 374 4比文献[6]的结果680.63、文献[14]的结果680.630 1和文献[15]的结果680.630 06都要好；对于例6，本文搜索得到的最优解0.050 816 326 5比文献[6]的结果0.050 816 9和文献[12]的结果0.050 816 326 53都要好；对于例7，本文搜索得到的最优解-3与文献[13]的结果-3一样；对于例8，本文搜索得到的最优解-44是已知精确解，比文献[8]的结果-43.997 888 387 3、文献[13]的结果-43.999 8和文献[14]的结果-43.999 99都更好。

5 结语

本文针对极小极大问题中极大值函数不可微以及智能优化算法不需要使用函数的梯度信息和初始点的特点，提出了一种将分数阶粒子群算法与极大熵函数法相结合的新算法来解决非线性极小极大问题。首先利用极大熵函数法将目标函数转化成可微的函数；其次利用分数阶粒子群算法求解可微的近似优化问题。数值实验结果表明，本文提出的算法是一个可以解决非线性极小极大问题的有效算法。