拉格朗日对偶在大规模MIMO通信系统中的应用

何 华, 姜 静

(西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

在大规模多输入多输出(multiple-input multiple-output, MIMO)多用户通信系统中，波束形成是提高能效的重要方法[1]，在多用户下行波束形成中常常需要满足一定阈值下的信干噪比、信漏噪比等系统性能指标，并且在满足这些性能指标时需保证发射功率最小[2]。因此，大规模MIMO下行多用户的波束形成问题可表述为一般优化问题[3-4]，若能将该波束形成优化问题转化为凸优化问题，就能够方便问题分析，使之得到快速解决[5]。

凸优化问题是优化问题中最大的子类，具备有效的解决方案[6]，因此，凸优化方法已经广泛地应用在许多工程优化问题中。文献[7]将凸优化应用在MIMO雷达滤波器组的设计。文献[8]将凸优化应用在分集稀疏信号的重建。文献[9]将凸优化应用在无线传感器网络中的节点定位中。近年来，凸优化问题相关的理论、算法和软件工具发展迅速，已成为较成熟的处理工程应用问题的重要方法[10]。一旦实际问题被表述为凸优化问题，可认为该问题已经被解决[11]，就只是一项计算技术了[12]。

本文将凸优化应用到处理大规模天线系统的问题中，首先介绍了一种拉格朗日对偶理论和方法，该方法为非凸问题向凸问题的转化提供了途径，其次利用拉格朗日对偶方法详细分析了将大规模MIMO波束形成优化问题转化为凸优化问题的过程，使得大规模MIMO下行多用户波束形成优化问题得以解决。

1 拉格朗日对偶

常见的优化问题可表述为

Minf0(x),

(1)

s.t.fi(x)≤0(i=1,2,…,m),

hi(x)=0(i=1,2,…,p)。

其中，f0(x)是优化问题(1)的目标函数，fi(x)≤0与hi(x)=0分别是优化问题(1)的约束条件。

定义q*是问题(1)的全局最小值。x是优化问题(1)的变量，则该优化问题并不一定是凸的。

为了进一步解决该优化问题，引入参数变量

μ={u1,u2,…,um}∈m,λ={λ1,λ2,…,λm}∈m,

可得到拉格朗日方程

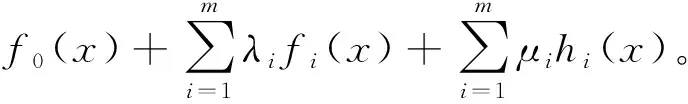
(2)

式(2)的对偶方程可表述为

g(λ,μ)=minL(x,λ,μ)。

(3)

对含有参数λ、μ的一组线性方程L(x,λ,μ)求最小，g(λ,μ)总是凹的。当λ≥0和g(λ,μ)有限时，对于原问题(1)总是存在f0(x)≥g(λ,μ)。则g(λ,μ)可认为是原问题(1)目标函数值的最小极限值，因此可得

q*=g(λ,μ)。

q*的最小极限值可由优化问题

maxg(λ,μ),

(4)

s.t.λ≥0,μ∈。

的对偶优化问题来处理。因为问题(3)总是凹的[4]，因此，无论原问题(1)是否为凸的，优化问题(4)总是凸的。

定义问题(4)的最大优化目标值为p*，则有q*≥p*。对绝大部分凸优化问题来说，满足q*=p*的强对偶关系。

2 在大规模MIMO通信系统中的应用

波束形成是大规模MIMO多用户通信系统中解决用户间干扰、提高能量效率和频谱效率的有效途径。考虑一个配置Nt根天线的大规模天线系统，在系统共有K个用户，每个用户配置1根天线，如图1所示。

图1 多用户大规模MIMO系统

基站端的发送信号为

其中：xm为基站向用户m传送的发射信号矩阵，wm为用户m的波束形成矩阵，S(t)是基站端的发射信号矩阵。

用户m的接收信号为

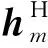
在波束形成是大规模MIMO多用户通信系统中，信漏噪比(signal-leakage-noise-rate, SLNR)即用户m的信号泄漏到其他用户的比例需限制在一定范围内，并且在该限制条件下，必须满足发射端的发射功率最小。上述问题可表述为如下优化问题

(5)

式中βk是用户m泄漏到用户k的信漏噪比所必须满足阈值条件。

显然，问题(5)不是凸优化问题，不能直接使用凸优化方法来解决该问题。为此，期望利用拉格朗日对偶法，将问题(5)转化为凸优化问题。

引入参数λ，得到问题(5)的拉格朗日方程

(6)

式(6)的对偶函数为

g(λ)=minL(wi,λi)。

(7)

容易看出，一般情况下

(8)

不一定是半正定矩阵。但是，存在一系列wi值可使得对偶方程g(λi)=-∞。

若考虑到λi是最大化g(λi)所对应的参数，则式(8)应当是半正定的。原问题(5)可表述为

(9)

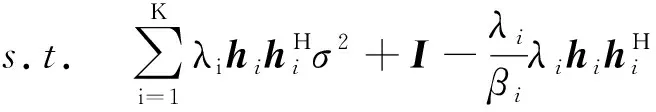
可见，大规模MIMO下行波束形成的信漏噪比优化问题就转化为形如公式(9)的凸优化问题，因此，可以利用基于凸优化的相关算法对问题(9)进行求解。

3 结语

把拉格朗日对偶方法应用于大规模MIMO多用户系统中波束形成优化问题中。首先，将大规模MIMO通信系统的下行波束形成表述为一般优化问题，然后，利用拉格朗日对偶将一般的优化问题转化为凸优化问题。对于具体大规模MIMO多用户通信系统，可以选择一种基于凸优化的方法对该系统进行定量分析与计算。因此，本文所给出的方法，为大规模MIMO通信系统的下行波束形成问题提供了一种途径。