基于多中心性加权的Ad hoc网络连通支配集算法

黄庆东, 郭 欢, 曹丽霞

(西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

Ad hoc网络是一种典型的无线自组织网络，其拓扑路由管理和维护十分复杂但又至关重要[1-3]。连通支配集(connected dominating set，CDS)是构建虚拟骨干网的一种方式[4]，能简化网络拓扑结构，快速开展路由，减少通信开销[5-6]。通过连通支配集算法实现网络高效管理，广受关注。

基于层次图的连通支配集算法[7]，结合贪心策略，可快速构建支配集，但简化拓扑效果并不明显。剪枝的连通支配集算法(2Rules-CDS算法)利用两种缩减规则改善拓扑结构[8]，其进一步改进(3Rules-CDS算法)[9]，可使所得CDS规模最优，且能解决生成连通支配集时存在的完全NP难问题。不过，这些算法局限于网络单一影响因素，以生成最小连通支配集为目的，忽略了全网负载均衡性。

为改善最小连通支配集负载不均衡问题，本文拟结合加权方式[10]和网络中心性[11]，给出一种基于中心性加权的连通支配集算法。融合多中心性计算网络节点的权值，选取最大者为支配节点，再选其一跳邻居中链路多者为支配邻居，分布式完成支配集构建，并对支配集的连通性进行判断和维护。

1 网络模型和加权公式

1.1 网络模型

Ad hoc网络模型可简单抽象为图论中无向连通图G=(V,E)，V是G的顶点集，表示网络中的节点集(包含|V|=K个元素)，E是G的边集，表示节点之间能直接通信的链路集。图谱论中表征节点连接关系的邻接矩阵定义为A=[akq]K×K，若节点k与节点q相连(q∈Nk，Nk表示节点k的邻居开集)，则元素akq=1，反之akq=0。

1.2 网络中心性加权公式

连通支配集，指网络中一个连通的子网。网络任一节点存在两种状态，或者在这个子网中，或者与这个子网中的节点相邻。在Ad hoc网络中，连通支配集被广泛用于构建虚拟骨干网，其支配节点长期处于消息处理和转发的工作状态，而支配邻居则定期进入休眠状态，能耗远大于被支配节点。选择性能优良的节点充当支配节点对于更好地管控整个网络非常关键。基于网络拓扑理论，考虑以下影响因素。

(1) 度中心性

节点的度是指其周围邻居节点的个数。节点的度体现了节点在网络中的局部位置特性。选取度较大的节点作为支配节点，可获得较小支配集。由于支配节点比其他节点承担更多通信任务，支配邻居过多易导致支配节点负载过重而出现信息拥堵，使负载不均衡而降低网络寿命，因此,度中心性(degree centrality，DC)是影响支配节点选取的重要因素[11]。定义节点k的度中心性为

cD(k)=|Nk|。

(1)

其中，|Nk|表示节点k一跳范围内的邻居数。

(2) 特征矢量中心性

某节点的邻居节点越多，且各邻居节点所连接的邻居节点越多，则该节点的影响力越大，其特征矢量中心性(eigenvector centrality，EC)值越高。区别于度中心性仅考虑一跳范围内节点的局部影响力，特征矢量中心性旨在衡量节点对网络的整体影响，可作为选取支配节点的关键因素[12]。节点k的中心性值cE(k)满足

其中α为归一化因子，akq为邻接矩阵A的元素值，且只有在节点k和节点q存在链路时为1，其余为0。设C是所有节点特征矢量中心性值构成的向量，则有向量形式

αC=AC。

(2)

可见，C为邻接矩阵A的特征向量。

由Perron-Frobenius定理可知，矩阵A存在一个由最大特征值α对应的最大特征向量，即特征矢量中心性向量C。

(3) 紧密中心性

紧密中心性(closeness centrality，CC)代表一个节点与网络中其他节点距离的大小程度[11]。若一个节点越接近网络中心位置，则该节点与其他节点距离越短，越紧密，CC值越大。根据距离因素选取网络中心位置的节点作为支配节点，可使支配集更优。定义节点k与网络中其他所有节点距离的平均值dk为

其中，dkq为节点k和节点q之间的距离，K表示网络的节点总数。则节点k的紧密中心性为

(3)

可见，dk越小，节点k越接近其他节点，则该节点的紧密中心性越大。

表征局部影响的度中心性、全网拓扑影响的特征矢量中心性、基于距离影响的紧密中心性，对网络支配节点的选取产生不同程度的影响。通过加权方式综合3种因素，定义节点k的中心性加权公式

W(k)=λ1cE(k)+λ2cD(k)+λ3cC(k)。

(4)

其中，λ1、λ2和λ3分别代表着各因素的相对重要性(λ1+λ2+λ3=1)，哪个因素越重要，其相对的权重因子值越大。在支配集构建过程中，优先选择权值W(k)大的节点为支配节点。

2 基于中心性加权的连通支配集算法

大多数连通支配集算法仅考虑构建最小连通支配集，忽略了网络负载均衡性。这些算法中的支配集可能会因通信任务繁重而迅速消耗自身能量，导致整个网络隔断。利用中心性加权公式可得出一种新的连通支配集生成算法。

2.1 连通支配集算法

步骤1以随机的方式在一定区域范围内依次抛撒K个节点并编号，且标记为初始状态，形成通信半径为r的初始化连通网络拓扑。

步骤2由式(1)、式(2)、式(3)分别计算初始拓扑中所有初始节点的度中心性值、特征矢量中心性值和紧密中心性值。

步骤3根据度中心性、特征矢量中心性和紧密中心性在网络中的影响程度，给权重因子分配适当数值，结合步骤2，通过式(4)计算每个初始节点的权值，并按从大到小的顺序排序。

步骤4选取最大值的初始节点标记为第一个支配节点。

步骤5将其一跳范围内连通效果较好的节点标记为支配邻居状态。

步骤6再从剩余初始节点中选择权值最大的作为下一个支配节点。

步骤7继续执行步骤5到步骤6，依次遍历拓扑中所有节点。

2.2 支配集连通性维护

由于Ad hoc网络拓扑动态可变，为维护支配集的连通性，保证网络的可靠性和稳定性，有必要引入可达性矩阵[13]。

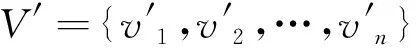
(5)

则图G′的可达性矩阵可记为P(G′)=[pkq]n×n。根据图G′的邻接矩阵A(G′)计算

(6)

其中，l表示迭代次数。

将Q(G′)的非零元素改为1，而零元素不变，变换后的矩阵即为可达性矩阵。

利用所得可达性矩阵对支配集的连通性进行判断，并选取最少连接节点维护支配集连通性。

步骤1执行连通支配集生成算法，得到n个支配节点，构成支配集。

步骤2由式(5)和(6)计算得到可达矩阵，并判断该支配集是否连通：若矩阵中不包含零元素，则表示该支配集连通；否则不连通，需要从所有非支配集中选取权值最大的节点，标记为临时连接节点，并添加到支配集中，形成新的支配集。

步骤3根据可达矩阵判断所得支配集是否连通：若连通，则标记临时连接节点的状态为连接节点，选取完成；若不连通，则重新选取权值次大的节点作为临时连接节点，以此类推。

步骤4若一个连接节点无法满足支配集连通，则需要添加多个连接节点来维护其连通性。默认将第一个连接节点添加到支配集中，重复上述步骤进行下一连接节点选取，直至网络中所有支配节点连通。

通过对生成的支配集进行连通性维护，形成由连通支配集构建的虚拟骨干网，可使骨干节点和非骨干节点分布更均衡，进而延长网络生命周期，保障网络高效地开展路由，完成节点之间数据的发送、接收和转发。

通过引入无线通信能耗模型[14]，可证实所给算法能够延长网络生命周期。

3 仿真及结果分析

为了验证所提算法的性能，采用MATLAB软件平台进行仿真研究，并与2Rules-CDS算法以及3Rules-CDS改进算法进行对比。

构建一个随机网络拓扑图，在归一化二维空间随机分布K个相同的网络节点，并预置欧氏距离r。若任意两节点间的通信距离皆小于r，则各节点间有边相连，形成无向连通拓扑图。应用所给算法、2Rules-CDS算法和3Rules-CDS算法，分别取网络节点为20个、30个、40个、50个和60个，各自重复实验100次，计算产生的支配节点数、网络负载均衡性和网络中每个节点平均剩余能量，并求其平均值作为实验结果。

当归一化距离r=0.6时,由3种算法得到的支配集规模曲线如图1所示。

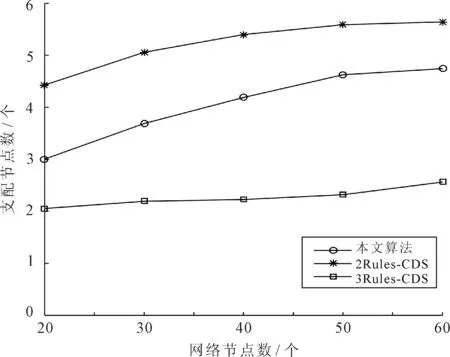
图1 支配节点规模对比

从中可见，随着网络节点数的增加，3种算法得到的支配节点数都有一定增长，但增长速度比网络节点数的增长速度小。本文算法所得支配节点数优于2Rules-CDS算法，而次于3Rules-CDS算法。这是因为3Rules-CDS算法以得到最小连通支配集为目的，忽略了网络负载均衡性；本文算法既优化了连通支配集规模，对负载均衡也有所改善。

定义负载均衡因子[15]

(7)

其中，n表示支配节点数，μd表示支配节点d的支配邻居数，v表示各支配节点的平均邻居节点数，即

其中K表示网络中节点个数。

负载均衡因子值F越大，表示网络负载均衡性越优良，即整个网络的支配节点数和支配邻居数分布更均衡，从而可延长网络生命周期。

负载均衡性随网络节点数的变化趋势如图2所示，随着网络节点数的增加，3种算法的网络负载均衡性皆呈下降趋势。这是因为，CDS算法在节点密集部署的监测环境中，拓扑结构更加复杂，节点间通信链路增多，会造成链路之间互相干扰变大，使负载均衡性下降。本文算法的网络负载均衡性之所以高于其他两种算法，是因为所给算法通过度中心性、特征矢量中心性和紧密中心性三方面加权选取权值最大的节点作为支配节点，其邻居节点中连通性好的为支配邻居，依次迭代，完成连通支配集的构建，使得网络中支配节点数目和支配邻居节点数目分布更合理，故能提高网络负载均衡能力。

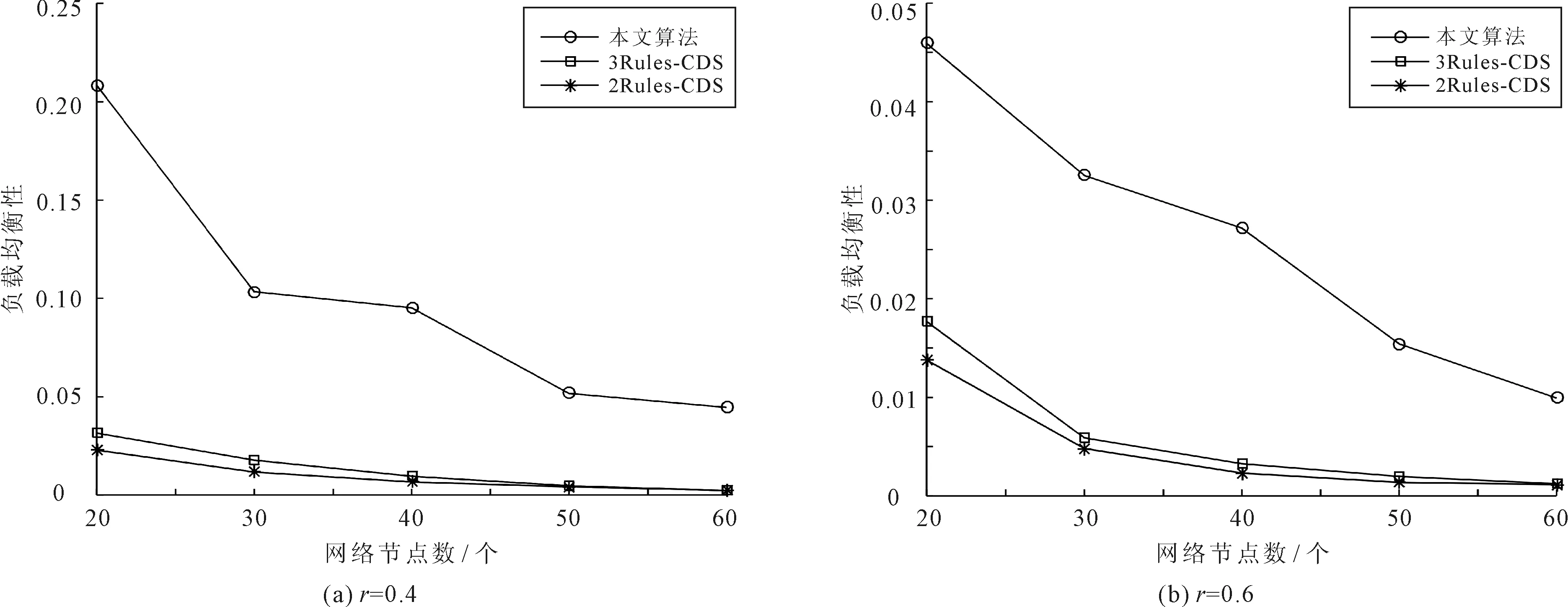
图2 负载均衡性对比

网络中各节点平均剩余能量随网络节点数的变化趋势如图3所示。从中可见，3种算法的各节点平均剩余能量都随着网络节点数的增加呈下降趋势。本文算法的各节点平均剩余能量之所以优于其余两种算法，是因为所给算法考虑了网络负载均衡因子，使得网络中支配节点和支配邻居节点分布更均衡，提高了网络的负载均衡性，从而节省了网络节点的能量消耗，进而延长了网络生命周期。

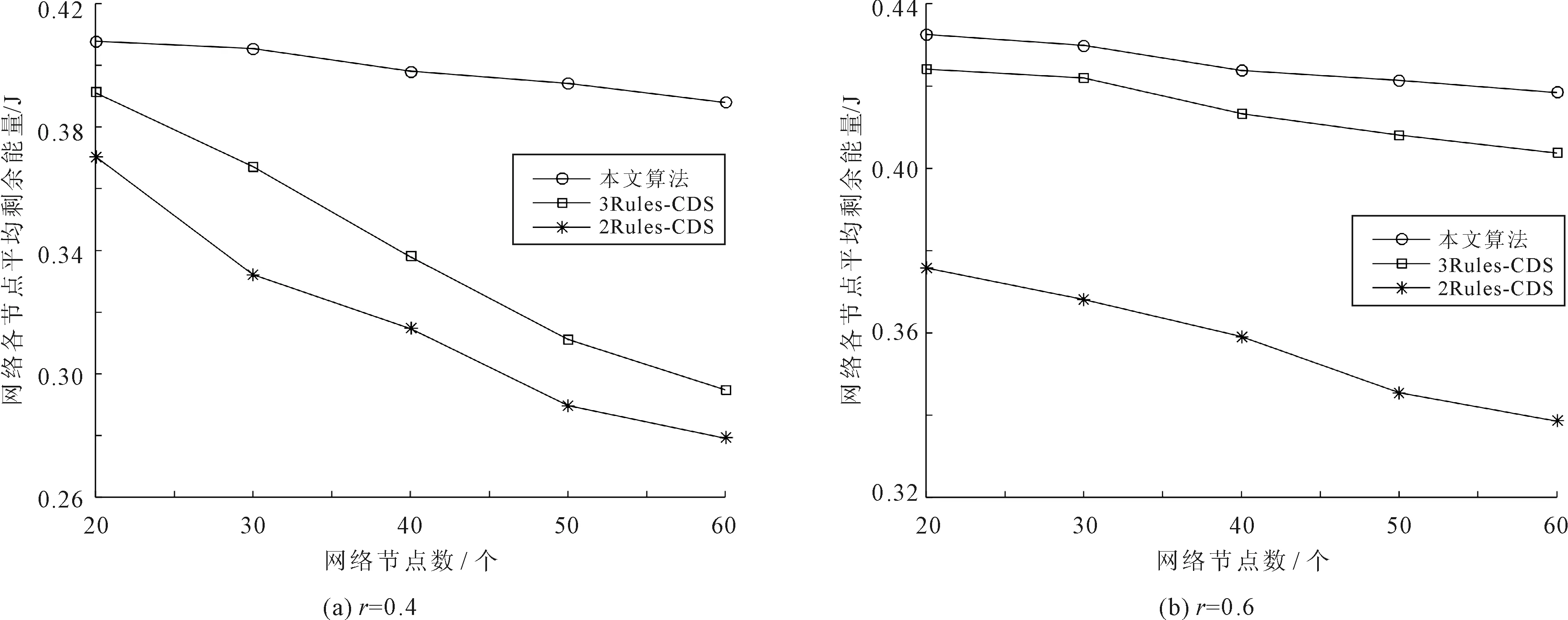
图3 网络剩余能量对比

4 结语

考虑网络的度中心性、特征矢量中心性和紧密中心性这3个网络影响因素,作为选取支配节点的标准，并引入连通维护策略保障网络中支配集的连通性，构建一种新的分布式连通支配集生成算法。所给算法综合考虑节点在网络中的局部、全局和物理位置方面对网络负载均衡的影响因素，可有效改善利用最小连通支配集算法所建网络拓扑并非具有良好负载均衡性的问题。与2Rules-CDS算法和3Rules-CDS算法相比，本文所给算法使整个网络中支配节点和被支配节点分布更加均匀，明显改善了网络负载均衡性，进而延长了虚拟骨干网寿命。