基于集对分析-可变模糊集耦合方法的溃坝环境影响评价
2019-01-21李宗坤徐宏殷
李宗坤,李 巍,葛 巍,徐宏殷
基于集对分析-可变模糊集耦合方法的溃坝环境影响评价
李宗坤1,李 巍1,葛 巍1,徐宏殷2
(1. 郑州大学水利与环境学院,郑州 450001;2. 天津大学建筑工程学院,天津 300350)
针对溃坝环境影响研究内容存在复杂性和不确定性的问题,综合考虑植被覆盖、河道形态、生物多样性、人居景观环境、污染工业、水环境、土壤环境等溃坝环境影响因素,构建并细化了溃坝环境影响评价指标体系和评价等级标准.以集对分析理论核心概念“联系度”和可变模糊集理论核心概念“差异度”在本质上相同为纽带,将改进细化的集对分析联系度函数与可变模糊集理论相结合,用联系度的概念来简化差异度的计算公式,将得到的特征函数代替可变模糊集中的相对差异度函数.建立溃坝环境影响的集对分析-可变模糊集耦合评价模型,实现了集对分析理论与可变模糊集理论的优势互补.将溃坝环境影响的集对分析-可变模糊集耦合评价模型应用于沙河集水库大坝,结果表明:本文模型的评价结果客观合理,更加全面地反映了溃坝环境影响系统的非线性和可变模糊性,符合溃坝环境影响系统的模糊不确定性特点,同时简化了可变模糊差异度的构建过程,提高了评价效率,为溃坝环境影响评价提供了一种科学的方法.
溃坝;环境影响;风险后果;集对分析;可变模糊集
溃坝环境影响风险评价由于涉及到的内容多,影响因素具有多样性、不确定性和可变性等原因,相比于其他溃坝风险后果的研究成果较少[1].随着社会、经济的不断发展,研究溃坝环境影响不仅有利于帮助决策者全面认识大坝的风险水平,做出更科学的风险决策,而且对于完善溃坝风险后果评价体系及大坝风险管理理论都具有重要的意义[2].在溃坝环境影响的量化研究中,目前评价方法主要有模糊数学评价 法[3]、能值足迹法、综合社会环境影响指数评价法[4]、层次分析法[5]以及下游数字模拟法[6]等.以上方法在对溃坝环境影响评价做出探索的过程中,存在对数据要求过高、评价等级差异不明显以及主观性较强的问题,本文采用较为全面客观反映事物不确定性的可变模糊集理论对溃坝环境影响进行评价研究.
1 溃坝环境影响评价指标体系及等级标准
1.1 指标体系
构建溃坝环境影响评价模型的基础和前提是溃坝环境影响评价指标体系.由于溃坝环境影响的定义多种多样[4-7],目前还没有统一的定义,其实质是指周边区域的生态环境条件和自然环境条件在受到水库溃坝影响后发生的变化,其中自然环境条件影响的评价内容主要是水、大气、噪声、固体废物等要素;生态环境条件影响在直观上则体现在“水土”和“生物”两个方面.本文根据溃坝行为特点,结合《中华人民共和国环境保护法》、《中华人民共和国环境影响评价法》、《水利水电工程环境影响评价导则》等相关法律法规,依据评价指标筛选的系统性、典型性及定性与定量相结合等原则,在文献[4-5]的研究基础上,确定7个方面作为溃坝环境影响评价指标,7个评价指标分别为河道形态、植被覆盖、生物多样性、人居景观环境、污染工业、水环境及土壤环境.
1.2 指标取值标准
文献[4-5]的研究,将溃坝环境影响严重程度分为5个等级,评价语分别为“轻微”、“一般”、“中等”、“严重”和“极其严重”,并根据以上5个评价等级,拟定溃坝环境影响评价指标取值标准.其中“河道形态”为定量指标,通过单位长度单位宽度冲刷或淤积量进行量化,定量指标“植被覆盖”采用土地受损率与严重性进行量化.定性指标采用将0~100按等级划分区间的方法进行专家赋值.本文对定性指标中水环境和土壤环境的赋值进行了改进:前人多采用水质或土壤成分灾后采样分析方法进行确定,但由于溃坝环境影响风险评价是在假设溃坝情况下的一种风险预测,无法对溃坝后水质和土壤质量评价等级的变化进行确定,且水环境和土壤环境的影响也无法进行模拟,较难获得直接的数据资料,因此,本文结合《地表水环境质量标准》和《土壤环境质量标准》,以定性指标评价标准赋值区间为基础,根据现有水土环境的敏感度划分其等级.例如,大坝下游原水环境或土壤环境质量标准越高,则其对溃坝洪水影响的敏感度越高,相应的风险等级越高.评价指标对应各等级取值标准如表1所示.
表1 溃坝环境影响评价指标取值标准

Tab.1 Environmental impact assessment index of dam breach
2 集对分析-可变模糊集耦合评价模型
2.1 集对分析理论
集对分析(set pair analysis)是一种处理由随机、模糊、中介和信息不完全所导致事物不确定性的系统理论方法,由我国学者赵克勤[8]于2000年首次提出,已在风险分析、水资源预测、信息系统等诸多领域得到了广泛应用[9-14].针对要研究的问题,建立集对=(,),其中和是具有一定联系的两个集合,两集合在同、异、反3方面的特性可以通过联系度进行定量刻画,其中联系度的表达式为

(1)
式中:为同、异、反联系度;、、分别为集合和的同一度、差异度和对立度,,,∈[0,1],且++=1;为集合的总特性数;、分别为两集合的同一特性数和对立特性数;;为差异度系数;为对立度系数.联系度是集对分析理论的基石,通过其可描述随机、模糊、灰色等常见的不确定现象[11].
2.2 可变模糊集理论


(2)
设为相对隶属度等于1的点,为区间内任意点的量值,则落入点左侧时的相对差异函数模型为
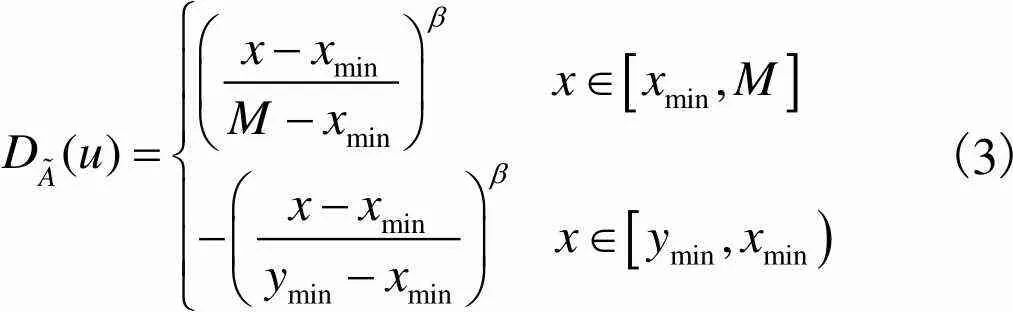
(3)
落入点右侧时的相对差异函数模型为

(4)
式中:max、min分别为指标评价区间的上、下限值;max、m分别为可变范围评价区间上、下限值;为非负指数,一般取=1.
的选取是计算相对差异度的难点,需要根据物理意义或专家定义来进行赋值,在处理定量概念时较好对待,通常取物理中值,但是对于定性概念的处理就要求专家有较好的赋值经验及水平,否则将直接造成计算结果的偏差.
2.3 集对分析-可变模糊集耦合评价模型
水库溃坝环境影响系统具有不确定和不完备的特点,作为处理不确定性问题的系统理论方法,集对分析与可变模糊集理论对其均具有适用性的同时兼有各自的特点和不足.两种理论的核心参数分别是“联系度”和“差异度”.在传统集对分析联系度构造的过程中,简单地将评价样本落入相隔或相邻等级的联系度进行确定性简化,导致评语不够细化,不符合现实事物的不确定性特点,且在利用最大集对势原理进行等级判断时存在信息丢失的问题;可变模糊集理论更能准确反映事物的模糊性,但其核心参数相对差异度的确定过程依赖经验且不易于刻画定性指标[20-21].当采用可变模糊集理论评价环境影响时,指标体系中大量定性概念的点值确定较为困难,根据可变模糊相对差异度来自于“吸引减排斥”的本质内涵,本文通过构建改进的集对分析联系度来反映可变模糊差异度.前人的探索中只保留了集对分析中“同”的信息,相当于只考虑了可变模糊概念中的“吸引”,而对承载“差异”和“排斥”部分的信息全部忽略,存在大量信息丢失,显然是不全面的.本文建立的集对分析-可变模糊集耦合评价模型,以“联系度”和“差异度”概念的相似本质为纽带,将两种评价方法有机结合,用深层次刻画改进后的集对分析联系度来代替可变模糊差异度的确定过程.在等级判断时,利用可变模糊集理论中可变参数组合,确定各参数组合下的综合隶属度向量,并计算对应的等级特征值,通过分析等级特征值的稳定性,最终确定待评价水库的环境影响风险等级.具体计算步骤如下.
(1) 构建指标评价值与取值标准集合.设集合=(1,2,…,q)与集合分别表示各指标评价值集合与取值标准集合,构建集对=(,),其中
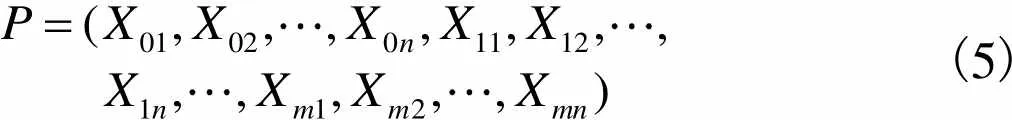
(5)
(2) 确定集对联系度-相对差异度.针对传统集对分析方法构建联系度过程中没有考虑评语细化的问题[18],本文利用联系度可拓展性对联系度表达式进行改进,将异、反进一步细分为优异、劣异和优反、劣反,将式(1)进行细分改进得
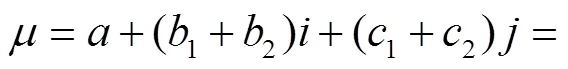

(6)
式中:+1+2+1+2=1;+∈[0,1];-∈[-1,0];+={0,1};-=-1.
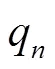

(7)

(8) (9) (10) (11)
式中:q指第项评价指标的评价值;0n、1n、2n、3n、4n、5n分别为第项评价指标对应各取值标准界限值.
根据上述计算可知,μ越接近1,则表示评价对象与所讨论评价等级间的一致性越大,样本越趋于该评价等级,反之亦然.因此,上述计算的单指标联系度可作为可变模糊集中的相对差异度使用.
(3) 确定相对隶属度.应用上述构建的可变模糊相对差异度,计算评价对象隶属于模糊评价等级的相对隶属度,即

(12)
(4) 确定指标权重.本文指标权重值参考文献[5]中的层次分析法计算结果.
(5) 计算综合隶属度.溃坝环境影响等级对风险级别的综合相对隶属度为

(13)
式中:为指标权重;为优化准则参数,=1为最小一乘方准则,=2为最小二乘方准则;为距离参数,=1为海明距离,=2为欧氏距离.和统称为可变模型参数,通常有4种组合:①=1,=1;②=1,=2;③=2,=1;④=2,=2.
(6) 确定级别特征值及评价等级.4种参数组合下可变模糊识别模型之间的联系,是可变模糊识别方法的一个重要特点.通过采用式(13)中模型参数、的4种不同组合,可计算得到4组综合隶属度向量,对其进行归一化处理可得到满足归一化要求的综合隶属度向量.5个评价等级用数字1~5对应,根据式(14)和式(15)计算水库溃坝环境影响级别特征值,得到4种模型参数下待评价水库的溃坝环境影响等级变动范围,分析级别特征值的稳定性,最终确定待评价水库的溃坝环境影响风险等级.

(14)

(15)
3 实例应用
3.1 工程概况
本文以安徽省滁州市沙河集水库为例进行模型应用,沙河集水库于1979年基本建成,总库容1.85×108m3,下游保护人口30多万,农田20多万m2.该水库大坝于1999年被鉴定为三类坝,2000年5月开始除险加固,2002年12月加固完成.
3.2 沙河集水库溃坝环境影响评价
为便于对比分析,本文采用文献[3]的指标数据作为原始数据.考虑到专家赋值的人为因素影响,本文采用平均值法对文献[3]的指标数据进行复核,认为其赋值基本合理,可以作为本文的评价依据.各项评价指标的评价值如表2所示.
表2 沙河集水库溃坝环境影响评价指标评分

Tab.2 Environmental impact assessment index score of dam breach in Shaheji reservoir
利用式(7)~式(12)计算沙河集水库溃坝环境影响指标对各评价等级的相对隶属度,本文、的取值根据集对分析理论中差异度系数和对立度系数的均分原则,参考系数特殊取值法,选取+=0.5,-=-0.5,+=0,-=-1.计算结果如表3所示.
利用式(13)~式(15)计算沙河集水库溃坝环境影响在不同可变模糊集模型参数下的归一化综合隶属度向量,以及对应模型的级别特征值,计算结果如表4所示.
由表4中的计算结果可知,在4种不同模型参数组合下的综合隶属度向量计算结果中,各级别隶属度分布趋势一致且稳定性较好.根据不同模型参数下的级别特征值计算结果可知,沙河集水库溃坝环境影响的级别特征值=3.42,属于1~5级中的[3,4]区间,故评价等级应为第4级,即沙河集水库溃坝环境影响风险程度为“严重”.
表3 沙河集水库溃坝环境影响评价指标相对隶属度计算结果

Tab.3 Calculation results of the relative membership degree of environmental impact assessment index of dam breach in Sha-heji reservoir
表4 归一化综合隶属度向量及级别特征值计算结果

Tab.4 Normalized comprehensive membership vector and level eigenvalue calculation results
3.3 结果对比分析
将上述评价结果与其他方法的评价结果进行对比,如表5所示.
表5 沙河集水库溃坝环境影响不同评价方法的评价结果对比

Tab.5 Comparison of evaluation results of environmental impact of dam breach in Shaheji reservoir
从表5的评价结果对比中可以看出:
(1)本文模型的评价结果与其他已有评价方法的评价结果基本一致,表明溃坝环境影响集对分析-可变模糊集耦合评价模型合理可行;
(2)常规集对分析方法未明确给出差异度和对立度系数、的值,只是将其看作特征符号,且利用最大集对势来确定最终评价等级,只考虑了两集合“同”和“反”的关系,未考虑差异关系,均导致部分信息丢失,对问题的整体性描述较弱.与常规集对分析相比,本文的评价模型运用集对联系度的可展性对联系度计算公式进行细分改进,、被赋予具体数值保证了评价信息的完整性,以此构建可变模糊相对差异度函数,更加全面客观地考虑了事物的不确定性本质,简化了可变模糊差异度的构建过程.在综合隶属度计算中,全面地反映了事物的非线性和可变模糊性,更加符合溃坝环境影响系统的模糊不确定性特点;
(3)可变模糊集理论考虑4种不同的可变模型参数,更好地反映了模糊概念的相对性和动态可变性,避免了模糊集合理论中隶属函数存在静态化的问题,并且较好地解决了模糊数学等方法不易区分相邻两类差异、难以反映评价过程中不确定性以及评价指标不兼容等问题.
本文所采用模型的评价结果与综合影响系数法以及模糊数学理论评价方法的评价结果相差一个等级,主要原因是:综合影响系数法将溃坝社会影响和环境影响合二为一,并且评价结果是结合了溃坝概率后的综合结果,并非是针对溃坝环境影响单项的评价;同时文献[4]提到,沙河集水库“由于其为支流上的中型水库,环境影响系数普遍较低”,可见是由于下游较多的风险人口和较高的溃坝概率才得出了“不可容忍”的评价结果;模糊数学理论评价法的评价准则是最大隶属度原则,从表4可以看出,如果运用最大隶属度原则进行评价,本文4种模型参数下的评价结果也均为“极其严重”等级.当某两个等级的隶属度非常相近时,如本文中4种模型参数计算结果中“极其严重”和“严重”两个等级间的差异仅为1%~7%,若采用最大隶属度原则进行等级判断,可能存在判断失真的问题.因此,本文模型运用级别特征值作为最终等级判断的依据更加客观、准确.
4 结 语
溃坝是一种具有不确定性的低概率高损失风险事件,本文根据风险因子指标对溃坝事件的风险敏感性以及风险承受能力的强弱,进一步细化完善了溃坝环境影响评价指标取值标准.综合集对分析理论和可变模糊集理论两种处理不确定性问题的系统理论方法,改进了集对分析法的联系度刻画公式,并运用其构造可变模糊集的相对差异度函数,建立了溃坝环境影响的集对分析-可变模糊集耦合评价模型,将该模型应用于沙河集水库大坝,实例应用与结果对比分析表明,本文模型应用于溃坝环境影响评价合理可行,且结果更为客观全面,为溃坝环境影响评价提供了一种科学的方法.
[1] 李宗坤,葛 巍,王 娟,等. 中国水库大坝风险标准与应用研究[J]. 水利学报,2015,46(5):567-573.
Li Zongkun,Ge Wei,Wang Juan,et al. Risk criteria and application on reservoir dams in China[J]. Journal of Hydraulic Engineering,2015,46(5):567-573(in Chinese).
[2] 李宗坤,葛 巍,王 娟,等. 中国大坝安全管理与风险管理的战略思考[J]. 水科学进展,2015,26(4):589-595. Li Zongkun,Ge Wei,Wang Juan,et al. Strategic consideration of dam safety management and risk management in China[J]. Advances in Water Science,2015,26(4):589-595(in Chinese).
[3] 程 莉,周 晶. 基于模糊数学理论的溃坝环境影响分析[J]. 价值工程,2013(15):290-292.
Cheng Li,Zhou Jing. Environmental impact analysis of dam failure based on fuzzy mathematical theory[J]. Value Engineering,2013(15):290-292(in Chinese).
[4] 王仁钟,李 雷,盛金保. 水库大坝的社会与环境风险标准研究[J]. 安全与环境学报,2006,6(1):8-11. Wang Renzhong,Li Lei,Sheng Jinbao. On criterion of social and environment risk of reservoir dams[J]. Journal of Safety and Environment,2006,6(1):8-11(in Chinese).
[5] 何晓燕,孙丹丹,黄金池. 大坝溃决社会及环境影响评价[J]. 岩土工程学报,2008,30(11):1752-1757. He Xiaoyan,Sun Dandan,Huang Jinchi. Assessment on social and environment impacts of dam break[J]. Chinese Journal of Geotechnical Engineering,2008,30(11):1752-1757(in Chinese).
[6] Seker D Z,Kabdasli S,Rudvan B. Risk assessment of a dam-break using GIS technology[J]. Water Science & Technology,2003,48(10):89-95.
[7] Lindell M K,Prater C S. Assessing community impacts of natural disasters[J]. Natural Hazards Review,2013,4(4):176-185.
[8] 赵克勤. 集对分析及其初步应用[M]. 杭州:浙江科学技术出版社,2000.
Zhao Keqin. Set Pair Analysis and Its Preliminary Application[M]. Hangzhou:Zhejiang Science and Technology Press,2000(in Chinese).
[9] Wang Wensheng,Jin Juliang,Ding Jin,et al. A new approach to water resources system assessment:Set pair analysis method[J]. Sci China Ser E-Tech Sci,2009,52(10):3017-3023.
[10] Wu F F,Wang X. Eutrophication evaluation based on set pair analysis of Baiyangdian lake,North China[J]. Procedia Environmental Sciences,2012,13(3):1030-1036.
[11] 孟宪萌,胡和平. 基于熵权的集对分析模型在水质综合评价中的应用[J]. 水利学报,2009,40(3):257-262.
Meng Xianmeng,Hu Heping. Application of set pair analysis model based on entropy weight to comprehensive evaluation of water quality[J]. Journal of Hydraulic Engineering,2009,40(3):257-262(in Chinese).
[12] Liu Y. Study on environment evaluation and protection based on set pair analysis——A case study of chongqing[J]. Energy Procedia,2012,14(14):14-19.
[13] 钟登华,杨士瑞,张琴娅,等. 基于改进集对分析方法的高心墙堆石坝填筑工期仿真及风险评价[J]. 水力发电学报,2015,34(3):137-144.
Zhong Denghua,Yang Shirui,Zhang Qinya,et al. Filling construction period simulation and risk assessment of high core rock-fill dam based on improved set pair analysis method[J]. Journal of Hydroelectric Engineering,2015,34(3):137-144(in Chinese).
[14] Yang Fengguang,Liang Yue,Vijau P S,et al. Debris flow hazard assessment using set pair analysis models:Take beichuan county as an example[J]. J Mt Sci,2014,11(4):1015-1022.
[15] 陈守煜. 可变模糊集理论与模型及其应用[M]. 大连:大连理工大学出版社,2009. Chen Shouyu. Variable Fuzzy Sets Theory and Model and Its Application[M]. Dalian:Dalian University of Technology Press,2009(in Chinese).
[16] Chen S Y,Xue Z C,Li M,et al. Variable sets method for urban flood vulnerability assessment[J]. Science China Technological Sciences,2013,56(12):3129-3136.
[17] Zou Qiang,Zhou Jianzhong,Zhou Chao,et al. Comprehensive flood risk assessment based on set pair analysis variable fuzzy sets model and fuzzy AHP[J]. Stochastic Environmental Research and Risk Assessment,2013,27(2):525-546.
[18] 魏明华,郑志宏,黄 强,等. 基于改进SPA法的地下水环境模糊综合评判[J]. 水利学报,2009,40(10):1204-1209.
Wei Minghua,Zheng Zhihong,Huang Qiang,et al. Fuzzy comprehensive evaluation of groundwater environment based on improved set pair analysis[J]. Journal of Hydraulic Engineering,2009,40(10):1204-1209(in Chinese).
[19] Chen S Y,Xue Z C,Li M. Variable sets principle and method for flood classification[J]. Science China Technological Sciences,2013,56(9):2343-2348.
[20] Kumar K,Garg H. TOPSIS method based on the connection number of set pair analysis under interval-valued intuitionistic fuzzy set environment[J]. Comp Appl Math,2016(1):1-11.
[21] Yue Wencong,Cai Yanpeng,Rong Qiangqiang,et al. A hybrid life-cycle and fuzzy-set-pair analyses approach for comprehensively evaluating impacts of industrial wastewater under uncertainty[J]. Journal of Cleaner Production,2014,80:57-68.
(责任编辑:孙立华)
Dam Breach Environmental Impact Evaluation Based on Set Pair Analysis-Variable Fuzzy Set Coupling Model
Li Zongkun1,Li Wei1,Ge Wei1,Xu Hongyin2
(1. School of Water Conservancy and Environment,Zhengzhou University,Zhengzhou 450001,China;2. School of Civil Engineering,Tianjin University,Tianjin 300350,China)
In this study,considering the complexity and uncertainty of dam breach environmental impacts,an evaluation index system and standard of division are constructed considering vegetation cover,channel morphology,biodiversity,human ecological environment,industrial pollution,water environment,and soil environment as the main factors. Considering the concepts of connection degree and difference degree in set pair analysis theory and variable fuzzy set theory,respectively,a new coupling evaluation model is established based on the improved set pair connection degree and variable fuzzy set theory to overcome the inaccuracy defect when variable fuzzy model is used to deal with qualitative index. The coupling model realizes the complementary advantages of set pair analysis theory and variable fuzzy set theory. The model was applied to the Shaheji reservoir dam. Compared to previous studies,the coupling model is reasonable and more objective and it more comprehensively reflects the non-linearity and variable fuzziness of the dam breach environmental impact system. Moreover,the variable ambiguity is in line with the fuzzy uncertainty characteristics of the dam breach environmental impact system;this simplifies the construction process of variable fuzzy difference degree and improves the evaluation efficiency. Therefore,the established model provides a new method for environmental impact assessment of dam breach.
dam breach;environmental impact;risk consequence;set pair analysis;variable fuzzy sets
10.11784/tdxbz201807030
TV641
A
0493-2137(2019)03-0269-08
2018-07-25;
2018-10-15.
李宗坤(1961— ),男,博士,教授,博士生导师,lizongkun@zzu.edu.cn.
葛 巍,gewei@zzu.edu.cn.
国家自然科学基金资助项目(51679222,51709239,51379192);河南省高等学校重点科研项目(18A570007).
the National Natural Science Foundation of China(No.51679222,No.51709239,No.51379192),the Key Research Program of Universities in Henan Province(No.18A570007).
