基于多元回归模型的任务定价问题

李清华,王 旭,朱义九,李浩远

(烟台大学数学与信息科学学院,山东 烟台 264005)

随着网络的快速发展以及人们生活水平的提高,我国出现了一些新兴的产业.“拍照赚钱”自助式服务模式随即产生.这种基于移动互联网的自助式劳务众包平台,为企业提供各种信息搜集和商业检查,与传统的市场调查方式相比,有着显著的优点,所以APP成为该平台的运行核心,而APP中的任务定价又是重中之重.为了避免因为定价不合理而导致任务失败,合理定价是一个亟待解决的问题.本文建立多元回归模型对任务合理定价问题进行研究.

任务定价问题就是对APP上需要拍照的任务进行合理定价,要解决该问题需要研究如何确定影响该任务定价的因素.本文将任务经纬度、附近会员数量、限额总数以及人口密集程度考虑在内,利用最小二乘估计建立多元回归模型,并对任务完成度进行比较,从而解决任务定价问题.

1 多元回归模型

了解到对于不同的任务,人们总是优先考虑距离自己较近的,因此可将任务地理位置按照一定要求进行聚类,得到不同区域的任务情况.本文以文献[1]中的任务定价问题为研究对象,对材料中所给出的数据进行描点作图,“·”代表已完成任务,“×”代表未完成任务,如图1所示.然后将所给任务地理位置按照行政区域中的地级市进行聚类,分别得到广州市、东莞市、佛山市和深圳市4个区域的任务数量,如图2所示.

以深圳市为例进行分析,通过最近一次全国人口普查数据[2]显示深圳常住人口(含户籍人口)1 190.84万,非户籍人口有806.32万,由Zipf定律[3]可以得到人口分布函数

h(r)=cr-q,

(1)

用来表示相应于位序r的人口规模大小,式中c为常数,q为待定参数,r为该地区在深圳市的位序.通过人口普查数据可以得到深圳市所有地区的位序,运用Matlab软件对参数进行拟合,最终得到人口分布函数为

h(r)=1 086·r1.65.

(2)

图1 任务经纬度散点 图2 4个地级市的任务数量Fig.1 Mission latitude and longitude scatter plot Fig.2 The number of tasks in four prefectur-level cities

建立多元回归模型[4]的一般形式为:

w=β0+β1x1+β2x2+…+βpxp.

(3)

令

y=β0+β1x1+β2x2+…+βpxp+ε,

(4)

其中ε为随机误差,且服从于N(0,σ2),将处理过的观测值数据代入可得

yi=β0+β1xi1+β2xi2+…+βpxip+εi,i=1,2,…,N,

(5)

其中εi为第i组观测值数据的随机误差,且相互独立同服从于N(0,σ2).为了方便,引入矩阵记号[5]:

其中X称为模型设计矩阵,是常数矩阵,Y与ε是随机向量,且Y～NN(Xβ,σ2I),ε～NN(0,σ2I)(I为N阶单位矩阵),ε是不可观测的随机误差向量,β是由未知待定回归系数构成的常数向量.

2 回归系数β的最小二乘估计[6]

(6)

写成分量形式

(7)

则

(8)

(9)

将本题4个影响因素任务地点与市中心的距离L、任务地点附近会员总数n、附近任务限额总数m以及人口分布情况h代入模型,整理得

即

(10)

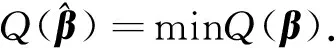
(11)

(12)

通过查阅相关资料[7],可以确定任务定价与任务地点、任务附近会员数量、附近任务限额总数以及人口分布情况的关系如下:

w=a+bL+cn+dm+eh.

(13)

3 模型求解

本研究中深圳市已完成任务数量为35,深圳市任务地点附近会员数量如表 1所示,深圳市任务地点附近任务限额总数如表2所示.

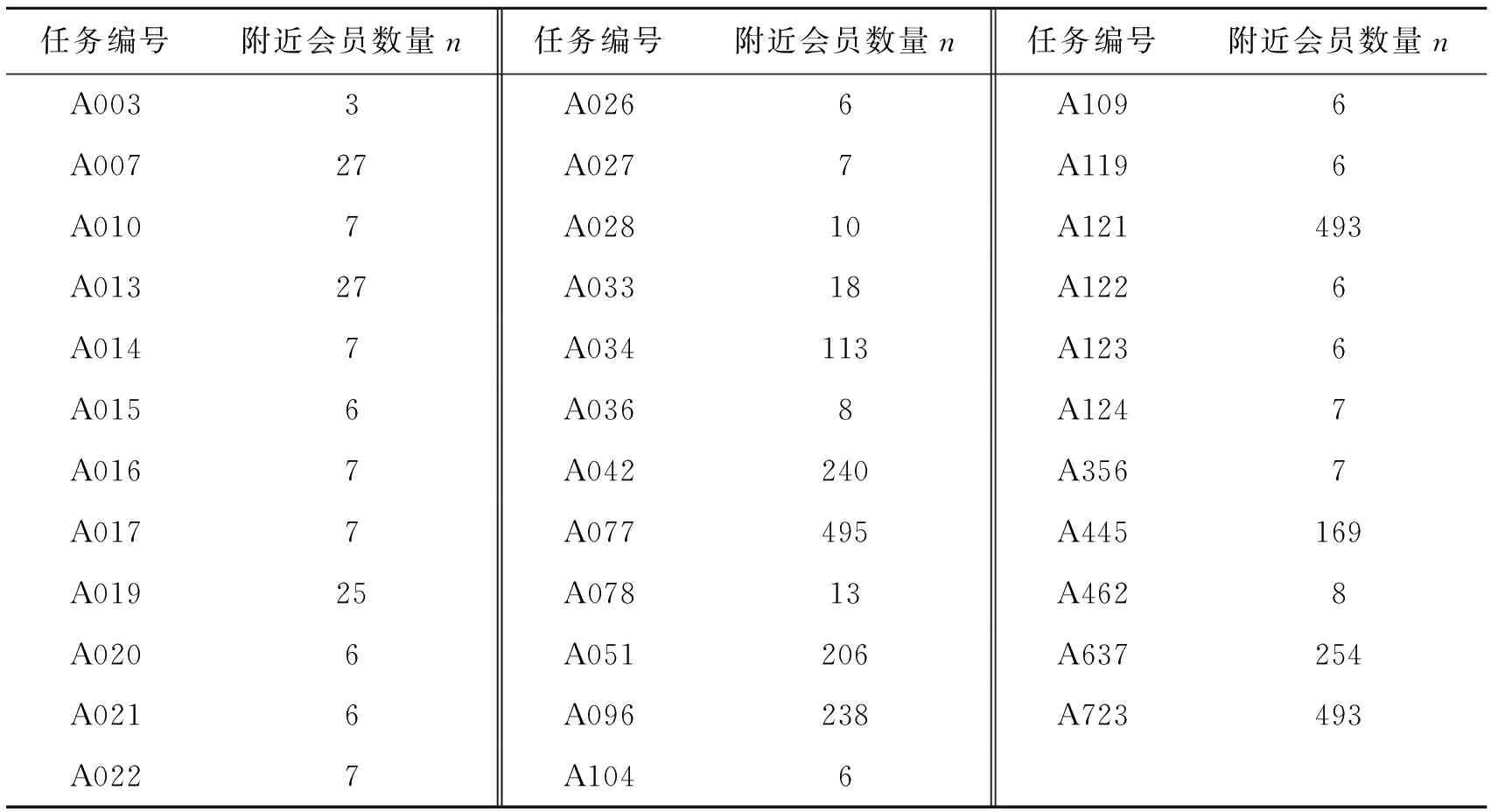
表1 深圳市任务地点附近会员数量Tab.1 The number of members near the mission site in Shenzhen

表2 深圳市任务地点附近任务限额总数Tab.2 Total number of mission quotas near the mission site in Shenzhen

使用Matlab软件进行多元回归拟合可以得到各个参数如下:

a=1.1,b=23.292,c=-1.896,d=-0.26,e=-1.41.

因此,任务定价与自变量之间的关系为:

w=1.1+23.92L-1.896n-0.26m-1.41h.

(14)

通过对数据的预处理可以得出任务总数为589、已完成任务数量为379,任务完成率为64.35%.然后,将任务经纬度、附近会员数量、任务限额总数以及人口密集程度代入模型中,重新得出一组新的任务定价方案,在新定价方案中,任务总数为589、完成数量为492、预测完成率为83.53%.

通过对比可以发现,新的定价方案对任务预测完成率有明显的提高,因此说明模型较为理想.

4 模型显著性检验

定义相关系数[8]

(15)

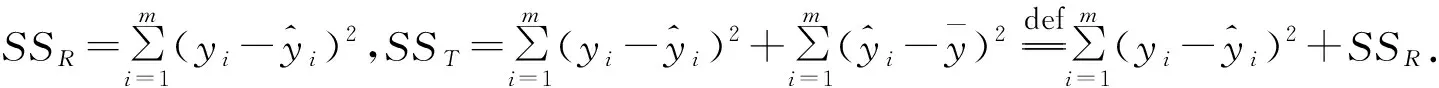
(16)

可以证明:当假设η=β0时,由于yi～N(0,σ2),则

(17)

(18)

取显著性水平α(0.01或0.05),查表得到Fα(m-1,n-m),计算F(m-1,n-m)与Fα(m-1,n-m),做出比较.

通过计算可得U= 2 208 827.94,Q=1 495 164.45.其中,回归平方和U反应任务地点与市中心的距离L、任务地点附近会员总数n、附近任务限额总数m以及人口分布情况h有关.然而残差平方和Q反映的却是除了因素L,n,m,h对任务定价的线性影响,其他的因素对任务定价的影响.因为多元回归方程效果检验是通过检验观测参数和理论参数之间差异的大小,从而确定建立的多元回归模型是否具有实际意义.因此需要将相关的数据代入多元回归方程效果检验的公式中进行参数检验.在实际问题中,一般选择显著水平α=0.01[10].本文的检验结果为

F=4.49>F0.01(3 831)=3.78.

因此确定建立的任务定价多元回归模型的拟合是合理的,是显著的.

模型w中其他所有因素的影响误差为残差平方和SSE减去SSe,记为SSMe,即

因此

即为拟合检验的统计量.

取显著性水平α=0.01,检验结果为

F=0.6

因此说明模型拟合是合理的,是不显著的,即模型的省略项所造成的误差影响可以忽略不计.

5 相较神经网络方法的优势

在任务定价的回归模型中,将求解出的定价数据作为目标值引入神经网络模型.首先,将相关数据代入模型,得出样本点对应的定价方案,并将定价方案作为神经网络模型的训练目标.然后对其进行训练,并对神经网络进行参数的设置.最后运行程序得出结果如下:任务总数为589、完成数量为476、预测完成率为80.81%.由于利用多元回归模型得出任务完成数量为492、预测完成率为83.53%,高于神经网络模型的预测完成率,故多元线性回归模型更为有效.

多元回归模型在分析多种因素时,更加简单和方便.运用多元回归模型,只要采用的模型和数据是相同的,通过标准的统计方法可以计算出唯一的结果.同时多元回归模型可以精确地计量出各个影响因素之间的相关性和回归拟合程度的高低.

但是在多元回归模型中,所选用的因素影响了模型的多样性和某些因素的不可预测性,使得多元回归模型在某些情况下受到限制.

6 结束语

任务定价多元回归方程效果显著,但是同样并不排除其中存在着与任务定价没有线性关系因子的可能性.因此,根据任务定价实际数据进行分析选择因素,是建立合理的任务定价模型的必要条件,显著性检验同样也是模型预测质量的保证.本文以多元回归分析为理论依据,通过构建模型框架推广回归分析的合理应用,使得网上定价更有科学性、可行性以及时效性.不足的是,在对于模型求解时,做了必要的简化假设,在建立任务定价模型时,忽略了任务本身的一些因素,这可能会对模型的精确性产生影响.但是,当任务定价较为合理时,任务本身一些因素不足以对结果产生影响,可以忽略不计.本文建立多元回归模型,利用多方面知识,对任务设计了科学的定价,提高了任务的完成度,具有一定的实际应用价值.