数形结合思想在小学数学教学中的应用

□文/重庆市南岸区天台岗小学校 邹冰秋

《数学课程标准（2011版）》指出：数学是研究数量关系和空间形式的科学。由此可见：数学研究的问题就是数与形这两方面的问题，所以“数”与“形”是数学中最基本的两个研究对象。他们分别是数量关系和空间形式的体现，两者看似对立却又相互统一，在一定的条件下还可相互转化。数与形之间的关系叫做“数形结合”。“数形结合”既是一种重要的数学思想，也是一种重要的数学方法。主要包含了两方面内容：“以形助数”和“以数解形”。利用“数形结合”的思想解决数学问题不仅能使复杂、抽象、枯燥、无味的数学问题变得简单、直观、有趣、生动，而且还助于学生理解题目的含义，有利于学生分析题目中显性和隐性条件的联系，有利于拓宽学生的解题的思路，所以运用“数形结合”的思想解决问题在数学中有着重要的指导意义。那么在现行的小学数学教材中哪些内容体现了“数形结合”思想？“数形结合”思想在教学中有什么作用？笔者认为可从以下几个方面来分析：

一、 数形结合思想，让“粗浅”变“深刻”

小学数学教材中的数学知识呈现方式大多以情景为主，许多学生在阅读教材时被情景吸引，不能对情景背后所蕴含的知识本质进行分析和理解。通过数形结合可以将情景中的数学知识进行提炼，让看似粗浅的问题变为深刻。

例如：在数学人教版教材六年级上册《分数乘分数》时，由于学生在前一节课已经学习了《求一个数的几分之几是多少？》即整数乘分数的含义及方法，学生通过迁移、类推的方法能计算出分数乘分数的结果，但这仅仅只是计算方法的求解，对分数乘分数的含义及为什么要这样计算并没有真正的凸显，所以教材把利用“数形结合”的方式对分数乘分数的含义进行了凸显。

例题为：李伯伯家有一块1/2公顷的地，其中的1/5种土豆，种土豆的面积是多少公顷？根据题意本题也就是1/2公顷的1/5是多少？列式为1/2×1/5=？根据整数乘分数的方法可得：

从上图清晰的表达出：

通过“数形结合”我们可以清晰的知道：求1/2的1/5所表示的含义，通过含义我们理解了算理，有利于加深学生对分数乘分数含义和算理的理解，使原本粗浅的知识变得深刻。

二、数形结合思想，让“模糊”变“清晰”

据研究表明：小学生的思维以具体形象思维为主，特别是小学一、二年级的学生，而且他们的已有认知有限，对于某些抽象的概念认识比较困难，而数学却是以抽象为核心的学科，所以数学教材中的某些知识中对于小学生来说具有一定程度的模糊性和不易理解性。利用“数形结合”的思想和方法能使这些模糊的、难理解的知识转化为清晰、具体的知识，便于学生理解与掌握。

例如，人教版教材在二年级（上册）《认识乘法》一课中，教材出现了如下主题图：

通过分析得出：教材调动了学生已有的知识经验——看图列式，并利用数形结合的思想直观、形象、生动的展示出了情景，引导学生列出加数相同的算式：3+3+3+3+3=15由此让学生初步感知乘法由来。教材运用数与形相结合的方式，降低了学生对知识理解的难度。在实际教学中教师运用多媒体技术连续展现一架小飞机上有三人，然后依次出现这样的第二架飞机，第三架飞机……，一直到第五飞机，提问：一共有多少人呢？学生用同数相加的方法来列式。接着，教师继续出示多架小飞机的画面提问：“如果有6架飞机，10架飞机，甚至100架呢，怎么办？”，学生惊呆了：啊！太多了，太难写了，写不完。”这时，建立乘法的概念水到渠成！教师顺势而导：我们可以用乘法来表示。然后揭示课题“认识乘法”。3+3+3+3+3=15也就是5个3相加，可写成5×3=15，然后用形表示出5、3和15分别表示图中哪些含义。在此数形结合不仅使学生理解了乘法的意义，体会到乘法产生的必要性，而且懂得了乘法就是求几个相同加数的和的简便运算。

由此可见整个数形结合的引导过程。首先，教材利用学生已有的知识经验，利用数形结合的思想和方法使学生体会到“乘法”这个知识点形成过程；其次，教师对教学材料的加工（把5架飞机增加到6架、30架、100架……）使学生充分感悟到在加数相同且数量较多时，列加法算式的不便，促使乘法产生的必要性；最后，学生理解乘法的含义，且通过比较，感悟到乘法的简便。从学生思维活动过程来看，经历了从具体到抽象，一般到特殊的过程。由此证明：在教学中运用数形结合的思想，能够把对学生比较模糊的数学知识变得让学生看得见，摸得着，从而清晰、深刻理解知识的本质，让看似模糊的知识变得清晰。

三、数形结合思想，让“抽象”变“直观”

在教学中，为了激发学生的学习兴趣和让学生感受到数学知识的有用，教师通常以实际生活中的问题进行教学，但通常现实生活中的问题都不易于理解，所以教师常常将生活问题进行数学化，将它们转换成数学问题，再将数学问题转换成用符号或其他图形表示的题目，这样易于理解题意，方便我们解题，并且还能拓宽我们解题的思路。所以教师要培养学生将实际问题转化为数学问题，再将数学问题抽象为图形或符号表达的形式，这样当我们把实际问题数学化，再与形结合起来，很多问题就迎刃而解了。

例如：人教版小学数学教材五年级上册内容（如下图）：

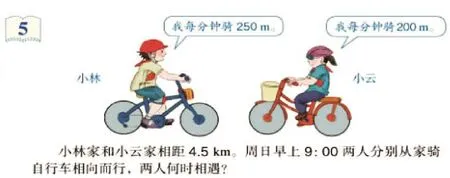
像这样借助直观的线段图把复杂的数学行程问题变得简明、形象，有利于学生对题目含义的理解，能帮助学生能直观地建立“小林走的路程+小云走的路程=4.5千米”这一数量关系，并在此基础上拓宽了学生解决问题的思路。本题通过扬数之长，取形之优，使数量关系与空间形式相得益彰，使抽象的数学问题变得直观、形象，加深了学生对知识的理解从而解决问题。

通过对教材的分析，可以看出数形结合的思想与方法几乎贯穿于整个小学数学教材之中。数形结合通过“以形助数”或“以数解形”，将复杂的问题简单化，抽象的问题具体化，让数学知识由粗浅变得深刻，由模糊变得清晰，由抽象变直观，从而使学生深刻的理解知识的本质，拓宽了学生解决问题的思路。