基于变尺度算法的相控阵波束赋形设计

2019-01-19吴慧峰

舰船电子对抗 2018年6期

吴慧峰

(中国船舶重工集团公司第七二三研究所，江苏扬州 225101)

0 引言

近年来，随着各国武器装备的飞速发展，战场环境变得愈加复杂和恶劣。国内外为了适应恶劣的战场环境，提高军事防御能力和战场生存能力，为了避免雷达探测产生盲区，看不到超低空飞行的目标，采用雷达天线波束赋形技术具有现实意义。

由Selex Galileo公司研制的机场监视雷达是一个大型的X波段圆极化微带天线阵列，其在空间的波束具有余割平方的赋形波束，提高了机场雷达的监视能力，确保了飞行的安全。国产YLC-4远程警戒雷达在仰角上也是采用超余割平方波束来提高高低空的覆盖性能。

常见的波束赋形算法有变尺度算法[1]、Orchard-Elliot方法[2]、基因算法[3]等。变尺度算法的优点是计算速度比较快，在给定不同初值的情况下会得到不同的优化结果，这样可以通过多次计算来得到多组结果[1]。而且程序本身具有全局优化的功能，程序简单明了，操作容易。该优化算法可以实现零点填充、零点形成、副瓣抑制、平顶方向图、余割平方方向图等[1]，本文将对该算法进行研究，为项目中的要求提供技术支持。

1 变尺度优化算法原理

设直线阵列要实现的指定赋形波束F0(θ)，它往往是分贝表示的归一化方向图。直线阵列的阵因子S(θ)要实现指定的赋形波束F0(θ)，这其实是一种对目标方向图的函数逼近。

可建立如下目标函数：

(1)

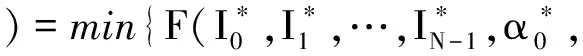
(2)

设置不同的目标函数F0(θ)，经过上述优化算法后就会得到不同的赋形波束。上述优化算法的步骤如下：

(2) 对目标函数F(x)进行求导，计算目标函数的导函数g(x)在xk处的函数值g(xk)作为F(x)在xk点的梯度向量。

(3) 判断‖g(xk)‖是否满足需求，若满足要求，则转第(9)步；若不满足要求，则转第(4)步。

(4) 若对某个整数l，有k=lp，则令：

(3)

并且转第(5)步，否则令：

(4)

其中：

(5)

Δxk-1=xk-xk-1

(6)

Δgk-1=g(xk-xk-1)

(7)

(5) 计算sk=-Hkg(xk)。

(6) 如果〈sk,g(xk)〉≤-er‖sk‖‖g(xk)‖，转第(7)步；否则令Hk=I，转第(5)步；其中er=min[er1,er2‖g(xk)‖]。

(7) 进行一维寻找，求得λk，使得F(xk+λksk)=min[F(xk+λksk)]，λk≥0；x的寻找精度为et=min[et1,et2‖g(xk)‖]，目标函数的精度为et/100。

(8) 令xk+1=xk+λksk。

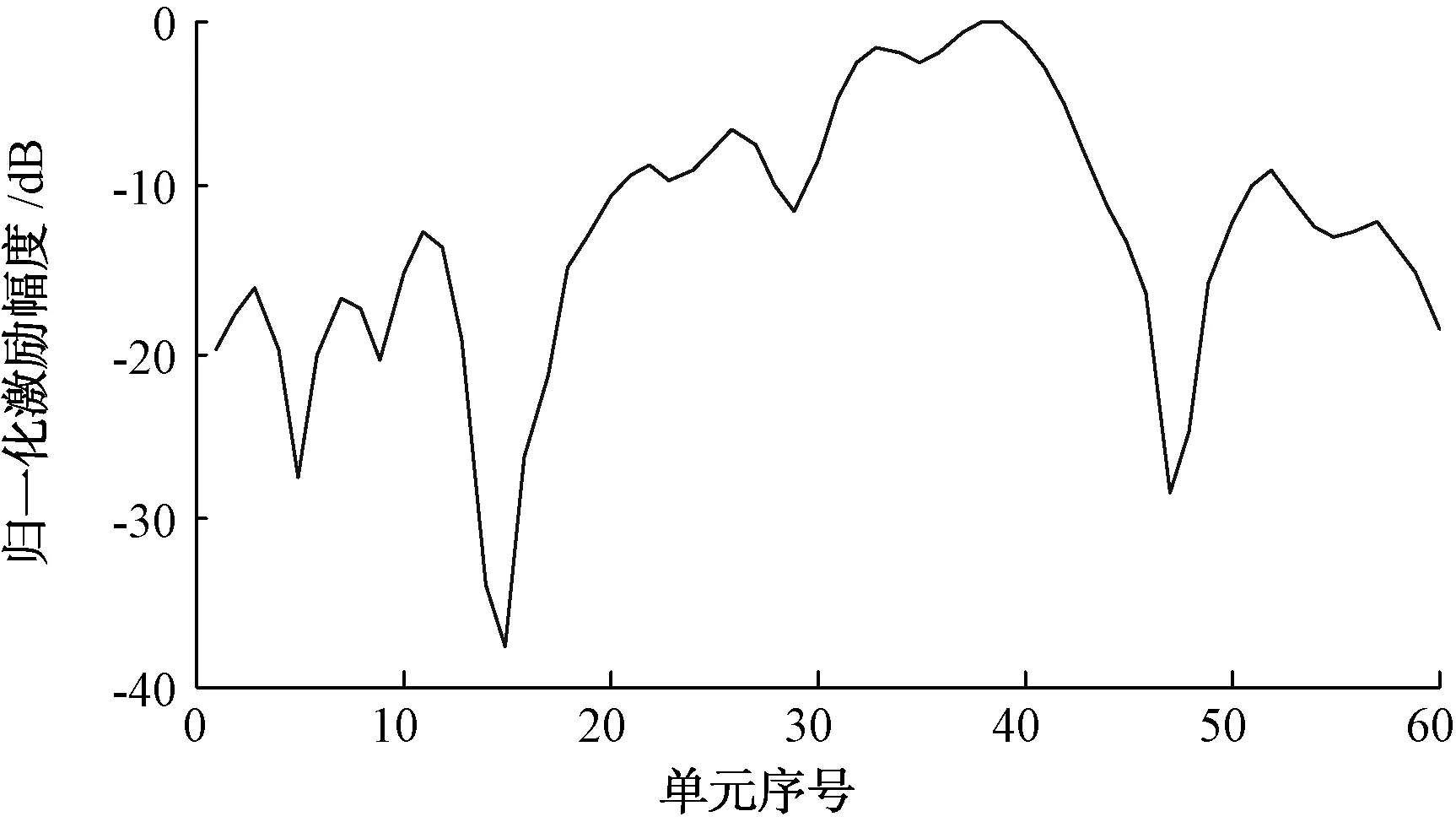
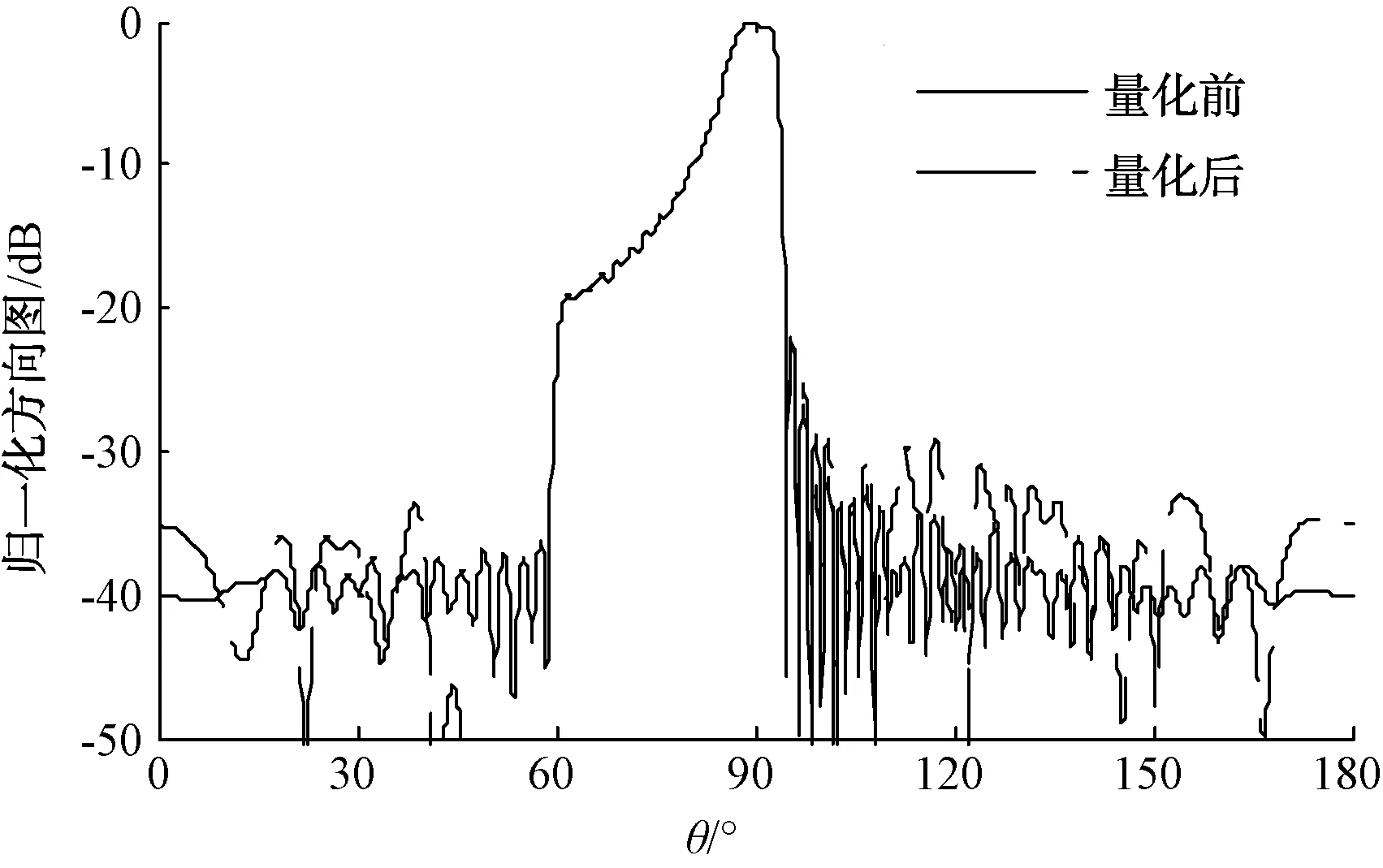
(9) 若F(xk+1)

(10) 若F(xk+1)

(11) 若迭代次数k>lc，停止计算；否则将向量xk+1中每个元素在一定的变化范围内随机改变，并转第(2)步。

上述DFP-BFGS优化算法的步骤中，第(9)到第(11)步为准全局优化搜索。在上述优化算法中需要得到目标函数的模值及目标函数的梯度向量，目标函数中包含线阵的阵因子函数，在对目标函数求导时会用到阵因子函数的模值及导函数，因此接下来推导线阵阵因子及其导函数。

直线阵阵因子为：

(8)

式中：an=Inejαn，un=kxncosθ，θ=0°～180°，k=2π/λ。

线阵阵因子模值为：

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

2 阵列天线波束赋形优化设计实例

假定某相控阵列要在俯仰面实现余割平方波束赋形，其俯仰面具体要求为：工作频段为f0-Δf～f0+Δf，绝对带宽为4 GHz；俯仰单元数为60元；其中心频率的俯仰面波束宽度为8°；其在60°～90°的方向图为csc2(θ)；其他方向的副瓣电平低于-20 dB。

使用这种方向图的天线的地空雷达对于处于同一高度目标的回波信号是相对恒定的。

将上述指标要求转化为目标函数，如图1所示。

图1 方向图目标函数

利用变尺度算法对阵列进行优化设计以逼近上述目标函数，其中各单元间距选为λ0/2，λ0为中心频率波长。将上述优化算法和推导得到的公式利用C语言进行编程优化计算得到各单元的激励幅度与相位，如图2和图3所示。利用上述各单元的激励幅度与相位计算得到的方向图函数与目标函数如图4所示。

图2 各单元激励幅度

图3 各单元激励相位

图4 方向图优化结果

由图4可以得知该优化算法对目标函数的拟合结果良好，满足天线阵列的指标要求。由于相控阵每个阵元的激励幅度相位是由TR组件决定的，现在采用的TR组件都是数字移相器和数字衰减器，其幅度和相位都是阶跃变化的，在此选用0.5 dB阶跃总衰减30 dB的衰减器和6阶数字移相器的TR组件。将上述激励幅度转化为TR能够实现的激励幅度相位分布，如图5和图6所示。根据量化后的激励幅度相位计算得到归一化方向图与量化前的方向图对比结果，如图7所示。