地坐标意义下三维单站无源定位迭代算法

王妙妙，江怡帆，赵 悦，姬利海

(1.北京工业大学,北京 100190；2.北京应用物理与计算数学研究所,北京 100094；3.多伦多大学，多伦多 M5S 2E8；4.东北师范大学,吉林 长春 130024)

0 引 言

无源定位技术能在自身不辐射的条件下,隐蔽确定辐射源位置,具有作用距离远、抗干扰能力强的特点, 对于提高系统在电子战环境下的生存能力和作战效能具有十分重要的作用，因此无源定位已经成为电子对抗的一个相当重要、不可或缺的技术。雷达辐射源无源定位方面现有成果主要针对地面直角坐标系意义下开展的工作[1]。众所周知, 在过去的几十年中，无源定位技术的研究不断深入,主要包括定位精度和效率的分析。其中, 最流行的方法有到达角(AOA),到达时间差(TDOA)和到达频率差(FDOA),可参考文献[2]～ [6]。文献[7]引入了相位差变化率定位算法(定位速度较快, 但相位差变化率测量精度需提高), 但该方法对硬件要求比较高,需要很高的时差测量精度，同时该方法仅适用于大样本定位, 因此对于当前现代相控阵雷达的无源侦察很难有效，对于功率比定位，现有技术功率测量精度很有限。由于空对地侦察过程中受到诸多硬件条件限制, 而基于AOA的单站定位是利用一个平台上单个或多个接收机(绝大部分为单个)在不同时刻对信号方向角测量和处理获得目标方位经纬度信息, 具有经济性、机动性、灵活性, 同时不需要对外数据通信等优点, 所以基于单侦察站(AOA)无源定位是空对地侦察中应用最广的定位方法[8-10]。遗憾的是, 现有算法基本都是基于直角坐标系推导而来, 本文核心算法解决了现有体制采样设备与无源定位算法直接对接问题, 在实际地坐标条件下讨论问题, 同时充分考虑了地球椭球曲率对定位模型的影响。本文给出了实际侦察环境地坐标条件下小样本和大样本无源定位算法, 具体包括三维情形下, 两点定位及理论误差估计算法、大样本广义最小二乘迭代定位算法, 从理论上小样本两点定位确定的解可以作为大样本迭代定位的迭代初值。

下一节给出三维地坐标与地面直角坐标间的转换关系，第2节给出了地坐标条件下小样本定位算法, 该算法可以为后面大样本条件下迭代算法提供基本的迭代公式, 同时可以为迭代算法提供一个比较好的初值, 两点定位误差估计采用等概率曲线来确定误差协方差矩阵所对应的误差椭圆所覆盖的定位概率。直角坐标和地坐标条件下广义最小二乘迭代算法在第3节中给出，数值模拟在第5节中给出, 本节从数值角度分析了第2节中两点交叉定位和第3节中2种迭代定位的定位精度, 同时分析了针对快速移动目标的定位收敛速度、定位精度与目标移动速度之间的依赖关系。第5节给出了总结。

1 三维地坐标与地面直角坐标间的变换

地球的实际形状为椭球, 以地球的球心o1为坐标原点,B点为零度经纬线的交点之一。以o1B所在直线为x1轴的方向, 赤道所在平面上与x1轴垂直的方向为y1轴所在方向,o1z是地心轴所在的直线。赤道接近圆,且半径为r=a=6 378 137 m。y1o1z1所在平面对应的椭圆短半轴为：b=6 356 752 m。

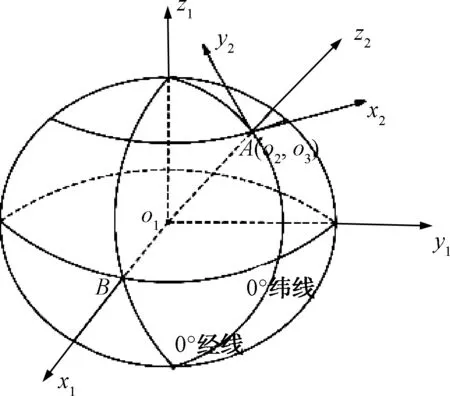
图1 地坐标与地面直角坐标关系示意图

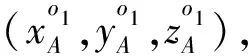
(1)

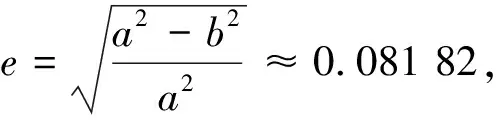
如图1所示,设以A点为坐标圆点的三维直角坐标架为x2y2z2o2(o2与A重合),其中o2y2为过A点的正北方向,o2x2为过A点的正东方向,o2z2过A点铅直于地面。结合公式(1),若仅考虑直角坐标系x1y1z1o1与x2y2z2o2之间的平移关系, 则：

(2)

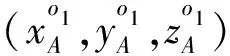
本文中其它地方也用类似的表示方法。另外,显而易见,两坐标架之间还存在着依赖于α,γ的旋转变换,结合公式(2)与旋转变换,一般地,直角坐标系x1y1z1o1与x2y2z2o2之间的坐标变换关系为：

(3)

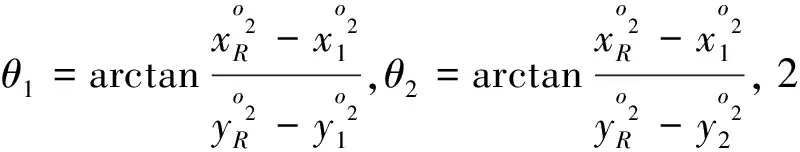
(4)

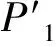
2 三维地坐标小样本定位算法

设两侦察点位P1(α1,γ1,h1),P2(α2,γ2,h2)及其相应的2个点位的侦察目标到达方位角和俯仰角为(θ1,β1),(θ2,β2),基于这些已知条件求侦察目标的经纬度(αR,γR,hR)。三维地坐标小样本定位算法基于直角坐标系下的交叉定位算法,因此需借助上一节中的坐标变换，先把经纬度坐标变换为直角坐标下的形式。由式(1)知,P1(α1,γ1,h1)在x1y1z1o1坐标架中的坐标为:

(5)

(6)

类似地,P2(α2,γ2,h2)在x1y1z1o1坐标架中的坐标为：

(7)

(8)

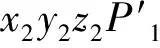
(9)

(10)

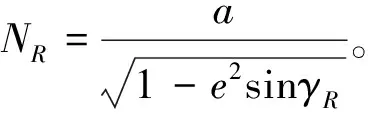
由公式(9)～(10)可知：

(11)

(12)

在直角坐标系下三维交叉定位模型为:

(13)

由公式(6)～(8),(11)～(13)可联立进行两点交叉定位计算(只需用公式(13)中的3个表达式,这时不失一般性, 假设用前3个表达式来交叉定位)。

3 三维地坐标大样本定位算法

接下来讨论三维地坐标条件下广义最小二乘迭代定位算法：

(14)

(15)

根据公式(14),有：

(16)

从式(12)可得到：

(17)

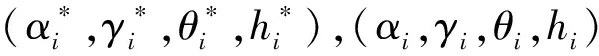
(18)

因此,公式(16)和(17)变成：

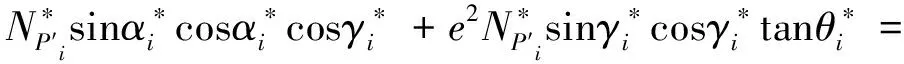
(19)

hR)cosαRcosγR-

(20)

(21)

经一阶泰勒展开，上式可简化为：

(22)

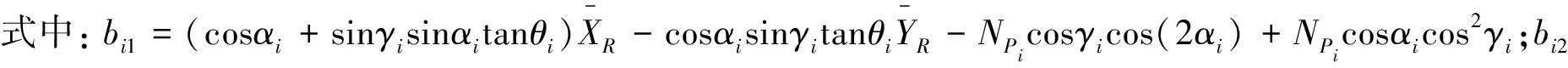
(23)

经一阶泰勒展开，上式可简化为：

-NPicosθicos2γi-(1-

2e2)NPitanβicosγisinγi+

(NR+hR)(1-e2)sinγRtanβicosγi-

(24)

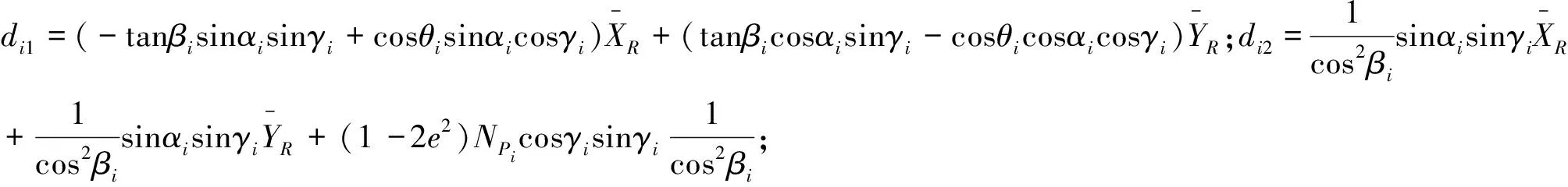
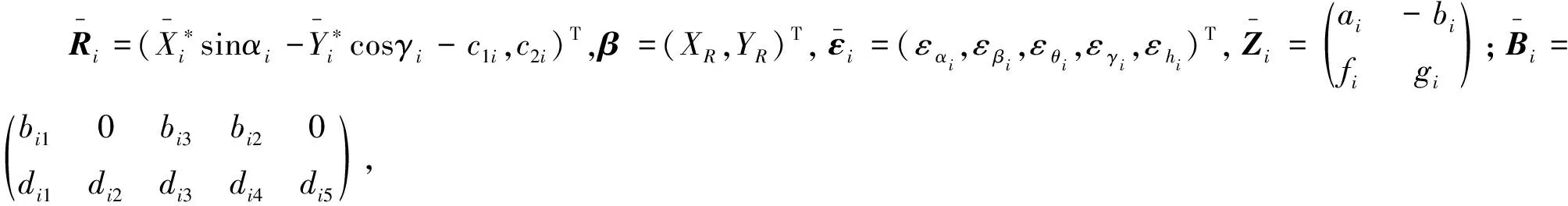
(25)

若样本量m较大时, 可通过下面推广形式的最小二乘估计, 满足公式(21)的待估参数使得采样点拟合残差最小:

(26)

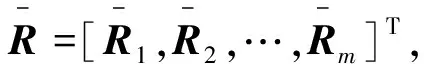
(27)

结合传统的最小二乘估计表达式可给出下面的迭代估计算法：

(4) 循环迭代至收敛。

4 数值模拟

例1(静态侦察目标情形)，设侦察机飞行速度为(300,200)km/h, 初始坐标为(28.5°E,37.3°N),初始到达角为θ=π/3,侦察机初始高度为h=8 km。设每隔dt=0.01 s采集1组数据, 数据量为200, 共采集时间长度为T=1 s。并设采集到样本的误差服从N(0,0.12)的正态分布。假设最小二乘方法初始迭代步数为200, 迭代初值选取为(28.5°E,37.3°N,0.8 km), 迭代收敛误差限制为10-6，则不同目标位置所需要的迭代步数、迭代结果以及相对误差如表1～表3所示。

在以下的数值实验中,定义相对误差如下:

(28)

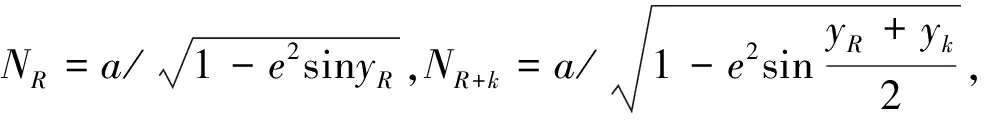
(29)

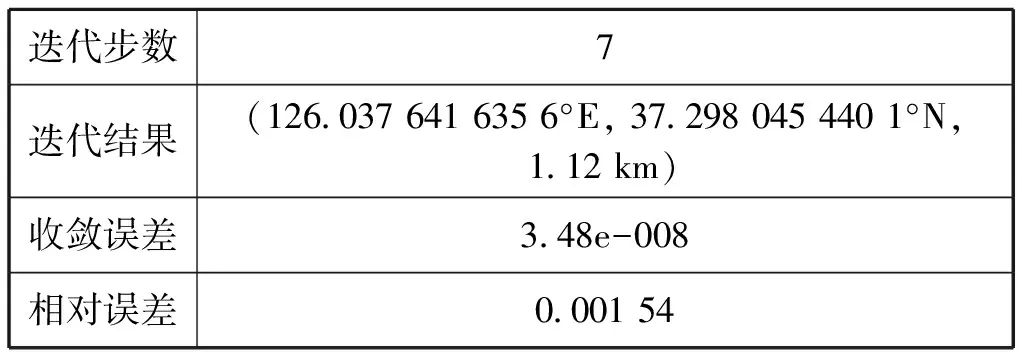
表1 目标位置为(126°E,37°N,1 km)的估计结果

表2 目标位置为(130.49°E,30.38°N,0.5 km)的估计结果

另外, 我们选取2种不同的迭代初值, 定位同一个目标(30°E, 40°N, 1 km)，定位收敛速度、定位精度如表4和表5所示。

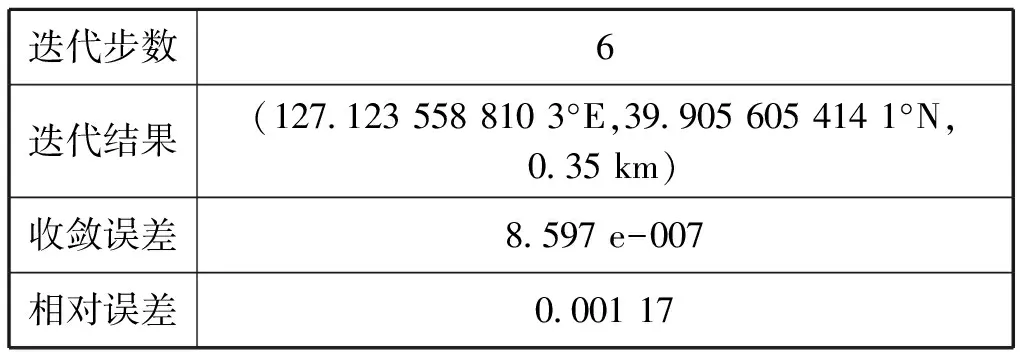
表3 目标位置为(127°E,40°N,0.3 km)的估计结果

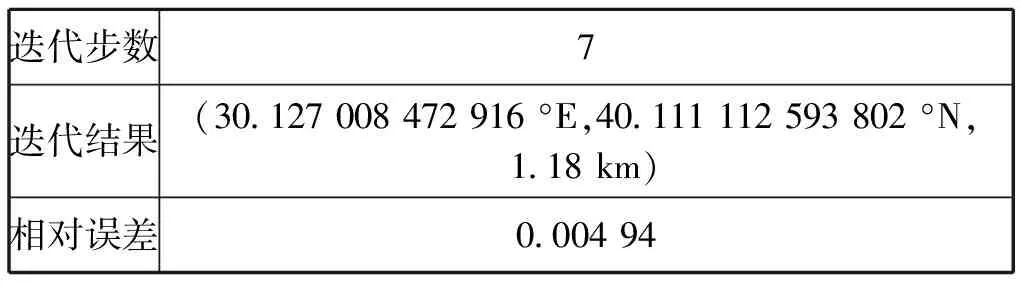
表4 初值为(20°E,30.30°N,0.8 km)的估计结果

表5 初值为(10°E,60°N,4 km)的估计结果

同时, 我们仍然选择同一个定位目标(30°E, 40°N, 1 km), 选择的初值分别为小样本交叉定位坐标与任意坐标, 从定位结果表5和表6可以看到, 利用小样本交叉定位的解作为迭代算法的初值收敛速度更快, 迭代所需要的样本更少, 因此在针对现代相控阵雷达的无源定位侦察过程中很有必要引入该迭代定位思路。

从表4～表6结果可以发现, 本文提出的广义最小二乘算法对迭代初值的依赖不强, 在另一个层面上表明本文所提算法具有很好的稳定性。

表6 初值选取为到达角(AOA)计算得到的值

例 2(动态情形)，假设侦察机的初始参数设置和例1中一样, 不失一般性，假设目标初始位置坐标为(30°E,40°N,1 km), 并设其匀速直线运动速度为VR，则在不同移动速度、不同时刻、相同的迭代初值(20°E,30°N,0.8 km)情况下, 利用最小二乘方法计算结果如表7～表10所示。

表7 速度VR=30 km/h的估计结果

表8 速度VR=45 km/h的估计结果

表9 速度VR=72 km/h的估计结果

表10 速度VR=100 km/h的估计结果

从表7～表10的数值模拟结果可以看出。本文算法对地面移动目标的定位性能。算法的定位收敛速度很快, 收敛误差及相对误差都比较小，定位精度很高, 由此可见本文算法可以成功应用于实际应用中。

5 结束语

本文算法主要应用于对静态目标或慢速移动目标的定位,并且能够达到较高的定位精度。对于移动目标定位可以从数值分析得到满足不同精度需求时本文算法能定位的目标速度的大小, 基本可以满足实际应用中对静态目标和地面快速移动目标的定位需求。缺点是计算太复杂, 影响计算速度，硬件化不太方便等,以后可进一步通过大量例子进行模拟和改进。