一种多机器人分布式编队策略与实现
2019-01-19户晓玲王健安
户晓玲,王健安
(太原科技大学 华科学院,山西 太原 030024)
0 引 言
自20世纪90年代开始,多机器人编队问题一直被众多机器人爱好者广泛研究。E. Bahceci等[1]在2003年将多机器人编队问题定义为:一群机器人通过相互之间的协调,形成并保持一种特定几何形状的队形。多机器人编队控制[2-5]是指多个机器人组成的群体在适应环境约束的条件下保持特定的队形搜索到指定目标的一门控制技术。多机器人编队在执行如目标搜索、地图探测以及地震搜救等复杂任务中,编成特定队形展开目标搜索十分重要。因此,如何让机器人根据指定的搜索目标控制编队迅速形成指定队形具有重要的研究意义。
对多机器人编队控制的研究最早有Reynolds提出的基于行为的编队控制模型[6]、J. P. Desai等提出的领航跟随法和图论法[7]、Khatbi等提出的人工势场法[8],以及Ren等提出的虚拟结构法[9]。典型的成果有英国的JAYDE和美国的VIJAY用控制矩阵和状态转换图来实现编队的变化[10-11],国内有沈阳自动化设计的MARCAS系统和陈卫东等提出的行为融合加权法[12-13]。随着任务难度越来越大,基本的编队算法已经无法满足目前的需求,一些新的编队控制算法应运而生。
文中提出一种新的基于微粒群模型的机器人编队控制算法,该算法通过构造适应值函数,并采用微粒群算法获取适应值函数的最优解,将优化过程中的最优解作为机器人新的运动方向,并利用MATLAB软件进行仿真。
1 机器人编队优化模型
1.1 问题的描述和定义
定义一个二维连续空间表示物理环境:T2={(x,y),0≤x≤xmax,0≤y≤ymax}。
Ω为包含所有机器人的群体集合,Ω={S1,S2,…,Sn};Si表示简单智能的机器人,坐标为PSi=(xi,yi)。
(1)线形编队表示机器人与X轴横坐标的夹角为θ(θ∈(0~360°)),两相邻机器人之间的距离为常数d的队形。
(2)圆形编队表示机器人均匀排列成以极点为圆心,半径为r的圆,其中θi为第i个机器人与X轴正半轴的夹角。
(3)三角形编队表示以S1、S2和S3为三个顶点机器人排成的一个正三角形。假设机器人数量为n,定义函数round(X)表示将X四舍五入取整。
第一条边上的机器人为:A1~Around((n+3)/3);
第二条边上的机器人为:Around((n+3)/3)~Around((n+round((n+3)/3))/2);
第三条边上的机器人为:Around((n+round((n+3)/3))/2)~An,A1。
(4)六边形编队表示六个机器人排成正六边形。设机器人数量为n,每条边上从起始机器人到终止机器人的确定方法为:用S1表示第一条边的终点机器人编号,Si表示第i条边的终点机器人编号,定义符号[ ]表示向下取整。则:
Si=Si-1+[(n-Si-1)+(7-i)/(7-i)],
i=1,2,…,5,S0=0
采用分布式控制方式,将每个机器人初始化为一个微粒,每个机器人根据微粒群算法(PSO)[14]优化目标队形(线形、三角形、圆形、六边形)的位置,通过更新Pbest来获得gbest,机器人向gbest的方向运动,实现多机器人编队和队形变换。
1.2 编队优化算法
编队优化算法的基本思路是构造一个包含Ω中单个机器人位置信息的适应值函数f,将f取极小值时的变量作为目标队形的最终位置。用PSO寻找f极值中的pg(微粒迭代过程中的最好位置)作为机器人Ω的运动方向。机器人的位置和速度迭代公式如下:
(1)
(2)
式1采用闭环控制,机器人的期望位置pgi和机器人所感知到的实际位置pAi之差为误差信号∂,即∂=pgi-pAi。通过将机器人的运行速度V设定为∂的函数来驱动机器人移动到正确的位置。现设V=ω∂,ω为权值,有:
(3)
算法的总体流程如图1所示。
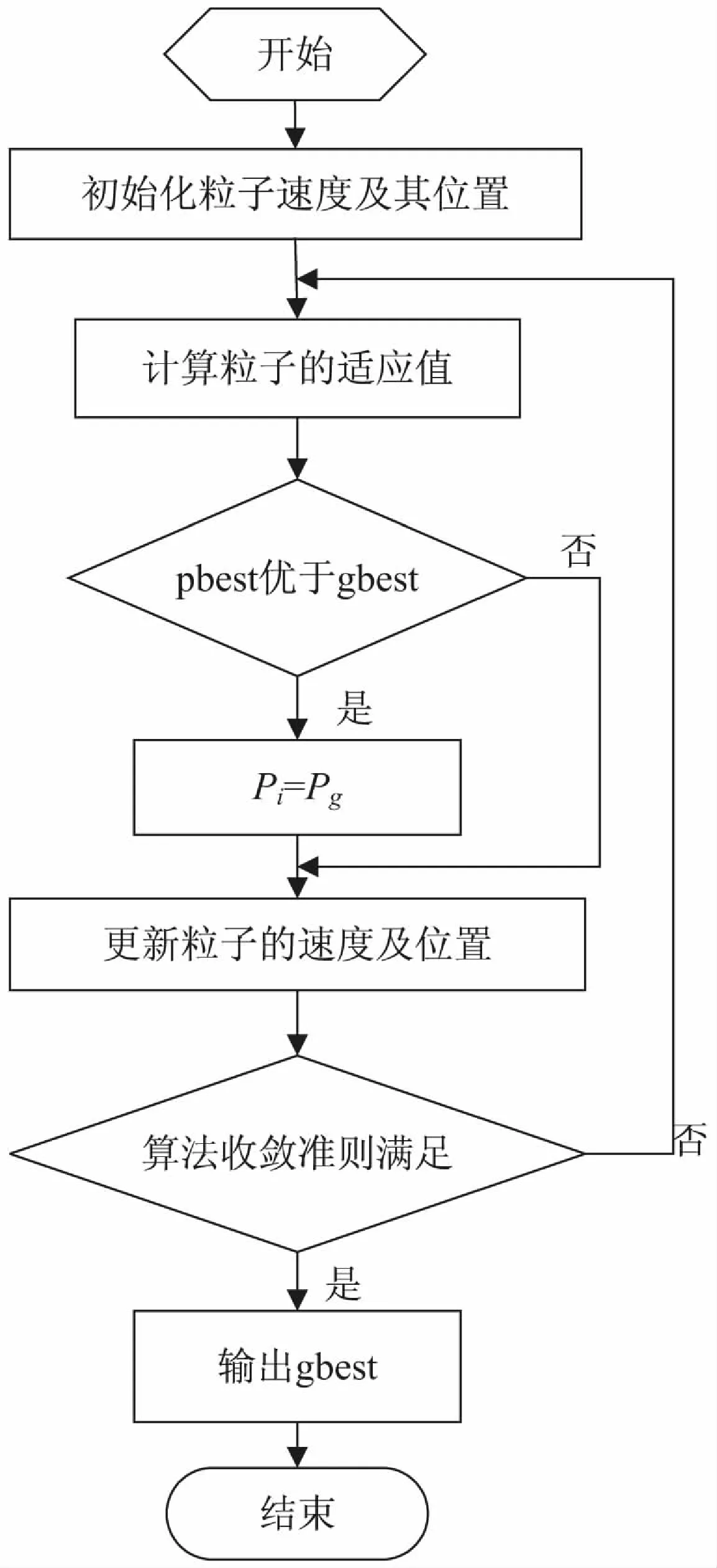
图1 算法总体流程
1.3 不同队形适应值函数的构造
(1)线形队形f如下:
f(x1,y1,x2,y2,…,xn,yn)=
(4)
其中,θ指直线与X轴正方向夹角;d指两相邻机器人之间的直线距离。
(2)三角队形f见式5,设round((n+3)/3)=p,round((n+round((n+3)/3))/2)=q。
f(x1,y1,x2,y2,…,xn,yn)=
[d1sinθ1-(yi-yi+1)]2}+
[d2sinθ2-(yj-yj+1)]2}+
[d3sinθ3-(yk-yk+1)]2+
[(d3cosθ3-(xn-x1)]2+
[d3sinθ3-(yn-y1)]2}
(5)
其中,di为第i条边上相邻机器人之间的距离;θi为第i条边与X轴正方向的夹角。通过调整f中的di,θi即可得到任意形状的三角形。若为正三角形,则θi=θi-1+2π/3,i=2,3。
(3)圆形队形是以极点为圆心,r为半径的圆,适应值函数为:
(4)六边形适应值函数如式7所示:
f(x1,y1,x2,y2,…,xn,yn)=
[d1sinθ1-(yi-yi+1)]2}+
[d2sinθ2-(yj-yj+1)]2}+
[d3sinθ3-(yk-yk+1)]2}+
[d4sinθ4-(yl-yl+1)]2}+
[d5sinθ5-(ym-ym+1)]2}+
[d6sinθ6-(yi-yi+1)]2+
[d6cosθ6-(xn-x1)]2+
[d6sinθ6-(yn-y1)]2}
(7)
其中,di指第i条边上相邻机器人之间的距离;θi指第i条边与X轴正方向的夹角。通过调整f中的di和θi可以得到任意形状的六边形。正六边形为θi=θi-1+π/3,i=2,3,4,5,6。
2 队列变换策略
2.1 线形与三角形的变换
线形变三角形:根据机器人个数n计算出S1和S2,S1~S2的机器人位置不变;1~S1-1的机器人以S1为参考点排成直线,斜率θ1=θ+2π/3,θ为原直线的斜率;目标函数如式8所示。编号S2+1~S1的机器人以S2为参考点排成直线,直线斜率θ2=θ+π/3,目标函数如式9所示。
f(xs2+1,ys2+1,xs2+2,ys2+2,…,xs,ys)=
[(i-S2)×dsinθ2-(yi-yS2)]2}
(8)
f(x1,y1,x2,y2,…,xs1-1,ys1-1)=
[(s1-i)×dsinθ1-(yi-ys1)]2}
(9)
三角形变线形:S1~S2的机器人保持位置不变,以S1和S2所在直线为另外两条边的斜率形成直线形。使用前面提到的直线形编队进行优化。
2.2 三角形与圆形的变换
三角形变圆形:将1、S1、S2三个机器人的重心o作为极点,圆的半径r可根据需要选择,取所有的机器人到重心的平均距离作为r。机器人的速度和位置迭代公式如式10和式11所示,其中di为机器人到重心的距离。
Vi+1=g×(Xi-O)×(r-di)
(10)
Xi+1=Xi+Vi+1×Δt
(11)
圆形变三角形:根据x=r×cosθ和y=r×sinθ将极坐标系转化为直角坐标系,通过n计算S1和S2,则1、S1、S2成为三角形的三个顶点。再用式12和式13将两顶点之间的机器人运动到两顶点所在直线上,其中o1、o2为两顶点的位置,n1为两顶点间机器人的个数。
(12)
Xi+1=Xi+Vi+1×Δt
(13)
2.3 圆形与六边形的变换
圆形变六边形:根据n1计算出S1~S5,则1,S1~S5变成六边形的六个顶点。用式14和式15将两顶点之间的机器人运动到两顶点所连成的线段上,其中o1、o2为两顶点的位置。
(14)
Xi+1=Xi+Vi+1×Δt
(15)
六边形变圆形:极点为1,S1~S5六个机器人的重心o,根据式16和式17更新机器人的速度和位置,其中圆心半径r为所有机器人到重心的平均距离,di为机器人到重心的距离。
Vi+1=g×(Xi-o)×(r-di)
(16)
Xi+1=Xi+Vi+1×Δt
(17)
3 仿真实验结果
3.1 不同形状编队仿真
图2(a)是线形仿真,n=7,θ1=5π/6,d=10时,迭代了528次。图中星号表示初始位置时机器人的团队重心。图2(b)是三角形仿真,n1=12,θ1=π/3,边长为60时,迭代1 844次的结果。图2(c)是圆形仿真,n=10,r=15时,迭代2 076次的结果。图2(d)是六边形仿真,n=20,边长为40,θ1=π/3时,迭代4 101次的结果。
表1表示在不同机器人个数下对四种队形编队仿真时,算法执行50次的平均迭代次数、最好迭代次数和最坏迭代次数,以及迭代失败次数和迭代次数的方差。
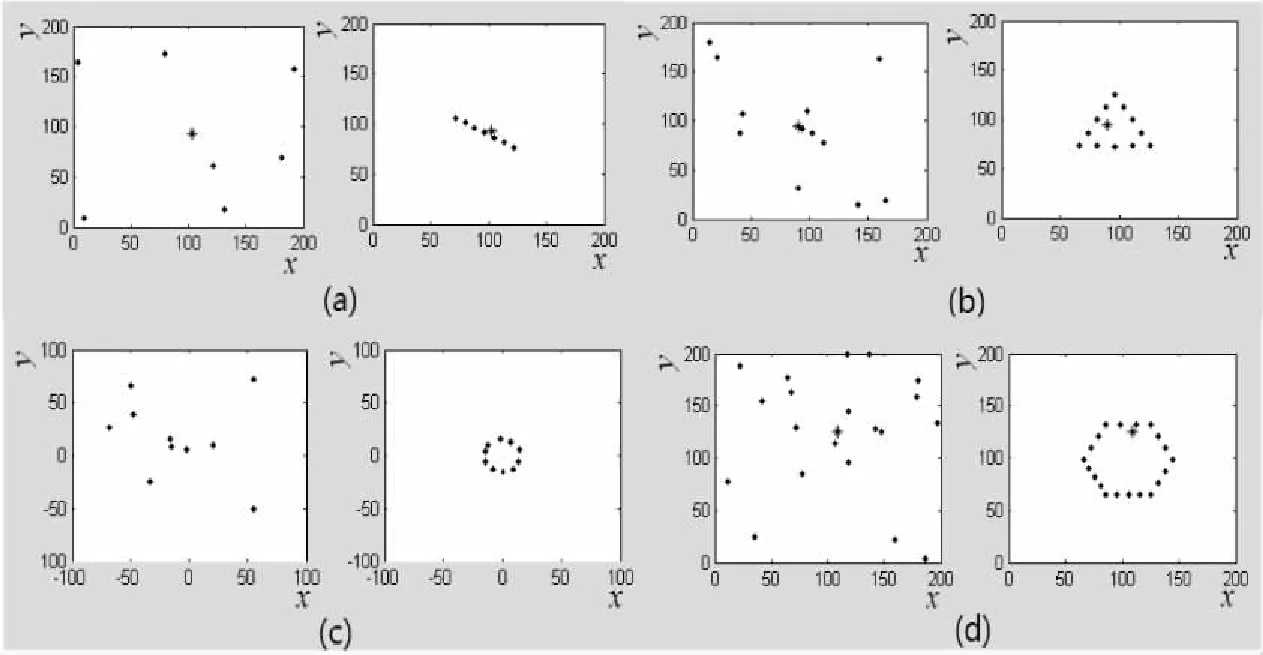
图2 线形、三角形、圆形、六边形仿真
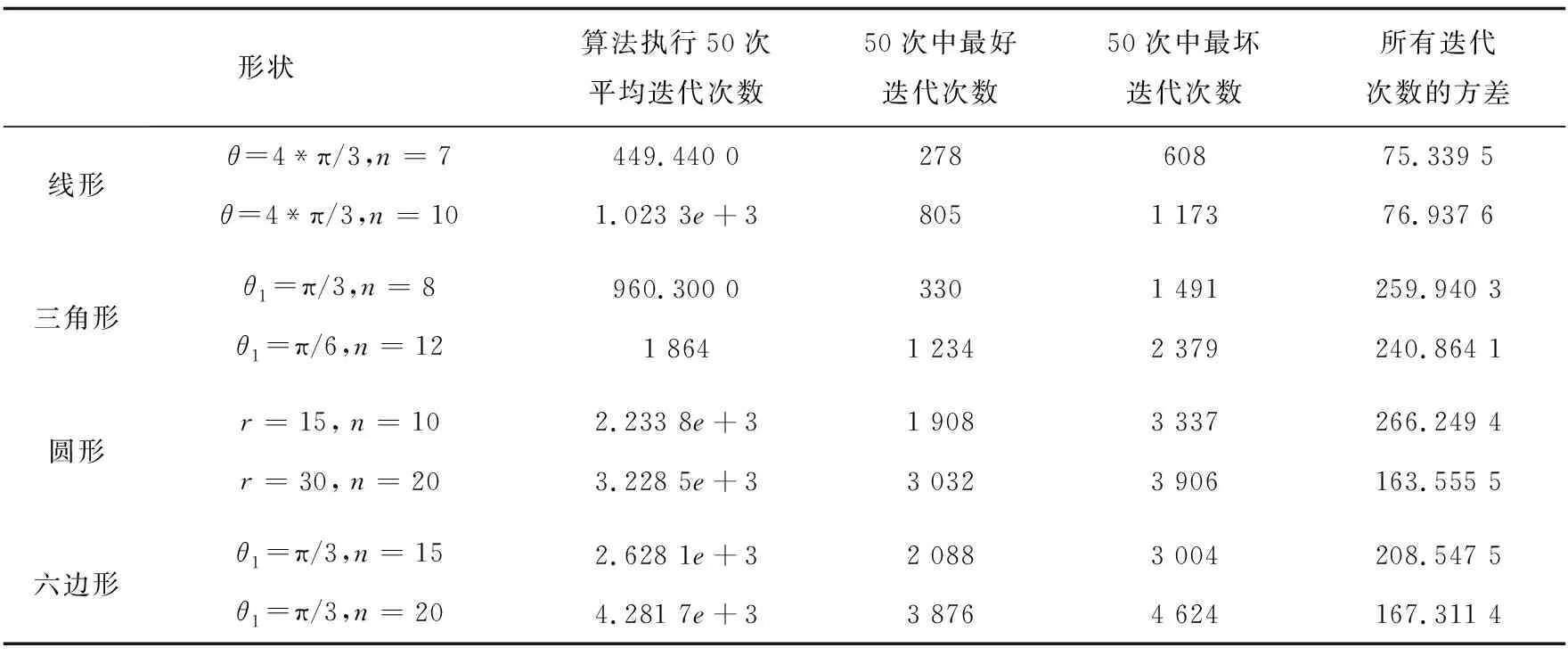
形状算法执行50次平均迭代次数50次中最好迭代次数50次中最坏迭代次数所有迭代次数的方差线形θ=4*π/3,n=7449.440 027860875.339 5θ=4*π/3,n=101.023 3e+38051 17376.937 6三角形θ1=π/3,n=8960.300 03301 491259.940 3θ1=π/6,n=121 8641 2342 379240.864 1圆形r=15,n=102.233 8e+31 9083 337266.249 4r=30,n=203.228 5e+33 0323 906163.555 5六边形θ1=π/3,n=152.628 1e+32 0883 004208.547 5θ1=π/3,n=204.281 7e+33 8764 624167.311 4
3.2 四种形状队形变换仿真
图3机器人数量为10,s1=4,s2=7。(c)、(d)的点为s1与s2之间的机器人。图(a)的线形到图(b)的三角形,迭代次数为95,运动轨迹为(c)。从图(b)的三角形到图(a)的线形,迭代次数为88,运动轨迹为图(d)。
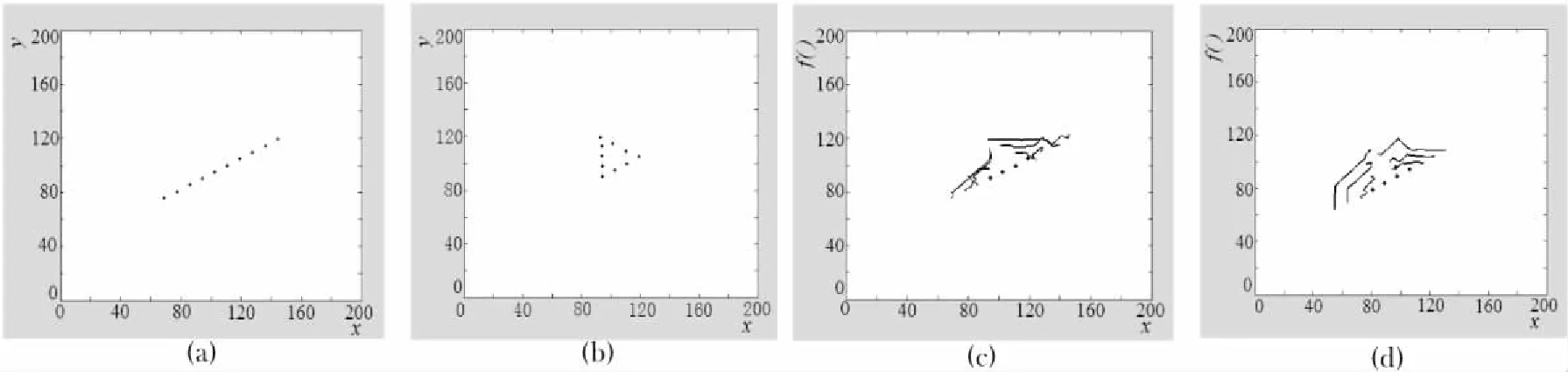
图3 线形和三角形变换
图4中的机器人数量为20个,迭代次数为100,仿真中机器人是直接运动到目标点的。
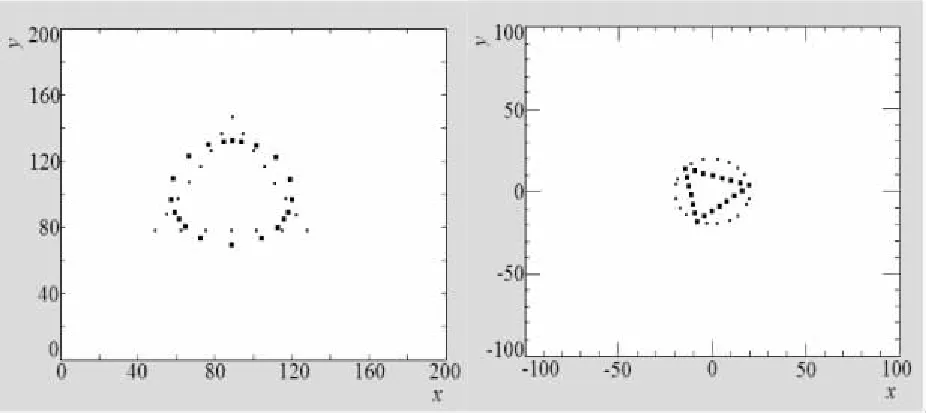
图4 三角形与圆形的变换
图5中机器人数量为18个,固定迭代次数为100。图5是圆形与六边形的变换。

图5 圆形与六边形的变换
从仿真结果可以看出,利用该计算方法能快速地实现多机器人编队和队形变换,自组织编队形成的目标队形重心与机器人初始化时的重心距离不远,从而体现了PSO算法优化的魅力。
4 结束语
提出了一种基于PSO的分布式编队控制算法。仿真结果表明,与集中式控制相比,分布式控制方式可以独立考虑每个机器人的特性,具有较强的灵活性、鲁棒性等优点。而采用PSO算法可以很快地达到适应值,收敛速度更快,迭代次数更少,有效提高了编队效率。但是文中研究的多机器人编队是静态的,如何让机器人动态编队完成跟踪任务还需要进一步研究;并且文中只考虑二维平面的机器人编队,编队过程中没有考虑障碍物,因此以后可以加入障碍物并从二维扩展到三维[15]进行研究。
