基于排队论的工业无线传感网超帧结构研究

许浩然，刘广钟

(上海海事大学 信息工程学院，上海 201306)

0 引 言

工业物联网是物联网架构的基础，连接了物理世界中的各种信息和信息处理系统。工业无线传感器层位于最底层，负责数据的采集和实施等，中间是逻辑控制层，负责数据传输，最上层是互联网层，负责将采集到的数据进行语义分析并返回处理结果[1]。

工业物联网与传统物联网的区别在于，工业物联网需要考虑更多的紧急情况和安全性，一些实时闭环控制和开环控制，开环控制包括人工的控制，信息的上传和下载等，闭环控制则是完全的机器控制。所以工业物联网对数据包的实时性和准确性要求很高。不同的工业应用场景的数据采集周期不同也会造成数据包的传输延迟和信道占空比不同[2]。

文献[3]提出了一种基于WIA-PA工业无线传感器网络的自适应调度型MAC协议，该协议通过对WIA-PA超帧结构进行改进，使设备在接入网络的过程中，网络管理器根据网络中数据吞吐量的实时变化情况，自适应地调整超帧结构中各阶段的长度，合理地分配通信资源。文献[4]研究了排队论模型预测局部路由节点的最佳休眠时间，从而增强了路由节点的低功耗性能。文献[5]研究了排队论在数据包延迟模型中的应用，将延迟分为三部分，第一部分是从数据包产生到节点本地缓存队列头的延迟，第二部分是队列头到竞争得到时隙时的延迟，第三部分是数据包的传输延迟。文献[6]使用OPNET仿真软件建立了带GTS机制的分析仿真模型,分析了在不同超帧级数SO下，帧传输速率和缓冲容量对GTS机制下的网络吞吐量和延时的影响，结果表明对于低传输速率和低缓冲容量的工业无线传感器网络,选取合适的SO值(SO=2或3)，带GTS的分配时隙机制更适合用来提升网络利用率和系统实时性响应。文献[7]详细说明了三种工业物联网超帧结构(WirelessHART[8]、WIA-PA[9]、ISA100.11a[10])的区别，并使用排队论为三种超帧结构建立统一数学模型，开发了仿真实验工具。实验证明在不同实验设备下，GTS时隙数目不同延迟也不同。在没有GTS时隙时延迟最低。

针对IEEE802.15.4e中的WIA-PA超帧，文中详细分析其结构，并利用排队论为超帧中的CAP和CFP阶段建立模型，使用仿真工具模拟实验，分析数据包延迟原因，以及如何降低数据包延迟。

1 超帧模型

在IEEE802.15.4e中，针对工业物联网提出了三种超帧结构：WirelessHART、WIA-PA和ISA100.11a。WIA-PA是其中最常用且最具代表性的超帧结构，如图1所示，其原理类似于时分复用技术(TDMA)[11]。但不同的是超帧分为两个时间段：活跃期和非活跃期。在非活跃期内，协调器进入低功耗模式(即睡眠模式)。节点仅在活跃期间通信，在活跃期内分为两个阶段：竞争区(contention access period，CAP)、非竞争区(contention-free period，CFP)。在竞争区中，因为时隙数目有限，无法保证所有节点都能分配到一个时隙，所以每个时隙都被所有的设备共享，设备都需要通过竞争的方式来获取该时隙的使用权限，但是该时隙并不保证数据发送的成功与否；如果失败，则使用载波监听多点接入与冲突避免(CSMA/CA)机制重传数据。在非竞争区中，划分若干个确保时隙(GTS)，每个设备需要申请使用确保实隙(GTS)，可以是一个或多个时隙，具体数目在申请使用时确定。非竞争区通常被用来发送比较紧急的数据，满足数据包的延迟要求。

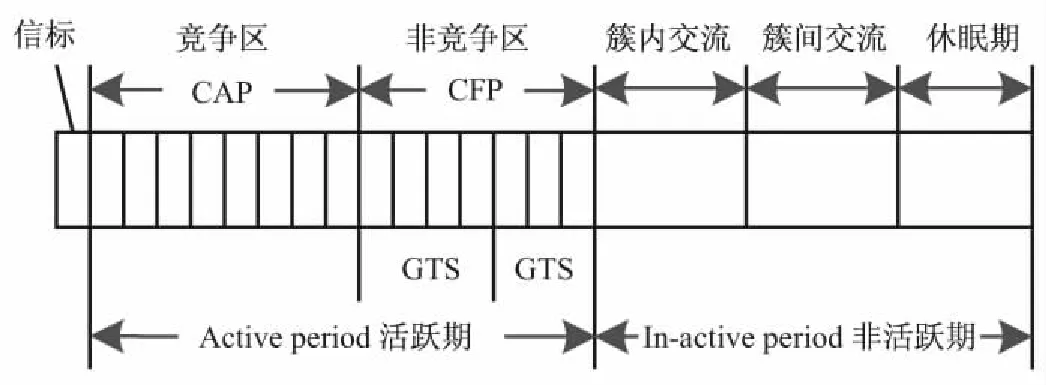
图1 WIA-PA超帧结构

超帧中规定非竞争时段必须跟在竞争时段后面[12]。竞争时段的功能包括网络设备可以自由收发数据，域内设备向协调器申请GTS时段，新设备加入当前PAN网络等。非竞争阶段由协调者指定的设备发送或者接收数据包。如果某个设备在非竞争阶段一直处在接收状态，那么拥有GTS使用权的设备就可以在GTS阶段直接向该设备发送消息[13]。

CAP和CFP合在一起称为活跃期，该活跃期被平分为16个时隙，信标帧总是开始于第一个时隙的开头，CFP中有最多7个GTS。超帧结构由协调器定义并且在网络层中使用请求原语进行配置，两个连续信标间的持续时间(BI)，由数值macBeaconOrder(BO)属性和aBaseSuperframeDuration常量决定。

BI=aBaseSuperframeDuration*2BO

(1)

在一个信标使能的网络中，BO可以是0～14中的任何值，如果BO的值被设置为15，网络将被认为是非信标使能，并且不使用任何超帧。

超帧活跃时间段的时间叫做超帧持续时间(SD)，由式2计算得出。

SD=aBaseSuperframeDuration*2SO

(2)

其中，SO是macSuperframeOrder属性的值。超帧持续时间SD不能超出信标间隔BI，因此，SO的值总是小于或等于BO。上述常量数值由IEEE 802.15.4 standard document提供。

在工业无线传感器网络中，底层传感器节点感知信息产生数据包，通过向协调器发送请求竞争使用超帧的CAP或者CFP来发送数据，申请成功则立刻发送数据，如果没有申请成功，则放在节点本地的缓存中排队，等待下一轮申请，所有节点都遵循该规则。

超帧的结构与普通的排队不同，每个超帧的周期都会有不同数目的时隙用来发送数据，相当于在排队论中的服务台，但又不是同时运作，在超帧的结束有一段睡眠期，这段时期可以看作是服务台的轮转调度期。文中采用数学工具排队论来为超帧建模，评估超帧系统性能，降低数据传输延迟，提高信道利用率。

2 排队论模型

根据实际情况，假设共有m个传感器节点，并且每个节点数据包的产生服从参数为λ的泊松分布。根据相关研究背景，假设数据包的平均服务时间服从参数为μ的负指数分布(服务时间=等待时间+发送时间)[14]，传感器节点本地缓存有限，即队列长度有限，数据包采用先来先服务的原则(FCFS)，有c个时隙用来发送数据(0≤c≤16)，即有c个服务台，这种模型记为M/M/c/N/∞/FCFS排队模型。

m个传感器节点所产生的数据都需要竞争来使用CAP或者等待协调器安排使用CFP中的GTS来发送。如果申请使用CAP成功，则进入数据包发送阶段，延迟由数据包传输速度决定，如果没有申请成功，则需要在本地缓存中等待下一轮竞争，直到数据包得到时隙，或者时效时间过期丢弃该数据包，将数据包从本地缓存清除[15]。另外一些符号在表1中详细给出相应含义。

表1 符号含义

传感器节点、协调器、缓存、数据包等综合称为一个系统，整个系统能平稳运行是要满足一定条件的，即系统不能产生无限长的等待队列。

因为假设CAP数据包的产生服从泊松分布，而CFP的数据包所占比例是比较少的，并且CFP的数据包传输不需要排队，所以CFP中的数据包延迟仅包含数据包在超帧中的传输时间。在CAP阶段还存在数据包发送不成功的情况，延迟模型采用CSMA/CD技术来保证发送失败数据的重发。

在延迟分析时加入CFP段的数据传输部分延迟，更加全面合理地模拟超帧延迟。系统中的总数据包数量记为Ls，所有在节点本地缓存排队的数据包数量和记为Lq，那么就有Ls=Lq+超帧中的数据包，这里超帧中的数据包包含CAP和GTS的数据包。

数据包从产生到发送完成的总时间记为Ws，数据包从产生到获得时隙延迟时间记为Wq，那么就有Ws=Wq+数据包在超帧中的时间，数据包在超帧中的时间即是数据包的发送延迟，Ws称为等待延迟。

pn表示系统中有n个数据包的概率，需要满足:

(3)

采用时齐的马氏链来分析状态转移过程，若满足P{Xn+m=j|Xn=i}=Pij(m)，则称{X(n),n=0,1,2…}为时齐马氏链，Pij(m)是系统i经过m个时间间隔(或m步)转移到状态j的转移概率。文中假设超帧系统p服从齐次马氏链过程，以下过程均基于此假设。

整个系统的状态转移图如图2所示，根据此图可得该状态转移方程为：

(4)

此状态转移方程表示系统中的数据包产生和发送平衡。n=0表示初始状态的平衡方程，1≤n≤c表示系统中的数据包还没有到达时隙的上限，数据包的发送率根据n的变化而变化，n>c表示系统中请求使用时隙的数据包已经超过时隙本身的限制，新产生的数据包很大部分可能需要排队来等待竞争使用时隙，所以这时的节点发送率均为cμ。而数据包的产生率则一直为mλ。

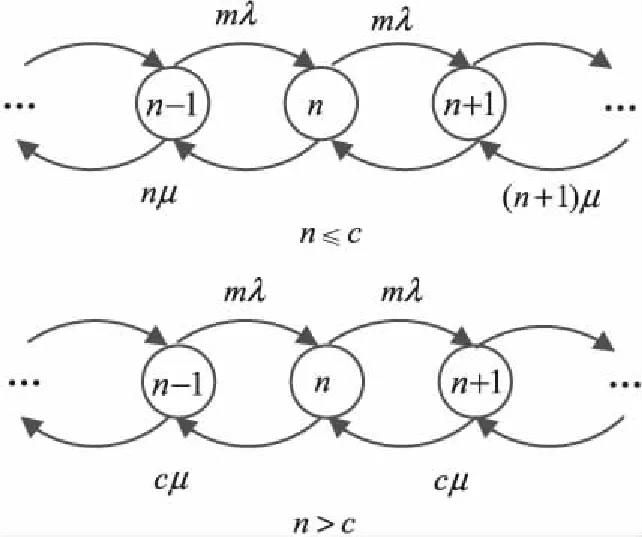
图2 状态转移图

使用递推法解此差分方程得：

(5)

其中，p0表示系统中没有任何数据的概率；pn表示系统中有n个数据包的概率。

当系统中的数据包数目大于时隙数目c，则新产生的数据包必须等待，节点产生的数据包必须等待的概率为：

(6)

(7)

系统中的平均队长为：

(8)

可以证明，Ws是服从cμ-mλ的负指数分布，并根据排队论中的Little公式，数据包在系统中的停留时间和在队列中的等待时间分别是：

(9)

上述指标是根据排队论来建立的超帧系统模型，在实验分析过程中会对比理论延迟和实际延迟之间的差别。文中把数据包产生到本地缓存队列头的延迟和到达队列头再到竞争得到时隙时的延迟合起来称为等待延迟，并加入了数据包在超帧中的发送延迟，因为数据包在超帧中的延迟并不是忽略不计的，如果数据包发送失败，数据包则会重新排队产生较大延迟。文中详细给出了数据包必须等待的概率、队长、正在发送的数据包数目等重要指标。

3 单队列超帧结构

上述模型是基于每个节点都有自己的缓存队列，文中根据此模型提出一种优化的单队列超帧传输方式，每个节点产生的数据包发送到协调器上的缓存来排一个队列，节点自身只有数据包的备份，如果规定时间内没收到确认到达回复，源节点重新发送该数据包；收到确认数据包，则发送成功。理论上该方法只会增加协调器的工作能耗，但是会提高整体网络的利用率，降低数据包的延迟，因为竞争使用超帧的队列只存在于协调器上，单队列的运行原理如图3所示，利用排队论来分析两种模型的差别。

与上一节中的多队列模型相比，单队列结构更加简单高效，可引用排队论中的M/M/1模型分析计算系统的延迟。p0和pn分别为：

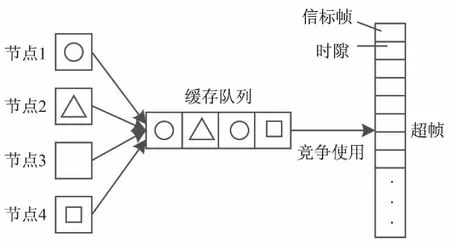
图3 单队列模型

(10)

数据包的逗留时间为：

(11)

队列中的等待时间为：

(12)

对比多排队模型，单排队模型减少了队列数目，提高了数据发送率，在节点数目较多时降低了数据传输延迟，并且减少了节点的成本，把每个节点的自身缓存降到最低，使得节点能更加高效地将有限的处理能力用到数据采集和处理上面。再者有的节点处于复杂环境中，或者本身采集的数据周期长，导致自身缓存大量浪费，此时这种优化模型就可以提高缓存的利用率。

4 实验与分析

文中利用MATLAB R2014a工具来模拟实验，首先对比理论计算得到的延迟和实际测出的延迟差别，统一假设λ=5，数据包处理速率μ=5，CAP为12个，2个GTS，每个GTS占用2个时隙，GTS段的延迟时间忽略不计，因为仅有少量的传播延迟没有排队延迟[16]，所以不是实验的评估重点。

为了证实单队列模型确实优于多排队超帧结构，利用第三节中的延迟模型来对比两种排队模型数据包的延迟。使用MATLAB计算实验结果的数据，根据控制变量法，首先对比在不同的节点数目下，相同的数据包产生频率(λ=5，为了使结果的对比性更加完整，数据包处理速率取μ=5，CAP为12个，2个GTS，每个GTS占用2个时隙)。多队列模型每个节点的缓存大小是3个时隙，优化后模型的单队列大小是3m个时隙，这是为了比较两种模型在排队方式不同外，其余条件都相同下的平均数据包延迟。

通过图4可以看出，在节点数目为14以前，优化前的模型与优化后的模型延迟相差不大，但是从16个节点数目开始，优化后的模型明显比优化前的模型延迟低，理论上分析为节点数目较少时，多队列与单队列的效果并不明显，相差不大。但是在节点数目增加时，多队列的延迟明显增加，因为每个队列在竞争不到超帧时隙的时候都会形成一个等待队列，当所有的队列都在等待时，协调器需要为每个队列根据需要来分配时隙。但是在单个队列中，协调器会提前根据需要在队列中竞争分配时隙，效率比所有的队列单独申请时隙高，所以在节点数目增加后，多队列的线性模型斜率比优化前多队列的斜率低，所以在节点数目较多的情况下，优化后的单队列模型做到了降低延迟。

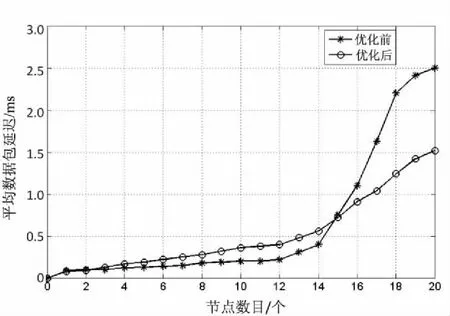
图4 不同节点数目对比

其次固定其他数据，只改变时隙数目，观察时隙数目c从1到16时的延迟变化，设置m=15,λ=5,μ=5。实验结果如图5所示。可以看到，在时隙数目比较少时优化前后的差别不大，因为在只有少数几个时隙的时候，队列的多少并不影响整体的延迟，而在时隙数目增加时，就可以看出优化后的单队列模型延迟低于优化前的多队列模型延迟。

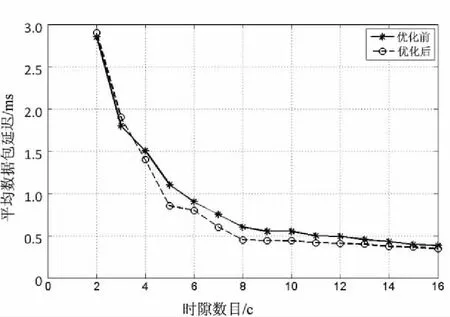
图5 不同时隙数目对比

在文献[7]中得到的结果是没有GTS时隙时，整体网络的延迟是优于GTS和CAP同时存在时的混合模型，文中实验也验证了这一结果，时隙数目较少时延迟较高。所以CAP的时隙数目越多，网络延迟越低。

5 结束语

文中利用排队论为工业无线传感器网络中的超帧结构建立了新的数学模型，根据该数学模型，提出了一种优化的单队列超帧结构，在节点数目较多时降低排队延迟，并通过分别设置节点数目和时隙数目为自变量进行模拟实验。通过实验结果对比，验证了优化模型的正确性，提升了超帧数据的传输效率，满足了工业无线传感器网络的实时性要求。