室内可见光通信高精度定位系统设计

许毅钦, 陈志涛, 袁 涛， 陈 昊， 古志良, 张志清, 张 强， 许 平， 陈俊芳*

(1. 华南师范大学 物理与电信工程学院, 广东 广州 510640;2. 广东省半导体产业技术研究院, 广东 广州 510650; 3. 华南理工大学, 广东 广州 510650)

1 引 言

近年来，发光二极管由于其长寿命、高亮度和快响应的特性被广泛用于区域照明、车灯和交通信号灯等相关产品。可见光通信技术(Visible light communication,VLC)是基于LED的新一代通信技术，通过控制LED的快速开关达到通信的目的。目前在国际上，由于VLC技术的高速、保密性好、无需占用无线电频谱资源的特点而广受关注[1]。作为一项新兴技术，目前VLC在许多领域已有相关的应用报道，如水下通信[2]、超高速光组网[3-7]、室内定位[8-10]等。

在室内环境中，由于建筑物材料对电磁波的吸收及钢结构的电磁波屏蔽效应，GPS等基于电磁波的定位系统会产生较大的定位误差[11]。为此在室内定位领域，已有许多补充定位技术被提出，如射频标签(RFID)[12]、视觉定位技术[13]、Wi-Fi定位技术[14]等。已经有相关文献报道这些室内定位技术的应用，然而上述的室内定位技术仅能实现1～5 m的室内定位精度。相比于户外环境，室内定位往往需要更高的定位精度以实现位置信息相关的推送服务，因而上述的室内定位解决方案尚未完全满足实际需要。

而基于可见光通信技术的室内定位系统由于无需借助电磁波通信，可实现室内高精度定位。目前国际上已有许多文献报道了基于VLC的室内定位技术。若不考虑附加的精度控制技术，基于VLC的室内定位算法可分为接收信号强度(RSS)、到达时间差(TDOA)、到达接收角(AOA)、到达相位差(PDOA)[15-17]。在上述系统中TDOA与PDOA可实现较高的定位精度，但是系统需要时钟同步处理，系统的复杂度较高，不利于系统集成。而AOA是基于角度的定位算法，需要特制的传感器测量信号到达角。RSS通过测量信号强度来估计相对距离，无需额外的设计，然而由于信号强度的采样值通常受到信道的多径效应、系统噪声影响，在上述的几种定位算法中，RSS的定位精度最差。

由于基于RSS的室内可见光定位系统复杂度低、易于实现且成本很低，因而具有广阔的应用前景。为了解决基于RSS算法的室内可见光通信定位系统精度不足的问题，本文提出一种基于人工神经网络和迭代优化算法的RSS室内可见光通信定位系统的设计方案，包括硬件部分及算法。首先通过训练人工神经网络，使得网络拟合室内的直射信道及漫射信道，消除由于多径效应引起的信号强度采样误差。不同于信道的静态参数，由于噪声是随机过程，无法采用学习的方式进行拟合，因此进一步通过优化算法降低由于噪声等随机过程引起的定位误差。

2 可见光通信室内定位系统原理

2.1 信道模型

基于可见光通信技术的室内定位系统由安装在天花板上的LED(CREE Q5 XPE 3 W)及接收机组成。模型中接收机包含一个光电二极管(PD)一级跨阻放大电路。由于LED的尺寸与实际光信号的传输距离相比较小，因此常将LED当作朗伯体进行分析。

如图1，将LED的发射角定义为θ，LED与光电二极管之间的空间距离定义为d,直射光信号与光电二极管法线之间的夹角定义为φ。直射信道模型描述了发射机与接收机之间的光信号传输特性，其传输函数可以写为：

H(0)LOS=

式中A为光电二极管的有效感光面积，Ts(φ)为光滤波器增益，G(φ)为聚光透镜增益，mt、mr为朗伯常数。

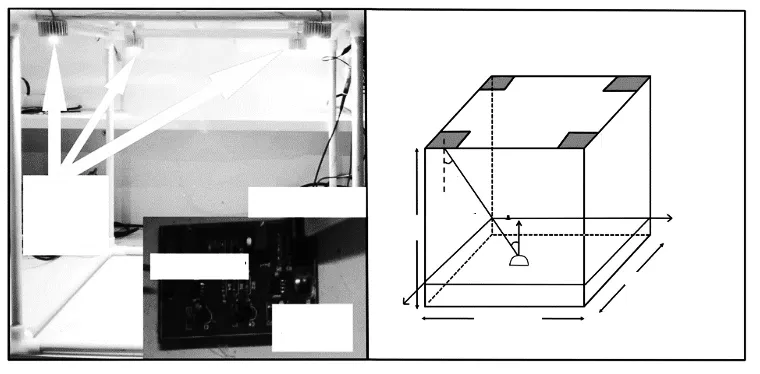
图1 可见光通信室内定位系统模型图

Fig.1 Model of positioning system for indoor visible light communication

通常室内的可见光通信不是理想的直射链路信道，由于墙壁、地面及室内其他具有反射特性物体对光信号的漫反射作用，会产生多径效应。漫反射信道的传输函数可以写为：

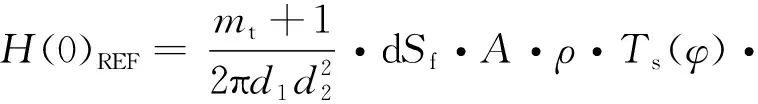
cosα·cosβ·cosmt(θ)·cosmr(φ)， (2)

式中d1、d2分别为LED到反射点及反射点到接收机之间的距离，ρ是与反射体材料有关的系数，dSf为反射体的面积微元，α、β分别为反射光信号的入射角与出射角。

如果设接收机接收到光信号的功率为Pr，单个LED的辐射功率为Pt，则接收功率与辐射功率之间的关系可以表示为：

Pr=PtHLOS(0)+PtHREF(0)dSf.(3)

现有的一些基于RSS方法的室内可见光通信系统设计仅仅考虑了直射链路信道增益函数，并通过一些纠错算法可实现的定位精度普遍在3～10 cm[18-20]。而漫射信道由于室内情况复杂，几乎无法通过解析的方式计算其附加增益。同时实际接收到的信号功率还与系统噪声因素相关，一般考虑电路系统及光路系统噪声：(1)由光信号及背景光信号造成的散粒噪声;(2)电路元件热噪声。这两类噪声均可视为加性高斯白噪声：

在这些公式中,q、B、k、Ibg、Tk、G0、Γ、η、gm分别为元电荷电量、等效噪声带宽、波尔兹曼常数、背景光电流、绝对温度、电路开环电压增益、信道噪声常数、光电二极管的固定电容量和跨导。

2.2 硬件系统原理

为了解决室内多参考点可见光通信带来的码间干扰问题，需要引入多址技术[21]。本系统使用码分多址技术(CDMA)用于码间干扰的消除，具体做法如下：

(1)每个LED获得事先约定的二进制ID信息码序列(代表所在的地理位置)，该序列用于区分不同的LED信号源，第i个LED的二进制ID信息码序列可以写为：

Si={Si,1,Si,2,…,Si,N}.(6)

(2)产生OOK调制的ID信息码基带信号。

(3)直接扩频调制，在本系统中利用Walsh码作为扩频码，在一个具有n个信源的CDMA通信系统中需要用到长度为n的Walsh码，Walsh码可以由哈达玛矩阵产生，一个具有2n个元素的哈达玛矩阵可由迭代关系求出：

将具有2n个元素的哈达玛矩阵按每行或每列取出，可获得一组长度为n的Walsh序列：

Wi={Ci,1,Ci,2…,Ci,n}，(8)

直接扩频操作只需将每个ID信息码元与该组Walsh序列相乘，第i个LED的ID信息码扩频后的信号为：

(4)扩频后的信号经过LED驱动电路以光信号的形式发射，根据上述的室内无线光通信信道模型，并假设系统中所有的LED功率相同为Pt，接收机接收到的混叠光信号可以表示为：

根据Walsh码的正交性质：

假想接收机需要恢复第iLED的信号的第j个码元，只需要使用与扩频操作相同的Walsh序列即第i个Walsh序列对r的第j个元素进行内积运算：

Oi,j=〈Wi·r〉j=

n为系统中LED的总数，为已知量，可见从混叠信号中恢复出了光强衰减信息与不同LED的ID信息。

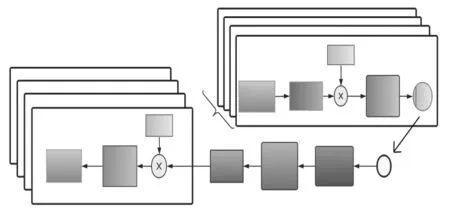
图2 可见光通信室内定位系统的框架

2.3 定位算法原理

2.3.1 人工神经网络空间距离预测算法

为了确定接收机在三维空间中的坐标(x,y,z),需要通过测量来自各个LED的信号强度从而估计接收机的空间坐标，如果先不考虑噪声等随机过程对定位结果的影响，设在接收端测得来自第i个LED参考点光信号衰减传输系数为H(i)(0)，在理想的无噪声条件下，最终的定位结果(x,y,z)是光信号衰减传输系数的H(i)(0)的非线性函数，包含了上述直射信道增益及漫反射信道增益。

目前大多数文献仅仅考虑直射信道增益对接收信号的强度贡献，这是因为在大多数情况下室内材料对光信号的吸收作用及接收机的视场角的有限性，由漫反射带来的定位误差通常可不计入考虑。然而在多反射材料(光滑的瓷砖，玻璃等)存在的室内环境，由于漫反射导致的定位误差则会对基于RSS三角方法的可见光室内定位系统造成较大的定位影响。现不考虑信道参数的具体解析表达式，通过对神经网络进行训练，使之拟合实际信道环境。

为了拟合实际信道的传输函数，我们设计了一个3层的BP神经网络，在本实验中采用了4个LED实现三维定位，为此输入层的输入是一个长度为4的向量：

I={H(1)(0),…,H(4)(0)}，(13)

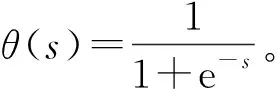
D={d(1),…,d(4)}，(14)

具体的训练算法步骤如下：

(1)获取训练样本(I(k),D(k))，其中k为样本的标号，且I(k),D(k)∈R1×4。

(2)神经网络权值随机初始化。

(3)对于每一个训练样本，从前向后计算每个神经元的输出，直到输出层。并设第i个输出层的输出值为oi。

(4)对输出层神经元计算输出误差：

δi=oi(1-oi)(di-oi).(15)

(5)对于隐藏层单元h，计算其误差项：

δh=oh(1-oh)∑k∈outputlayerwkhδh，(16)

其中outputlayer表示输出层点集合，wji表示结点i到j的连接权值。

(6)更新网络权值，增量为：

Δwji=wji+ηδjxji.(17)

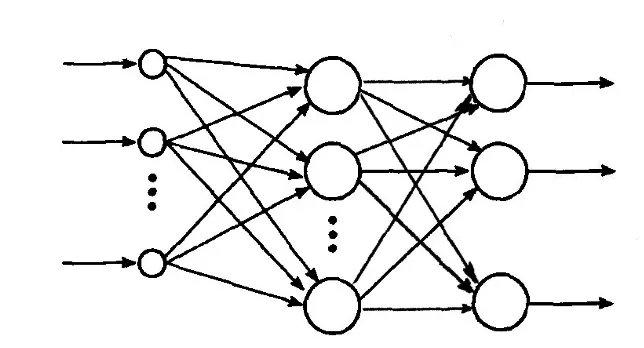
图3 用于室内定位的人工神经网络结构图

Fig.3 Structure of artificial neural network for indoor location

2.3.2 三边定位约束方程与误差修复算法

在获得了接收机到4个LED距离的估计值后，可通过下面的约束方程推算出接收机的定位估计坐标(xe,ye,ze)：

其中H是接收机与LED所在平面的垂直距离，(xi,yi)是LED的平面坐标。需要指出的是尽管神经网络能对整个室内非线性信道具有较好的拟合效果，但是无法处理诸如随机过程，如噪声因素带来的定位误差。为此提出一种基于Newton-Raphson迭代法的定位误差修复算法。算法首先假设真实的估计距离为：

其中ε(i)是随机变量且服从连续高斯分布：ε(i)～N(μ，σ2)，μ,σ2→0。做出这一假设的前提是通信的信噪比足够好，且噪声的幅度分布较为集中。误差修复算法的基本思想如下：由于噪声因素导致神经网络输出偏移正常值，结果是定位坐标(xe,ye,ze)无法同时满足方程组(16)的4个方程；从几何关系来看，以各个LED为圆心，以估计距离为半径的圆没有相交于一点(如图4)。

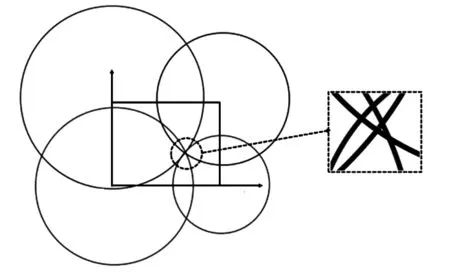
图4 噪声导致定位误差的几何描述

Fig.4 Geometric description of positioning error caused by noise

基于上述假设，约束方程可以重新写为：

并设：

定义余函数为：

fi=(xe-xi)2+(ye-yi)2-(dxy,i±ε)2，(23)

余函数对xe、ye、ε的偏导数分别表示为：

定义第k次迭代后的余函数为：

第k次迭代与第k+1次迭代之间的关系可以由以下公式表示：

根据Newton方法的原理在第k+1次迭代时余函数应当设定为0，因此上述方程可以进一步写为：

具体的误差修复算法步骤如下：

(1)选择迭代运算的初始点。

(2)根据式(23)～(25)计算余函数。

3 实验与分析

3.1 实验设计

如图1所示，在普通实验室环境搭建了室内定位实验框架，其尺寸为1 m×1 m×1.2 m。接收机高度(以光电二极管的感光面高度为基准)为0.2 m，LED光功率的参考点在框架下方0.2 m处(考虑到散热器及连接导线的高度)。在接收电路设计时，已经充分考虑OP电路的线性响应度(通过调整LED的光功率及跨阻放大倍数)，电路的最终输出波形如图5所示，信号的采样是基于STM32F407的10位ADC。具体的实验步骤如下：

(1)从坐标(0 m,0 m,0.2 m)开始以0.1 m为步长将xy平面划分为网格，以接收机在每个格点处的测量值作为样本对神经网络进行训练，共100个样本。

(2)从坐标(0.05 m,0.05 m,0.2 m)开始以0.1 m为步长将xy平面划分为网格，进行二维定位测试。

(3)以0.1 m为步长将z轴分割各平面，范围0.2～0.6 m，在每一个平面上按照(1)所述步骤

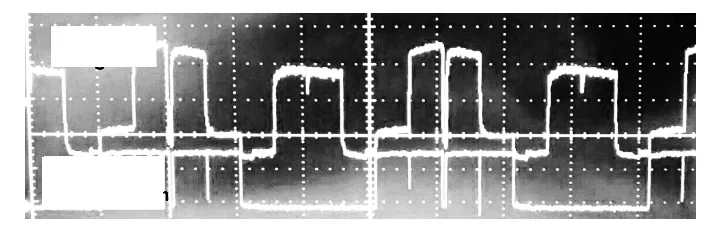
图5 CDMA接收信号波形

继续训练神经网络。

(4)在z轴0.25～0.55 m范围内，以0.1 m为步长的各个平面上按照(2)所述步骤继续训练网络，在0.3～0.5 m高度范围内进行三维随机路径定位实验。

3.2 实验结果

3.2.1 神经网络训练

图6是在一个高度平面上以100个采样点为样本的神经网络训练过程。在单次实验中，遍历整个训练集56次后，最小均方误差收敛到了预设值。单个高度平面点集的训练时间为8 s。

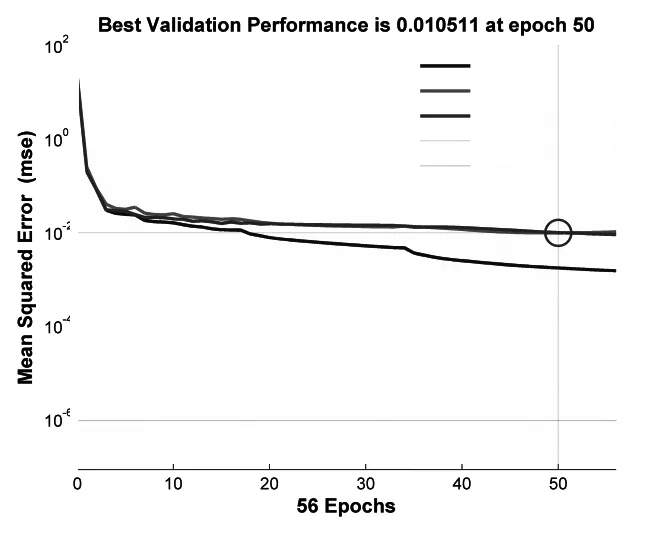
图6 均方误差下降曲线

3.2.2 二维定位实验

图7展示了二维定位的整体结果，黑色的三角形代表用于神经训练的样本数据，黑色的圆点代表用于测试的数据，白色的圆点代表人工网络的定位预测结果，从结果来看无较大的偏离，具体的统计数据展示在图9中。在100个测试点中，

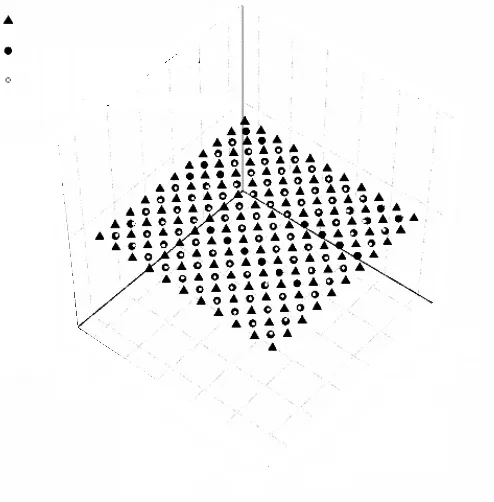
图7 二维定位实验结果

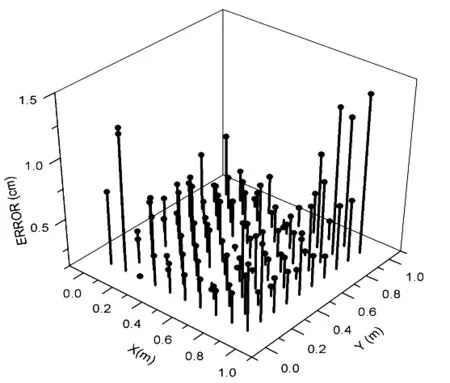
图8 二维定位误差分布

Fig.8 Two dimensional location error distribution

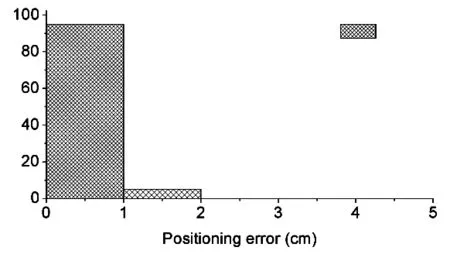
图9 二维定位误差直方图

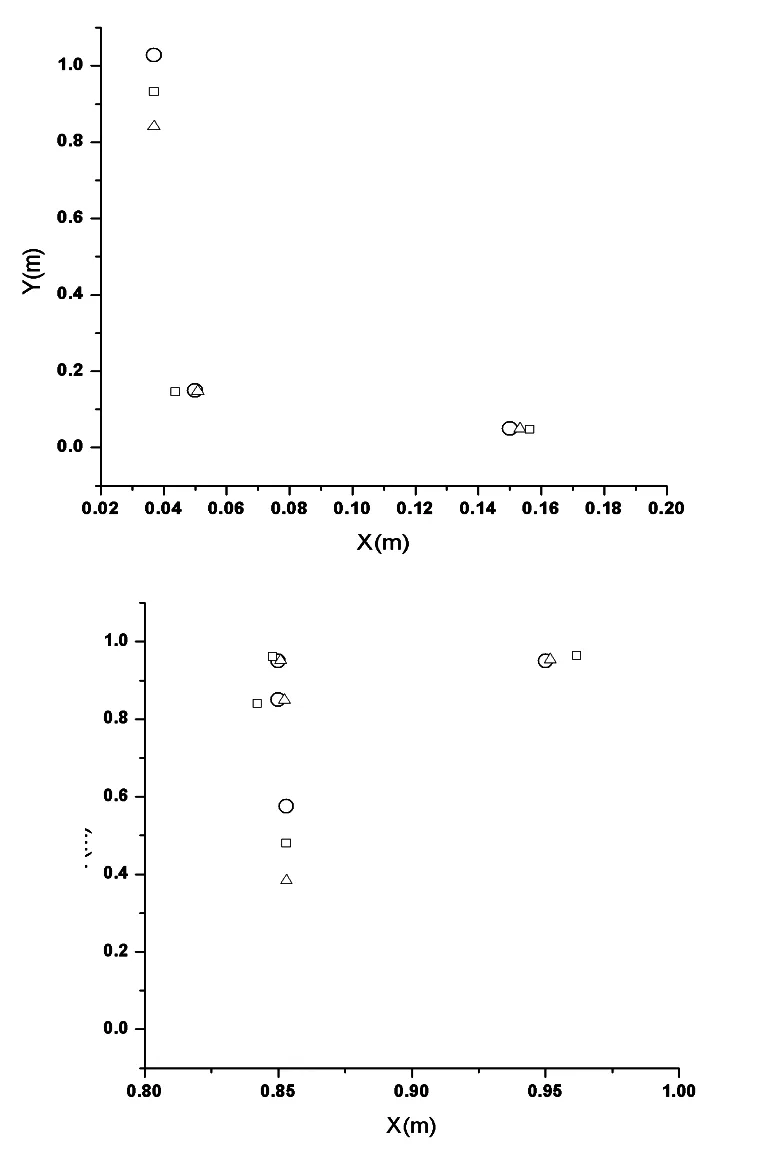
图10 定位误差修复算法效果图

95%的测试点实现了1 cm以内的定位误差，其余的测试点均实现了2 cm以内的定位误差；系统的二维定位平均定位误差为0.87 cm。具体的二维定位误差分布在图8中展示，可以清晰地看出，在模型的边缘处定位误差较大，这是由于在模型边缘处，光信号的幅度受到漫反射物体的影响较大，对人工神经网络的非线性拟合能力要求更大；另一种可能的解释是在模型的边缘区域，来自远离该区域的LED光信号较弱，受到的噪声影响更大。为此可通过增加隐藏层的节点数目或者上述的误差修复算法对边缘区域的误差进行进一步消除。

对误差超过1 cm的5个测试点采用误差修复算法进一步逼近后，定位误差的修复效果如图10所示。

3.2.3 三维定位实验

在完成了神经网络高度信息训练后，使用三维路径测试实验对系统的三维定位效果进行测试，测试的高度范围为0.3～0.5 m，以0.1 m为高度分辨率，共3个高度平面，每个高度平面上通过随机抽样的方式选定5个测试点，并且根据抽样的顺序依次连接形成一条随机测试路径，具体的实验结果如图11所示。

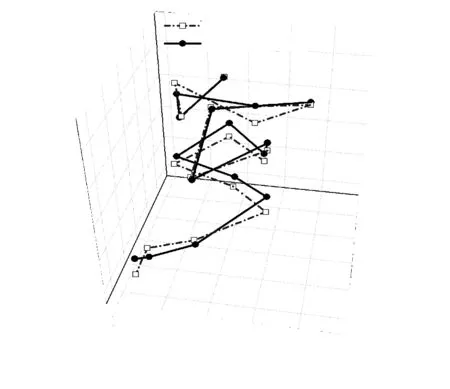
图11 随机路径实验

图12所示的三维定位误差分布直方图，在参与测试的15个测试点中，4个点实现了1 cm内的定位精度，14个点实现了3 cm内的定位精度，随机路径实验的平均定位误差仅为1.47 cm。

如果对所有的测试点采用误差修复算法进一步逼近，得到图13的三维随机路径定位结果。

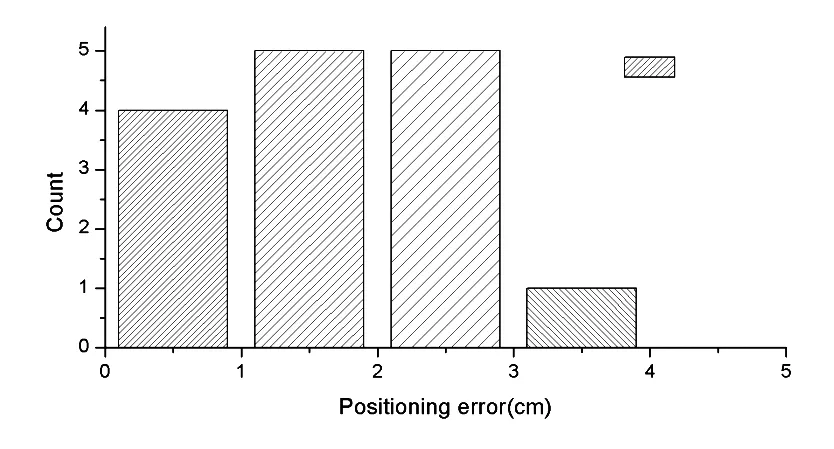
图12 三维定位误差分布直方图

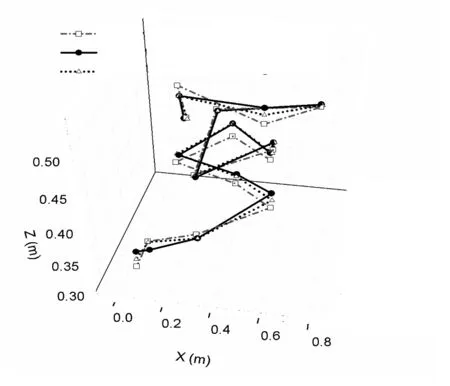
图13 随机路径实验：使用误差修复算法。

Fig.13 Random path experiment: use error repair algorithm.

图14是定位误差修复后的误差分布直方图，可以直观地看出，使用误差修复算法后整体的定位误差可控制在2 cm内。

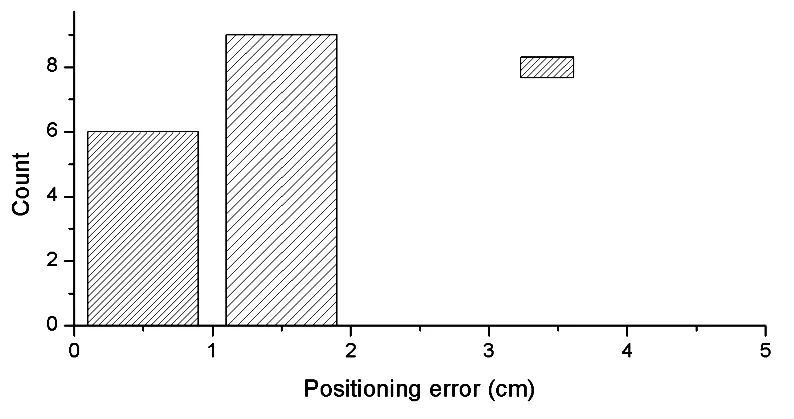
图14 使用误差修复算法后的随机路径定位误差

Fig.14 Random path positioning error after using error repair algorithm

4 结 论

本文提出了一种基于接收信号强度的室内可见光通信定位系统，包括硬件设计及算法设计。在硬件设计上充分考虑了真实应用场景，采用CDMA技术解决参考点通信干扰问题，由于室内漫反射信道的解析表达式复杂，故采用神经网络学习的方式拟合室内的真实信道参数；而针对随机过程带来的定位误差，提出一种定位解迭代逼近算法，进一步减小定位误差。实验结果表明：未使用逼近算法的前提下，本系统在用于二维定位时，99%以上的测试点实现了1 cm以内的定位误差，平均定位误差仅为0.87 cm；本系统在用于三维定位时93%的测试点实现了3 cm以内的定位误差，平均定位误差为1.47 cm；而使用逼近算法后，二维定位测试点的误差可控制在1 cm内，三维定位测试点的误差可控制在2 cm内。