基于Matlab的下荆江二元岸坡崩塌过程动态模拟

2019-01-18陶桂兰吴俊东

水道港口 2018年6期

陈洁，陶桂兰，吴俊东

(1.河海大学港口海岸与近海工程学院，南京 210098；2.长江勘测规划设计研究有限责任公司，武汉 430010)

下荆江河段多为上粘下砂二元结构岸坡，且粘土层较薄，高水期下部砂土层受水流冲刷逐渐掏空、上部粘土层失去支撑后易发生崩塌破坏。特别是2003年三峡水库蓄水运行后，上游来沙量大幅减少，下荆江河段普遍冲刷，局部失稳崩岸屡屡发生[1]，不仅影响堤防安全，也会给航道条件的稳定带来不利影响，进而制约长江中下游“黄金航道”尺度的提升。目前关于二元结构岸坡崩岸机理的研究已取得一定进展：Thorne和Tovey[2]总结了二元结构河岸可能发生剪切、绕轴及拉伸崩塌这3种崩岸形式，针对较为常见的绕轴崩塌给出了相应河岸稳定性计算方法。Fukuoka[3]通过野外试验观察研究，提出采用上部粘土层临界悬空宽度来预报崩塌发生。夏军强[4]结合下荆江河段崩岸特征，改进了粘土层临界悬空宽度及河岸稳定系数的计算公式。

关于河岸稳定性分析模型，目前应用较为广泛的是从经典Osman-Thorne理论[5]发展而来的BSTEM(bank stability and toe erosion model)模型：国外学者曾运用该模型分析了Osage River[6]、Lost Creek[7]和Barry Fork Creek[8]等河流的河岸稳定性问题；国内学者王博[9]、宗全利[10]和张翼等[11]分别应用该模型模拟了长江中游二元河岸的崩退过程。BSTEM模型主要验算岸坡悬臂的剪切崩塌，且在计算坡脚冲刷时假定所有崩塌土体立刻被近岸水流冲走，若要考虑崩塌土体的坡脚掩护，则需对采用该模型得到的崩岸后河岸形态进行人为修正[10-11]，操作较为繁琐。而根据实测资料，下荆江典型二元河岸失稳以绕轴崩塌为主[4]，崩塌土体部分堆积坡脚，在一定时间内掩护近岸河床，BSTEM模型有待改进，需要针对上部粘土层的绕轴崩塌验算岸坡稳定、同时考虑崩塌土体在坡脚堆积的掩护作用建立分析模型。此外，BSTEM模型基于Excel宏命令运行，在时间上是静态的，仅能探究特定情形或固定指标下的河岸稳定性，刘万利、邓姗姗[12-13]研究指出，除近岸水流冲刷这一主要冲积因素外，河岸形态、土体组成及河道水位变化等因素也对崩岸过程有较大影响，建立模型时有必要考虑外部因素(水位升降、土体性质、坡脚冲淤、岸坡形态等)随时间推移的耦合变化使河岸状态发生的改变。

为此，本文针对下荆江河段概化的典型二元结构岸坡，考虑了水位、土体性质、坡脚冲淤、岸坡形态等因素随时间的耦合变化，利用Matlab编程模拟了水位升降过程中的下部砂土层淘刷、上部粘土层绕轴崩塌、以及崩塌土体堆积输移这3个循环阶段[3]，建立了下荆江岸坡崩塌动态分析模型。在此基础上，重点探讨了不同水位变化模式对河岸崩退过程的影响，为二元结构岸坡稳定性及其崩岸规律研究提供参考。

1 岸坡崩塌模型

本文改进现有岸坡崩塌的临界判断条件，推导崩塌土体在坡脚堆积宽度公式，建立起二元岸坡崩塌动态分析模型。该模型以计算水流冲刷导致的岸坡形态改变为基础，针对上部粘土层出露悬臂的绕轴崩塌验算岸坡稳定性，同时考虑崩塌土体在坡脚的堆积掩护与输移，模拟了岸坡崩退过程中循环发生的3个主要阶段。

1.1 岸坡横向冲刷距离的计算

水流对河岸土体的横向冲刷距离ΔB根据剩余切应力法计算[13]

ΔB=K·Δt·(τ0-τc)

(1)

(2)

τ0=γwRJ

(3)

式中：K为土体侵蚀系数，m3/N·s，与土体自身性质有关，本文采用Hanson等[14]提出同时适用于粘性土和砂性土的经验公式计算，见式(2)；Δt为冲刷时间，s；τc为河岸土体起动切应力，N/m2，一般通过土体冲刷试验或根据粒径大小按照经验公式计算得到；τ0为水流切应力，N/m2，与水深成正比；γw为水体容重，N/m3；R为水力半径，m；J为水面比降，m/m。

对于上粘下砂二元结构岸坡，当水流切应力超过下部砂土层的起动切应力后，该土层将逐渐被近岸水流掏空，使得上部粘土层出露悬空，本文根据每个分析时段冲刷后的岸坡断面形态确定粘土层实际悬空宽度。

1.2 岸坡崩塌临界条件的判断

图1 上部粘性土层悬空土块的受力分析Fig.1 Stress analysis of upper cohesive cantilever of composite riverbank

上部粘土层的悬空宽度随水流冲刷逐渐增大，当超过某一临界值时，自身重力矩大于土体抵抗力矩，使其绕某一中性轴产生向河槽方向的旋转运动倒入水中，即绕轴崩塌，如图1所示。

根据悬臂梁平衡原理，当粘性悬空土块处于临界状态时，其自重W引起的外力矩与土体潜在断裂面上产生的抵抗力矩相平衡，即[4]

(4)

式中：Bc为粘土层临界悬空宽度，m；H1、Ht分别为粘土层厚度和其顶部张拉裂隙深度，m；a为粘性土的抗拉、抗压应力之比，即a=σt/σc；σt、σc分别为土体的抗拉、抗压强度，kPa；W为单位长度悬空土块自重，kN。

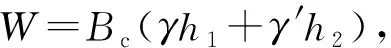
(5)

(6)

式中：h1、h2分别为计算水位以上及以下的粘土层厚度，m，满足h1+h2=H1；γ′为水位以下的粘性土容重，取其浮容重；γ为水位以上的粘性土容重，考虑到粘性土的低渗透性，落水期土体内部水分来不及排出，取其饱和容重；Ht为粘性土顶部张拉裂隙深度，m，本文采用Terzaghi提出的经验公式[15]估算，见式(6)；c、φ分别为粘性土的粘聚力，kPa，摩擦角(°)；其他符号含义同上。根据上部粘土层悬空宽度实际值B与临界值Bc之间的相对关系，可以判断其是否发生绕轴崩塌：若B>Bc，则表示粘性悬空土块崩塌。

1.3 崩塌土体在坡脚堆积宽度的计算

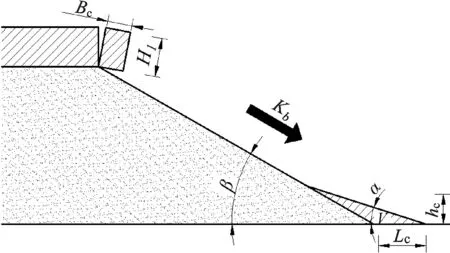
图2 崩塌土体在坡脚堆积掩护示意图Fig.2 Sketch of covering of collapsed soil at bank toe

粘性悬空土块崩塌后将在坡脚堆积掩护，随后在水流作用下逐渐分解并输移，如图2所示，本文仅考虑计算断面崩塌土体在坡脚堆积的掩护作用。

根据下荆江二元河岸崩塌过程的概化水槽试验结果[16]，崩塌土体在坡脚呈三角形堆积，堆积体积占崩塌体积一定比例，堆积坡度近似等于河岸水下稳定坡比或泥沙水下休止角。本文据此确定堆积体积V和堆积坡度α，则崩塌土体在坡脚堆积宽度Lc和堆积高度hc满足关系式

Lc=(cotα-cotβ)hc

(7)

(8)

V=KbBcH1

(9)

式中：Lc、hc分别为崩塌土体堆积的宽度和高度，m；α和β分别为坡脚堆积土体坡度和岸坡坡度，°；V为堆积土体体积，m3；Kb为堆积系数，即堆积土体占崩塌土体的体积比例，可根据水流条件确定：流速越大，水流对土体冲刷作用越强，Kb值越小；Bc、H1分别为崩塌粘土块的宽度和厚度，m。根据式(8)和式(9)求得堆积高度hc，将hc代入式(7)得到崩塌土体在坡脚堆积宽度Lc的计算公式如下

(10)

由于下部砂土层抗冲性较差、易起动，而粘性土受颗粒间粘结力影响具有较大的起动切应力，因此粘性崩塌土体一定时间内的掩护作用使得坡脚抗冲性增强、侧蚀速率减小[16]。本文分析时首先判断上部粘土层崩塌情况，若岸坡发生崩塌，根据式(10)计算崩塌土体堆积宽度Lc，下一时段水流首先冲刷坡脚堆积的粘性土，冲刷距离根据式(1)～式(3)代入粘性土参数求得，待粘性土覆盖层全部被水流冲散输移，水流继续冲刷坡脚砂性土。

2 基于Matlab软件的岸坡崩塌过程模拟

2.1 基于Matlab的岸坡崩塌动态模拟程序

图3 岸坡崩塌模型计算流程Fig.3 Calculation process of bank slope collapse model

Matlab软件是美国MathWorks公司出品的商业数学软件，拥有强大的算法开发、数值计算、数据分析及数据可视化功能，本文采用该软件编制二元岸坡崩退过程的动态模拟程序，计算流程见图3。

由此建立的岸坡崩塌模型具有以下特点：(1)高效的数值计算功能。将计算总时段细分为若干分析时段，利用循环语句模拟水位、土体性质、坡脚冲淤、岸坡形态等因素随时间的耦合变化；(2)动态的图形处理功能。利用动态绘图实现岸坡崩退过程中的断面形态变化展示；(3)便捷的输入输出界面。输入不同初始条件即可应用该程序模拟不同岸坡的崩塌过程，计算结果便于汇总输出，实现与有限元等其他软件的数据交换。

2.2 二元岸坡崩塌模型验证

为了验证岸坡崩塌模型的计算可靠性，本文采用所编写的程序模拟了下荆江荆98断面岸坡[11]在2006～2007水文年内的崩退过程，相关输入参数与现场实测数据见文献[11]，天然河岸水下稳定坡比取为0.323[17]，模拟所得崩后断面与BSTEM模型计算结果以及现场实测数据的对比如图4所示。由图可见，本文模型计算得到的岸顶崩退总宽度(70 m)与实际情况(72 m)较为符合，且模拟的崩后河岸形态与实际形态的差别也相对较小。

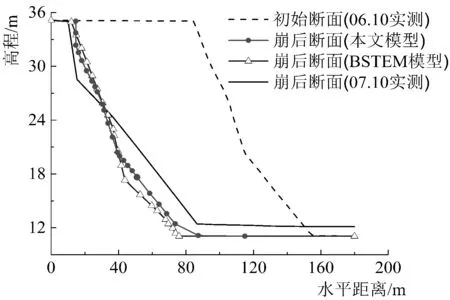
图4 荆98断面岸坡崩后断面计算结果对比Fig.4 Comparison of cross-section after bank collapse at Jing 98

3 下荆江二元岸坡崩岸过程模拟分析

在岸坡崩塌模型验证可靠的基础上，本文应用该模型重点探讨了不同水位变化模式对二元河岸崩退过程、崩塌形态变化及坡脚冲刷距离的影响。

3.1 河段概况及典型断面概化

根据相关地质资料[18]，下荆江两岸主要为河流冲积平原，地势平缓，地形地貌及地质结构相近。因此，本文汇总下荆江(藕池口—城陵矶段)岸坡断面、土体参数等数据，按各河段长度加权计算其平均值作为概化岸坡参数，以使研究对象更具普遍性与代表性，岸坡土体参数见表1。二元河岸的岸坡形态与上部粘土层厚度有重要关系：当粘土层较薄时，岸坡坡度上陡下缓，本文将粘土层坡度简化为垂直，概化岸坡断面如图5所示。

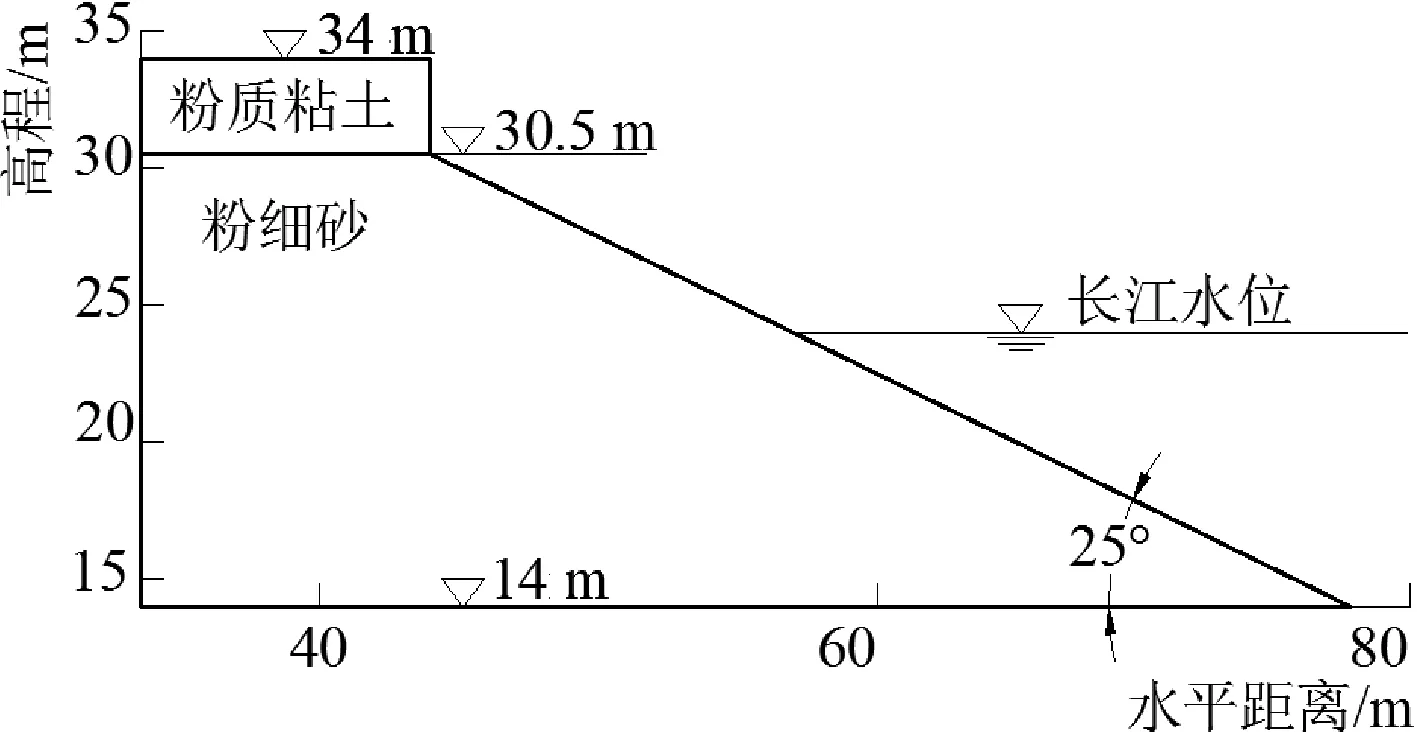
图5 二元结构概化岸坡断面Fig.5 Generalized cross-section of composite river banks

土体参数天然容重/kPa含水率/%孔隙比粘聚力/kPa内摩擦角/°粘性土18.6320.9221.911砂性土20.2220.58028.8

3.2 计算参数与模拟工况

影响岸坡冲刷的因素主要有土体侵蚀系数、起动切应力、水力半径和水面比降等。水力半径R近似为岸坡水深；水面比降J根据岸坡断面上、下游水位差求得，涨水期取0.008、落水期取0.012。土体参数取值如表2所示[18]。

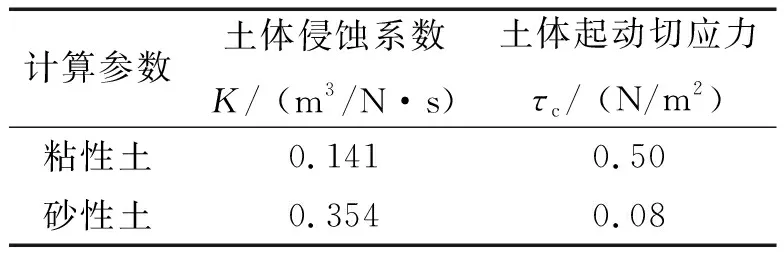
表2 土体计算参数[18]Tab.2 Soil calculation parameters[18]

表3 水位变化模式Tab.3 Modes of water level variation

影响粘土层崩塌的因素主要有粘性土的粘聚力、摩擦角、容重和抗拉强度，前三者取值见表1。粘性土抗拉强度σt可根据其抗剪强度估算得到，并随含水率增加呈先增加后减小的规律[4]，高、低水位下分别将其取为4 kPa和7 kPa。根据下荆江河岸崩塌概化试验[16]，高、低水期分别取崩塌土体堆积系数Kb为0.27和0.58，取其水下堆积坡比tanα=1/2.5。长江监利站2012～2014年的水位资料表明[19]，长江水位最高、最低值分别为34 m和24 m左右，涨水速率和退水速率相近，约为0.1 m/d。据此，本文选取计算工况如表3所示。

3.3 二元结构岸坡崩退过程模拟

两种水位变化模式下，二元结构岸坡崩退形态变化如图6、图7所示，其中带五角星符号的断面线代表两工况的第一次崩后形态，其余带相同符号的断面线分别对应于相近冲刷时长后的岸坡形态，矩形框内为坡脚的局部放大图。

对于处于水位下降模式的工况1，水位下降初期岸坡受水流冲刷的范围较广且冲刷量较大，上部粘土层悬空、不断发生绕轴崩塌。随着水位继续下降，岸坡横向冲刷范围及冲刷量均随之减小，高程大的岸坡点逐渐露出水面不受冲刷，上部粘土层保持稳定不再崩塌。对于处于水位上升模式的工况2，其岸坡崩退形态的变化规律与工况1恰好相反：随着水位逐步上升，岸坡横向冲刷范围及冲刷量均由小变大，高程大的岸坡点逐渐开始受水流冲刷，上部粘土层进入悬空状态发生绕轴崩塌。两工况下岸坡的具体崩塌情况汇总如表4所示。

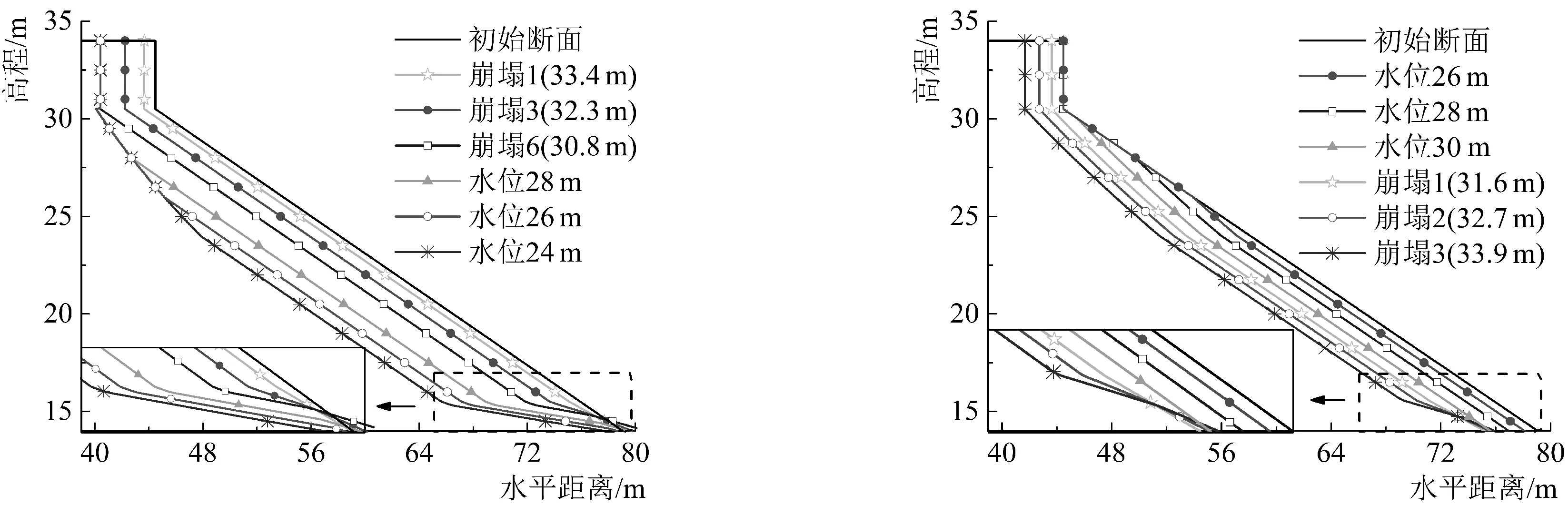
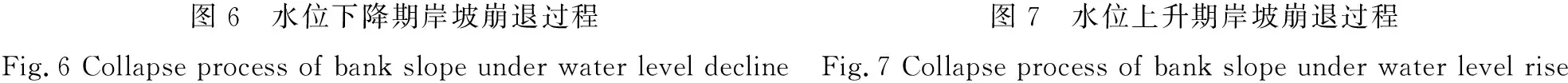
图6 水位下降期岸坡崩退过程Fig.6 Collapse process of bank slope under water level decline图7 水位上升期岸坡崩退过程Fig.7 Collapse process of bank slope under water level rise

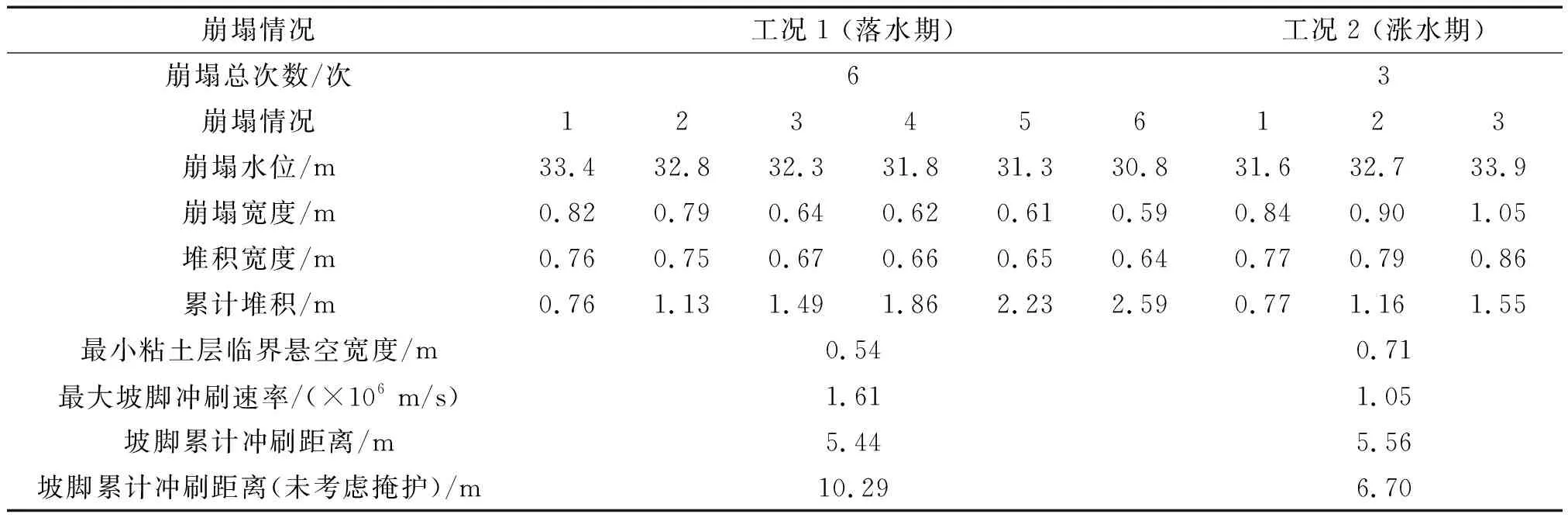
表4 两种水位变化模式下岸坡崩塌情况Tab.4 Slope collapse under two modes of water level variation

结合表4和图6、图7中两工况的最终崩后断面对比可见，水位下降过程中岸坡的崩塌总次数、崩退总宽度均大于水位上升过程，其主要原因和岸坡冲刷幅度与土体性质有关：一方面，水位下降前高水位对河岸土体的浸泡降低了其抗拉强度、土体断裂面产生的抵抗力矩较小；另一方面，相同水位下，水位下降期较大的水面比降[18]使得其岸坡冲刷速率略大于水位上升期，由此导致该时期的粘土层实际悬空宽度较大，同时由于粘性土的低渗透性，土体内部水分来不及排出，饱和悬空土块产生的自重力矩较大。综上，较小的有利抵抗力矩与较大的不利自重力矩，使得水位下降模式下岸坡上部粘土层更易发生绕轴崩塌。

根据式(3)，岸坡冲刷速率与水位成正比，由此水位下降初期粘土层的实际悬空宽度累加最快，但高水位时的水体浮托力有利于其稳定性；随着水位下降，粘土层临界悬空宽度随浮托力的逐渐消失而减小，较大的岸坡冲刷速率使得其实际悬空宽度仍较快累加，最终导致水位变化至两土层交界面附近时(33～31m)最易发生绕轴崩塌。同理对于涨水期，中高水位时(31～33 m)粘性土悬空宽度较大的实际值与较小的临界值使其成为崩岸的最危险时期。

虽然水位下降期的坡脚冲刷速率稍大于水位上升期，但两工况下的坡脚最终累计冲刷距离相近，分别达5.44 m和5.56 m，这与崩塌土体的掩护作用有关：工况1在水位下降初期(33.4 m)就发生上部粘土层绕轴崩塌，崩塌土体堆积掩护，减缓坡脚冲刷速率。随后不断发生岸坡崩塌、崩塌土体堆积，水流持续以较小速率冲刷坡脚粘性土。粘性土掩护层在水位下降末期(24.7 m)被完全冲散，水流重新以较大速率冲刷坡脚砂性土；而工况2在水位上升中后期(31.6 m)才开始发生岸坡崩塌、受崩塌土体掩护的影响减缓坡脚冲刷速率，由此导致其最终累计冲刷距离接近工况1。与未考虑坡脚掩护相比，落、涨水期的坡脚累计冲刷距离分别减少约45%和17%，说明崩塌土体堆积坡脚的掩护作用一定程度上影响了岸坡崩退过程，崩塌次数越多、影响程度越大。