基于copula的失效模式相关的系统可靠度研究
2019-01-18郭亚洲张淑华
郭亚洲, 张淑华
(河海大学 港口海岸与近海工程学院,南京 210098)
系统可靠度计算一直存在瓶颈,就是如何找出复杂系统的失效模式,并在考虑元器件间、各失效模式间的相关性下计算系统的可靠度。在可靠度意义上,系统可以看作是多个可能的失效模式组成的串联系统,各失效模式间所包含的随机变量至少是部分重合的,因此各失效模式间具有相关性。失效模式间的相关性介于完全相关和相互独立两种极端假定之间,它们之间相关性的度量是可靠度分析时的一大难点,以往一般采取的独立假定虽然大大简化了计算,但结果偏于危险。目前考虑变量间、失效模式间相关性的方法主要有二阶界限法[1],相关系数大于0.6时,界限范围较大,精度较低;Nataf变换法[2]将非正态变量转换为正态变量,通过求解多维正态积分计算可靠度,方法简便但计算困难。Rosenblatt变换法[3],将相关变量转换为独立变量,但需获知精确的联合概率分布函数,很难应用于实际工程中;简化多维积分计算的降维分解法[4-6]:结果精确度足够,适用于极限状态方程易于分解的;近似计算法:PNET法(概率网络估算法)[7],可以识别出代表失效模式,并用其计算系统可靠度,减少计算量且精度较高。Monte-Carlo方法[8]及其改进是精确方法,能计算任何系统的可靠度,对于大型复杂系统工作量过大,常作为检验新方法的标准解。这些理论大多建立在线性相关系数ρ基础上,存在以下缺陷:只能描述线性相关关系,无法描述非线性的相关关系,例如x和x2之间的关系;ρ的计算受联合概率密度函数及相关元个数影响较大,对于概率密度函数较为复杂或存在多个相关元的结构,ρ的求解较为困难;ρ通常用于描述正态变量之间的相关性,非正态变量需要先转换为正态变量,局限性较大。因此本文提出了一个基于copula的考虑失效模式间相关性的系统可靠度分析方法,可以更精确地解决工程可靠度问题。copula方法是近年发展起来的方法,目前主要应用于水文、金融和结构工程等领域[9-12],由于其在处理变量之间相关性方面的独特优势,逐步被引入到可靠性领域,唐小松等[13]基于二维 Copula 函数构建了变量的联合分布函数,采用直接积分对结构进行了可靠度分析;Tang 等[14]研究了不同二维 Copula函数构建的二维变量相关模型的差异,分析了其对可靠性分析结果的影响;Jiang等[15]基于Vine Copula函数构建了多维可靠性分析模型,为多维相关性的结构可靠性问题提出了一个新的解决途径。以上是copula在可靠性方面应用的初步探索,有待进一步发展。Copula函数在处理相关性方面有如下优势:copula函数可以将随机变量联合分布的构建拆分为边缘分布形式的估计和边缘分布之间的相关结构两个部分,使联合分布的构建更为方便;copula函数能够描述边缘分布为非正态分布的变量间的相关性;copula能描述变量之间的非线性相关甚至尾部相关。本文的方法为非正态变量之间的线性相关关系的描述提供了一种新的途径。
1 copula计算模型
1.1 copula理论
Copula函数是联合分布与边缘分布之间的连接函数,本质上它也是一种联合分布函数。已知n维随机变量X=(X1,X2,…,Xn);由Sklar[16]定理,存在函数C使得任意分布的边缘分布如:F1(X1),…,Fn(Xn)的联合分布函数F表示为
F(X1,X2,…,Xn)=C(F1(X1),F2(X2),…,Fn(Xn))
(1)
那么随机变量X的联合概率密度函数为
(2)
式中:c为copula函数C的密度函数,所以c的表达式为
(3)
Copula函数通常使用Kendall秩相关系数τ或Spearman秩相关系数ρ作为相关性测度,它们与copula的相关系数θ(用以表示相关性)关系如下
(4)
1.2 常规的copula函数
现有的copula应用大多针对二维问题,表1中列举了几种常见的copula函数。

表1 常见的copula函数Tab.1 Common copula function
1.3 系统可靠度的copula计算模型
本文copula计算模型的构建主要分为两步:一是copula的选择,二是模型的构建。
1.3.1 copula选择
本文采用基于非参数核密度估计的copula选择原理[17],其核心思想是采用非参数核密度估计样本边缘分布,从待选copula函数中初步筛选出能描述失效模式间相关性的copula函数,同时采用copulafit函数估计copula中的相关参数,最终通过比较几种copula与经验copula[18]的欧氏平方距离选出最优copula。
1.3.2 计算模型构建

(5)
式中:ui=FXi(i=1,2,…,n);u=(u1,u2,…,un)。
根据式(6)在边缘分布已知情况下,可以选择合适的copula函数构造联合分布函数。设系统有k个不同的失效模式,其相应的功能函数为
Yj=zj(X1,X2,…,Xn)j=1,2,…,k
(6)
则Ej=[zj(X1,X2,…,Xn)≤0]表示第j个失效模式出现,系统的失效概率表示为
(7)
结构系统主要分为两类:串联系统(只要任意一个极限状态失效,则认为系统失效)和并联系统(所有极限状态全部失效,则认为系统失效),结合copula理论推导出相应的系统可靠度计算模型。
(1)串联系统。
系统失效概率为
(8)
(2)并联系统。
系统失效概率为
(9)

注:基准面采用黄海平均海平面。图1 秦皇岛某直立堤断面示意Fig.1 Cross section of the vertical breakwater at Qinhuangdao port
2 防波堤可靠度分析
2.1 防波堤概况
本文的实例计算采用的是秦皇岛某防波堤[19]。此防波堤形式为沉箱式直立堤,沉箱以及上部结构的材料全部采用钢筋混凝土,沉箱内填充块石。防波堤总长为250 m,每个沉箱纵向长度为12.5 m,共分为6个舱格,防波堤各部分高程详见图1。
2.2 失效概率计算


表2 荷载统计参数Tab.2 Statistic parameters of the loads
表2中P和Pu分别代表水平波浪力和浮托力,Mp、Mpu为其相应的力矩,此外重力G和摩擦系数f为定值,参考文献[22]中的数值,G取945.46 kN·m-1,f取0.6,重力的力矩MG计算得5 923.59 kN·m·m-1。
本文选取的是较常见的滑动(Z1)、倾覆破坏状态(Z2),另一种滑移破坏状态(Z3)失效概率过小,对系统可靠度影响较小,可以忽略[21]。所以文中列出的两种代表性的失效模式完全可以代表全部失效模式,并用其求解系统失效概率,其极限状态方程如下
Z1=g(G,P,PU,f)=(G-PU)·f-P=0
(10)
Z2=MG-MP-MPU=0
(11)
Z3=(G+G1)·f2-P(地基为砂)Z3=Su·l1-P(地基为饱和粘性土)
(12)
式中:重力G1为擦破裂面所围的抛石的重力;系数f2为抛石基床与天然地基的摩擦系数;Su为地基土的粘聚力;l1为基床滑裂段的长度。
本文采用蒙特卡罗数值模拟(Monte Carlo Simulations, MCS)方法[22]计算每个失效模式的失效概率。MCS 方法计算结构失效概率时,主要分两步:一根据各随机变量分布形式产生随机数,二将其代入极限状态方程得到相应失效模式的失效概率。G和f看作定值,水平波浪力和波浪浮托力均采用Gumbel 分布,其分布形式为
F(x)=exp{-exp[-α(x-β)}
(13)

根据随机变量的分布形式(13)采用MATLAB编程产生随机数,带入极限状态方程,得出滑移失效模式以及倾覆失效模式的失效概率,并与以往文献[23]的计算结果进行对比,验证本文所得结果的正确性,详见表3。

表3 失效概率计算结果Tab.3 Calculation results of failure probability
由表中数据看,本文失效概率计算结果误差在允许范围内,满足工程精度要求,可以应用于求解系统失效概率。
2.3 失效相关的系统可靠度计算
2.3.1 确定边缘分布
令X、Y分别代表滑移失效和倾覆失效的功能函数,X、Y的样本是由上面蒙特卡洛模拟产生的随机数带入功能函数所得。用样条差值法求得X、Y的经验分布,将其与采用核密度估计法得到的核分布估计形式进行对比,见图2、图3。


图2 滑移失效功能函数分布Fig.2 Distribution of slip failure function图3 倾覆失效功能函数分布Fig.3 Distribution of overturn failure function
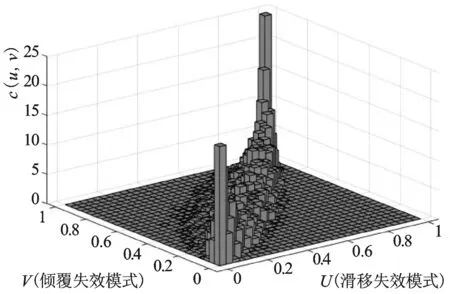
图4 二元频率直方图Fig.4 Bivariate frequency histogram
由图2和图3可知:样本的经验分布和核分布估计图像几乎重合,差别较小,所以经验分布和核分布估计形式都可以作为样本的边缘分布,令U=F(X)和V=F(Y)分别代表X和Y的分布形式。
2.3.2 选取适当的copula函数
根据(Ui,Vi)(i=1,2,…n)绘制二元频率直方图,观察其形状和特征,初步从表1中列举的copula函数中选择符合的copula函数,详见图4。
由图中可得,尾部基本上对称,由表1中所列各copula函数的尾部特性可知,二元正态copula和二元Frank-copula适合于尾部对称且渐进独立;二元t-copula 适合于尾部对称且相关,所以根据图像初步选择二元正态copula或二元t-copula 来拟合之间的相关结构。
2.3.3 参数估计
基于X和Y的样本数据,本文采用MATLAB自带函数copulafit分别确定二元正态copula和二元t-copula 的相关参数。
二元正态copula中的相关参数ρ的估计值为
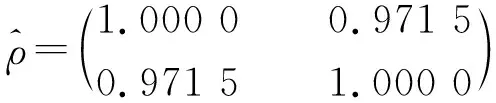
二元t-copula中的相关参数ρ和自由度k的估计值为

二元正态copula的表达式为
(14)
二元t-copula的表达式为
(15)
将二元正态copula和二元t-copula的相关参数分别带入式(14)、(15),计算得出二元正态copula和t-copula 的密度函数和分布函数值,绘制密度函数和分布函数图,见图5~图8。
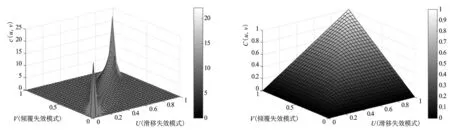
图5 二元正态copula密度函数图Fig.5 Density function graph of bivariate normal-copula图6 二元正态copula分布函数图Fig.6 Distribution function graph of bivariate normal-copula
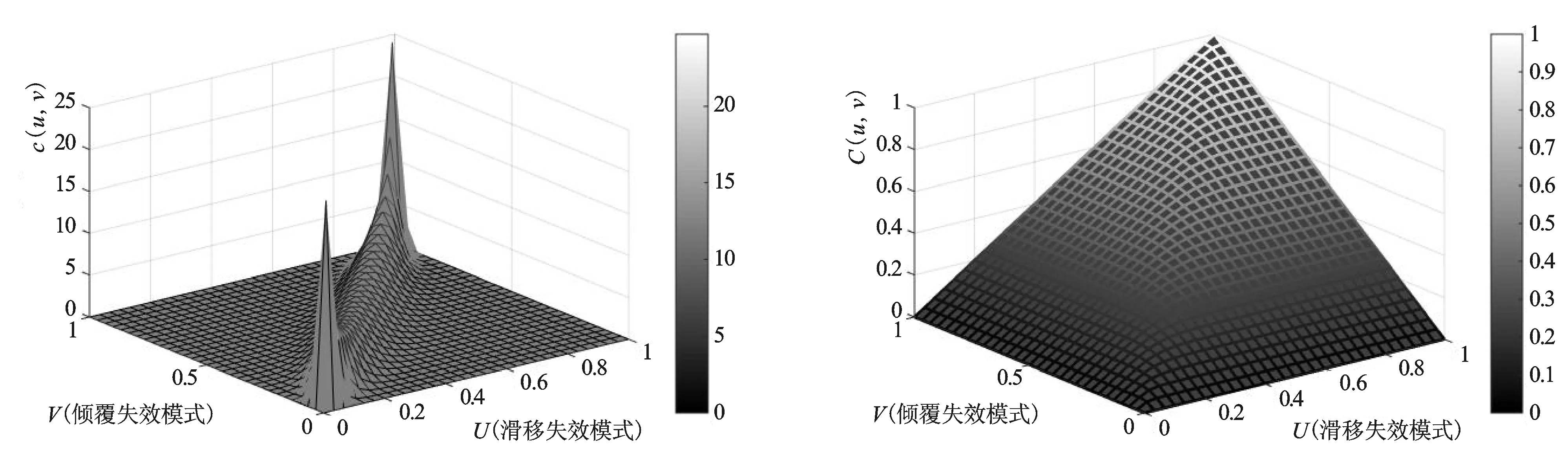

图7 二元t-copula密度函数图Fig.7 Density function graph of bivariate t-copula图8 二元t-copula分布函数图Fig.8 Distribution function graph of bivariate t-copula
由图可得:二元正态copula和二元t-copula对X与Y之间相关结构的拟合程度都比较理想,二元t-copula尖尾特性明显,但由于二者之间差距较小,所以需要进一步通过与经验copula之间的欧氏平方距离筛选出最优copula。
2.3.4 模型评价
计算二元正态copula、t-copula 与经验copula之间的欧氏平方距离,距离最小的为最优copula。记X和Y的经验分布函数分别为Fn(x)和Gn(y),所以定义样本的经验copula为
(16)
式中:I[ ]为示性函数(当Fn(xi)≤u时,I[Fn(xi)≤u]=1;否则I[Fn(xi)≤u]=0)。
则二元正态copula和二元t-copula和经验copula之间的欧氏平方距离分别为
(17)
由表4可知,二元正态copula的欧氏平方距离更小,对于X,Y之间相关结构的拟合更为理想,所以最终选取二元正态copula拟合X,Y之间的相关结构。
2.3.5 系统失效概率
将表3中求解出的X和Y的失效概率和正态copula中的相关参数带入式(9)和(15)中得系统失效概率Pf,并与采用蒙特卡洛模拟[23]求得的系统失效概率进行对比,结果见表5。

表4 欧氏平方距离计算结果Tab.4 Calculation results of Squared Euclidean distance

表5 系统可靠度计算结果对比Tab.5 Comparison of system reliability calculation results
由表5可知:本文构建的基于copula的系统可靠度计算模型所得结果在误差允许范围内,满足工程精度要求。
3 结论
本文基于copula函数,提出了一种结构系统内失效模式相关的结构体系可靠度的计算方法,克服了传统求解结构体系可靠度将失效模式相互独立假设的局限性,为结构体系可靠度的求解提供了一种新思路。以秦皇岛某防波堤为例计算了结构可靠度并与Monte Carlo方法计算结果进行对了对比,验证了本文理论的实用性与结果的正确性。
