基于Sugeno积分形式的犹豫模糊多属性决策方法
2019-01-18谢加良陈水利
岳 娜 , 谢加良*, 陈水利
(1. 集美大学 理学院, 福建 厦门 361021; 2. 集美大学诚毅学院 科研促进部, 福建 厦门 361021)
基于非可加测度的非线性积分由于其柔性表达和非线性融合能力,广泛应用于多属性决策、分类技术、模式识别等领域[1-5].以非线性积分为集成函数的多属性决策方法不仅可以考虑决策属性间的相对重要性,而且可以灵活地描述和处理决策属性间的交互作用.基于此,许多学者针对模糊集、区间模糊集、直觉模糊集等不同的不确定决策信息背景,提出相应的非线性积分算子,并成功应用到多属性决策中[6-11].
在多属性决策实际问题中,决策者对备选方案的评价在几个值之间犹豫不决,传统的模糊集在描述这些不确定信息时表现出局限性,Torra[12]提出犹豫模糊集(HFSs),允许决策者灵活地给出多个可能值,较好解决多准则决策中专家的犹豫不决及多个决策者难以达成一致意见的问题.犹豫模糊集作为一种新的不确定性决策信息描述工具,其理论及其在决策中的应用引起了国内外学者的广泛关注.Xu等[13-14]给出犹豫模糊集的数学形式,研究了犹豫模糊集成算子、相似度测度、犹豫模糊距离、犹豫模糊熵和交叉熵.Wang等[15]提出一种新的犹豫模糊几何算子,并将其应用于多属性群决策中.Wei[16]提出了犹豫模糊优先集结算子,并将其应用于多属性决策中.Xu等[17]提出基于TOPSIS的犹豫模糊多属性决策方法解决具有不完全权重信息的决策问题.然而,以上关于犹豫模糊信息的多属性决策研究多数是建立在属性权重相互独立、互不影响、互不交叉的假设前提之上,而在实际决策过程中属性间却是相互关联、相互作用.
沿用非线性积分解决此问题的独特优势,本文提出基于Sugeno积分形式的犹豫模糊多属性决策方法.通过定义基于Sugeno积分形式的犹豫模糊算子,讨论并证明其幂等性、单调性、有界性和可交换性等集成性质;给出基于Sugeno积分形式的犹豫模糊多属性决策方法,并实例验证在多属性决策实际问题中的应用.
1 基本知识
下面主要介绍犹豫模糊集的基本概念、运算法则、非可加测度、λ-测度等与本文相关的基本概念.
定义1.1[12-13]设论域U={u1,u2,…,un}是一非空有限集合,称
E={〈u,hE(u)〉|u∈U}
为犹豫模糊集,其中hE(u)⊆[0,1]是元素u∈U隶属于集合E的所有可能隶属度构成的集合.为了简便,称h=hE(u)为犹豫模糊元.
定义1.2[13,18]设h1、h2为论域U上任意的2个犹豫模糊元,λ>0,则h1、h2的运算法则规定如下:


定义1.3[13]设论域U是一非空有限集合,h、h1、h2为论域U上的犹豫模糊元,则称
(1)
为犹豫模糊元h的得分函数,其中l(h)为犹豫模糊元h中所含元素的个数.若s(h1) 定义1.4[19]若非空有限集合U上的集函数g:P(U)→[0,1]满足下列条件: 1) 边界条件:g()=0,g(U)=1; 2) 单调性约束:若S,T⊂U,则 S⊂T⟹g(S)≤g(T); 则称g为非可加测度. 定义1.5[3]设λ∈(-1,∞),称非空有限集合U上的集函数gλ:P(U)→[0,1]为λ-测度,如果gλ(U)=1,且对于任意2个不交子集S、T,有 gλ(S∪T)=gλ(S)+gλ(T)+λgλ(S)gλ(T). 显然,λ-测度gλ为非空有限集合U上的非可加测度. 命题1.1[1-2]设U={u1,u2,…,un},gλ是非空有限集合U上的λ-测度.若λ≠0,则对于任意的集合E⊂U,其测度值为 (2) 由λ-测度的定义,可以根据 求得λ的值. 下面利用非可加测度理论定义基于Sugeno积分形式的犹豫模糊算子,讨论并证明其幂等性、单调性、有界性和可交换性等集成性质. 定义2.1设g为非空有限集合U={u1,u2,…,un}上的非可加测度,hi(i=1,2,…,n)为U上的任一组犹豫模糊元,则称 (4) 为基于Sugeno积分形式的犹豫模糊算子,记为HFSL(h1,h2,…,hn),其中,(·)为论域U上的置换,使得h(1)≤h(2)≤…≤h(n),U(i)={u(i),u(i+1),…,u(n)}. 注1显然,如果不考虑属性间的交互作用时,基于Sugeno积分形式的犹豫模糊算子即为文献[13]提出的犹豫模糊有序加权平均算子(HFOWA算子). 由定义2.1易得以下命题. 命题2.1设g为非空有限集合U={u1,u2,…,un}上的非可加测度,hi(i=1,2,…,n)为U上的任一组犹豫模糊元,则 HFSL(h1,h2,…,hn)= (5) 证明由定义2.1可得 故 HFSL(h1,h2,…,hn)= 显然,由(4)式集成的结果HFSL(h1,h2,…,hn)仍为犹豫模糊元. 事实上,令 由于 则 故 0≤γ=1-(1-γ)≤ 从而由(4)式集成的结果HFSL(h1,h2,…,hn)仍为犹豫模糊元. 下面讨论基于Sugeno积分形式的犹豫模糊算子的集成性质. 性质1(幂等性) 设h、hi(i=1,2,…,n)为非空有限集合U={u1,u2,…,un}上的犹豫模糊元.若h=hi(i=1,2,…,n),则有 HFSL(h1,h2,…,hn)=h. 证明由于h=hi(i=1,2,…,n),则 h=h(i),i=1,2,…,n, HFSL(h1,h2,…,hn)= 即 HFSL(h1,h2,…,hn)=h. 再由(5)式,可得 性质3(有界性) 设hi={γi|γi∈hi}(i=1,2,…,n)为非空有限集合U={u1,u2,…,un}上任一组犹豫模糊元,令 则 s≤HFSL(h1,h2,…,hn)≤t. 证明由于 则由(5)式得 s≤HFSL(h1,h2,…,hn)≤t. Step1给出犹豫模糊决策矩阵H=(hij)m×n.对于具有n个属性的决策问题,除空集和全集的测度值分别为0和1外,进一步对其余2n-2个属性子集的测度值进行赋值.本文采用λ-测度进行赋值. Step2根据(3)式确定λ的值,由(2)式计算属性集U上任意属性子集的λ-测度值. Step3构建犹豫模糊得分矩阵,根据得分值分别对每个方案中的属性进行排序. Step4利用基于Sugeno积分形式的犹豫模糊算子集成犹豫模糊矩阵信息,得到各个方案的综合评价值. Step5利用得分函数对每个方案的综合评价值进行排序,从而选出最优方案. 某工厂需要购买一种设备,现有5家供应商Xi(i=1,2,…,5)可供选择,该工厂的决策者将根据U1:产品价格,U2:产品质量,U3:产品售后服务水平,U4:供应商信誉这4种属性对上述5家供应商进行评价,选出最优供应商,其中各属性的λ-测度值为:gλ({U1})=0.30,gλ({U2})=0.25,gλ({U3})=gλ({U4})=0.20. Step1给出犹豫模糊决策矩阵,见表1. 表 1 犹豫模糊矩阵 Step2根据(2)式计算属性集U上任意属性子 集的λ-测度值,见表2.由(3)式可得λ=0.145 9. 表 2 各个属性子集的gλ值 Step3构建犹豫模糊得分矩阵,见表3.根据得分值分别对每个方案中的属性进行排序. 表 3 犹豫模糊得分矩阵 Step4利用基于Sugeno积分形式的犹豫模糊算子集成犹豫模糊矩阵信息,得到各个方案的综合评价值. Step5利用得分函数对每个方案的综合评价值进行排序,从而选出最优方案. 下面以集成供应商X1的犹豫模糊评价信息为例.由表3可得: U(1)={{U1},{U2},{U4},{U3}}, U(2)={{U2},{U4},{U3}}, U(3)={{U4},{U3}},U(4)={{U3}}; h(1)={0.30,0.50,0.60},h(2)={0.70,0.80}, h(3)={0.70,0.90},h(4)={0.80,0.90}. 由(5)式得 HFSL(h1,h2,h3,h4)= {0.580 0,0.627 2,0.637 7,0.678 5,0.671 5, 0.708 5,0.654 7,0.693 5, 0.702 1,0.735 7,0.729 9,0.760 3,0.604 8, 0.649 3,0.659 1,0.697 5, 0.690 9,0.725 7,0.675 1,0.711 6,0.719 7, 0.751 3,0.745 9,0.774 5}. 由(1)式可得 同理可得 s(X2)=0.594 4,s(X3)=0.573 2, s(X4)=0.628 4, 故 s(X3) 从而最优供应商为X1. 本文在犹豫模糊不确定决策信息背景下,通过构建基于Sugeno积分形式的犹豫模糊算子,给出属性间相互关联、相互作用的多属性决策方法.基于Sugeno积分形式的犹豫模糊算子(在不考虑属性间的交互作用时即为犹豫模糊有序加权平均算子)具有幂等性、单调性、有界性和可交换性等良好的集成性质,可以很好地应用于多属性决策实际问题中.本文所讨论的是在已知犹豫模糊信息的多属性决策方法,对于评价信息不完备、不确定或多种形式混合情况的犹豫模糊信息,将是下一步的研究工作.2 基于Sugeno积分形式的犹豫模糊算子
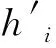


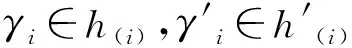


3 基于Sugeno积分形式的犹豫模糊多属性决策方法

4 实例分析
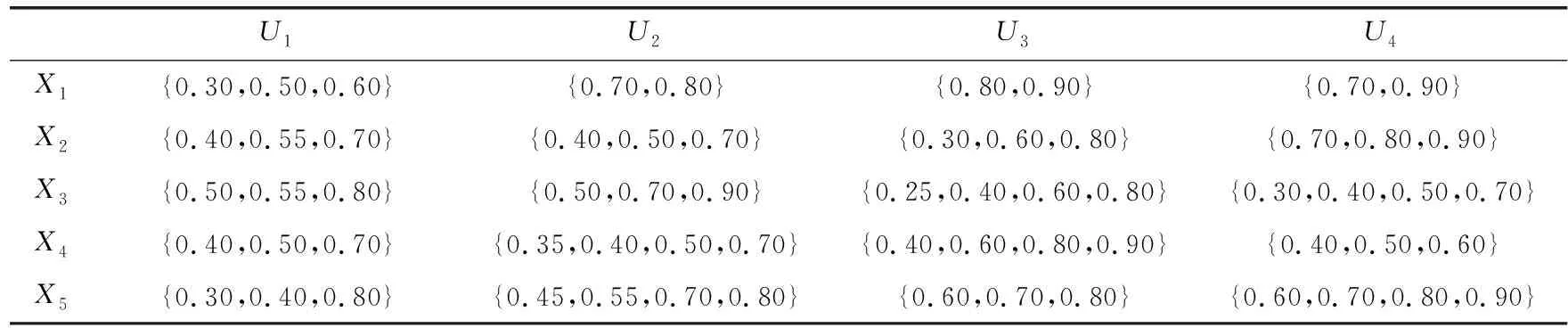

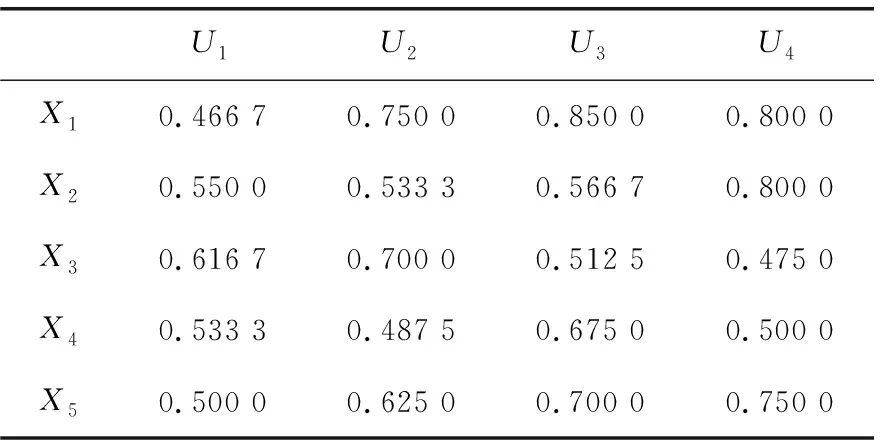
5 结论
