源于非经典逻辑的代数结构研究综述
2019-01-18张小红
张小红
(陕西科技大学 中加数据智能与三支决策研究中心, 陕西 西安 710072)
0 引言
说起逻辑代数,自然要从布尔代数(Boolean algebra)开始.19世纪早期,英国数学家乔治·布尔(George Boole)突发奇想:人的思想能不能用数学表达?此前,数学只用于计算,没有人意识到,数学还能表达人的逻辑思维.为了描述(经典)逻辑命题之间的关系,George Boole于1847年在其著作《The Mathematical Analysis of Logic》中提出一种代数系统,后来被称为布尔代数,从而为数字电子学的发展奠定了重要理论基础,也是现代程序设计语言学、集合论、统计学等的理论基础.最简单的布尔代数是定义在{0,1}上的,其上的二元运算∧、∨及一元运算可分别理解为“取小”、“取大”及“取反”.一般地,一个布尔代数是指代数系统(X;∧,∨,,0,1),其中X为非空集,(X;∧,∨,0,1)是有界分配格,0、1分别是最小元(底元)、最大元(顶元),是X上的补,即满足:
x∧x=0,x∨x=1, ∀x∈X.
(1)
在布尔代数(X;∧,∨,,0,1)上,可自然定义蕴涵运算“→”为
x→y=x∨y, ∀x,y∈X.
(2)
上述蕴涵运算具有如下性质:
x→(y→x)=1, ∀x,y∈X;
(3)
(x→(y→z))→((x→y)→(x→z))=1,
∀x,y,z∈X.
(4)
蕴涵运算与序关系之间有如下紧密联系
x≤y⟺x→y=1, ∀x,y∈X;
(5)
于是,性质(4)可又写成
x→(y→z)≤(x→y)→(x→z),
∀x,y,z∈X.
(6)
在经典数理逻辑中,将逻辑命题用符号表示,命题之间的关系用公理系统刻画,从而建立起经典命题逻辑的语构系统(形式演算系统),它与用“真”、“假”表达命题真值的语义系统是对应的,这是由可靠性定理与完备性定理确立起来的(参见文献[1-3]).
与经典逻辑只有“真”、“假”(即0、1)2个真值不同,多值逻辑、连续值逻辑、模糊逻辑、格值逻辑等非经典逻辑的真值域得到扩大,相应的形式演算系统也逐渐复杂起来,与之相配套的代数系统(本文统称它们为非经典逻辑代数)也比布尔代数广泛得多(当然,它们通常包含布尔代数为其特例).本文将对这些非经典逻辑代数结构进行总结,特别是从蕴涵运算的角度探讨它们之间的内在联系.
1 (可换)剩余格与(伪)t-模基模糊逻辑
就“模糊逻辑”这一术语来说,很难给出一个确切的定义,有多种狭义和广义的不同内涵,本文主要指以[0,1]为真值域的非经典数理逻辑系统.
在数理模糊逻辑理论中,占主导地位的是基于t-模(三角模)的逻辑系统.在这类逻辑演算系统中,使用t-模作为合取联结词的解释,并由此解释其他命题联结词,比如蕴涵、析取联结词分别解释为由t-模诱导的剩余型蕴涵、对偶的t-余模,而否定联结词通常经由蕴涵解释为A=A→0.这样建立的命题演算系统具有许多优良的逻辑性质,反映了人类日常思维与推理中的许多逻辑特征,这类逻辑理论在模糊控制和人工智能研究中已经获得广泛的应用(参见文献[4-9]).
t-模首先出现在Menger于1942年发表的论文“Statistical metrics”(《统计度量》)中.20世纪60年代,Schweizer和Sklar重新严格定义了t-模和统计度量空间(现称为概率度量空间),从而促进了这个领域的飞速发展.由于t-模较好地反映了“逻辑与”的性质,因此t-模作为一般的“模糊与”算子一致受到模糊逻辑学界的青睐.
定义1[5]t-模是满足以下条件的函数
⊗:[0,1]×[0,1]→[0,1],
∀x,y,z∈[0,1]:
1)x⊗(y⊗z)=(x⊗y)⊗z;
2)x≤y⟹x⊗z≤y⊗z,x≤y⟹z⊗x≤z⊗y;
3)x⊗1=1⊗x=x;
4)x⊗y=y⊗x.
定义2[2,7-8]设⊗是[0,1]上的t-模,
R:[0,1]×[0,1]→[0,1]
是[0,1]上的二元函数.如果x⊗y≤z当且仅当
x≤R(y,z), ∀x,y,z∈[0,1],
则称R是与⊗相伴随的蕴涵算子,同时称(⊗,R)为伴随对,此时常记R(x,y)为x→y.
定理1[2,7-8]设⊗是[0,1]上的左连续t-模,在[0,1]上定义→如下:
x→y=sup{a∈[0,1]|a⊗x≤y},
∀x,y∈[0,1],
则→是与⊗相伴随的蕴涵算子.
基于连续t-模,Hájek[4]建立了模糊逻辑形式系统BL;基于R0t-模,王国俊[2-3]建立了模糊逻辑形式系统L*;基于左连续t-模,Esteva等[6]建立了模糊逻辑形式系统MTL.这些模糊逻辑系统的完备性定理均已得到证明,即BL、L*、MTL分别是完全描述连续t-模、R0t-模、左连续t-模基模糊逻辑语义的形式化系统.在证明这些逻辑系统完备性时,相应的代数结构,即BL-代数、R0-代数、MTL-代数,起着重要的作用.而这些代数结构,均是特殊的可换剩余格.剩余格(residuated lattice)的概念最早来自对环的理想格的研究,可参见文献[10-11].
定义3[2,4,10]代数系统(L;∧,∨,→,⊗,0,1)称为是一个可换剩余格(commutative residuated lattice),如果:
(i) (L;∧,∨,0,1)是有界格,这里0、1是最小元、最大元;
(ii) (L;⊗,1)是带单位元1的可换半群;
(iii) 对任意x,y,z∈L,x⊗y≤z⟺x≤y→z.
显然,如果⊗是[0,1]上的一个t-模,→是由⊗诱导的剩余蕴涵,则([0,1];∧,∨,→,⊗,0,1)是一个可换剩余格.
命题1[2,4,10]设(L;⊗,∧,∨,→,0,1)是可换剩余格,则(∀x,y,z∈L):
1) 1→x=x,x→x=1,x⊗0=0;
2)x≤y⟺x→y=1;
3)x⊗(x→y)≤y;
4)x≤y→(x⊗y);
5)x≤y⟹x⊗z≤y⊗z;
6)x→(y→z)=(x⊗y)→z=y→(x→z);
7)x→(y∧z)=(x→y)∧(x→z);
8) (x∨y)→z=(x→z)∧(y→z);
9)x→y≤(z→x)→(z→y);
10)x→y≤(z⊗x)→(z⊗y);
11)x⊗(y∨z)=(x⊗y)∨(x⊗z).
值得注意的是,由t-模诱导的剩余蕴涵,一般不再满足布尔代数中关于蕴涵的性质(2)、(4)及(6)式;同时,若在剩余格中定义“非”运算:x=x→0(∀x∈L),则它不再满足布尔代数中的性质(1)式,与之相对应,在模糊逻辑中“排中律”不再成立.
定义4[4]设(L;∧,∨,⊗,→,0,1)是一个可换剩余格,称L是一个BL-代数,如果满足(∀x,y∈L):
(i)x∧y=x⊗(x→y);
(ii) (x→y)∨(y→x)=1.
定义5[2]设M是(,∨,→)型代数,如果M上有偏序≤使(M;≤)成为有界分配格,∨是关于序≤的上确界运算,是关于序≤的逆序对合对应,且(∀a,b,c∈M):
(M2) 1→a=a,a→a=1;
(M3)b→c≤(a→b)→(a→c);
(M4)a→(b→c)=b→(a→c);
(M5)a→(b∨c)=(a→b)∨(a→c),a→(b∧c)=(a→b)∧(a→c);
(M6) (a→b)∨((a→b)→a∨b)=1.
这里1是(M,≤)中的最大元,则称M为R0-代数.
定义6[6]设(L;∧,∨,⊗,→,0,1)是一个可换剩余格,称L是MTL-代数,如果满足如下的预线性等式
(x→y)∨(y→x)=1, ∀x,y∈L.
定义7[6]设(L;∧,∨,⊗,→,0,1)是一个MTL-代数.L称为是IMTL-代数,如果满足条件
(x→0)→0=x, ∀x∈L.
MTL-代数L称为是WNM-代数,如果满足条件
(x⊗y→0)∨(x∧y→x⊗y)=1, ∀x,y∈L.
MTL-代数L称为是NM-代数,如果它既是IMTL-代数、又是WNM-代数.
定理2[12-13]设(L;∧,∨,⊗,→,0,1)是一个可换剩余格,在L上定义为
x=x→0, ∀x∈L,
则(L;,∨,→)构成R0-代数的充要条件是L满足
x=x,(x→y)∨((x→y)→x∨y)=1,
∀x,y∈L,
即(L;,∨,→)构成R0-代数当且仅当L是NM-代数.
在t-模的定义中,要求其满足交换律,从而在t-模基模糊逻辑系统中“模糊与”算子具有可换性.受非可换逻辑研究的影响(参见文献[14-16]),一些学者开始研究伪t-模(非可换t-模)及基于此的非可换模糊逻辑(参见文献[17-21]),相应的非可换模糊逻辑代数也相继提出.
定义8[17]伪t-模(pseudo-t-norm)是满足以下条件的函数
⊗:[0,1]×[0,1]→[0,1],
∀x,y,z∈[0,1]:
1)x⊗(y⊗z)=(x⊗y)⊗z;
2)x≤y⟹x⊗z≤y⊗z,x≤y⟹z⊗x≤z⊗y;
3)x⊗1=1⊗x=x.

1) (L;∧,∨,0,1)是有界格,其序关系为≤,0、1分别为最小元和最大元;
2) (L; ⊗,1)是幺半群,1为单位元;
3) 对任意x,y,z∈L,


φ1(x,y)=
sup{z|z⊗x≤y};φ2(x,y)=sup{z|x⊗z≤y}.




4)x⊗0=0⊗x=0;







12)x⊗(y∨z)=(x⊗y)∨(x⊗z),(y∨z)⊗x=(y⊗x)∨(z⊗x);




则称L是一个伪MTL-代数(psMTL-代数,又称为弱伪BL-代数).一个MTL-代数L如果还满足条件

则称L是一个伪BL-代数(psBL-代数).
由于前述命题演算系统L*具有良好的应用背景和整齐的结构特性,对其进行非可换拓广是一项很有意义的工作.文献[22]成功地将R0t-模推广到非可换情形,得到第一个具有伪对合性质的伪t-模簇,即伪R0t-模.在此基础上,建立了基于这种伪t-模的非可换逻辑系统PL*,通过引入PL*-代数(它是弱R0-代数、IMTL-代数的非可换推广)的概念,建立了PL*-代数的正规素滤子定理,由此证明了PL*系统的完备性定理.
定理3[8,22]设f1和f2是[0,1]上严格递增连续函数,且f1(1)=f2(1)=1,f1(0)=f2(0)=0.规定
则T(x,y)是一个伪t-模,这里x∧y=min(x,y).
称定理3所给出的伪t-模为伪R0t-模.容易证明,伪R0t-模关于2个变量都是左连续的.如果伪R0t-模中的函数f1和f2均取为恒等函数,即
∀x∈[0,1],f1(x)=f2(x)=x,
则此时伪R0t-模退化为R0t-模.
定理4[8,22]设T是伪R0t-模,则与T相伴的1-剩余蕴涵和2-剩余蕴涵分别为:


(A1) (L;∧,∨,0,1)是有界格,这里0、1分别是最小元、最大元;
(A2) (L;⊗,1)是独异点,即⊗满足结合律且对任意x∈L有x⊗1=1⊗x=x;


(A5)x=x=x;

这里x=x→0,x=x0.
显然,PL*-代数是一种特殊剩余格.关于其他非可换模糊逻辑代数,可参阅文献[23-24].
2 非结合剩余格、一致模及更一般的模糊逻辑系统
在模糊推理与不确定性决策中,非可换、非结合算子具有一定实际应用价值(参见文献[25-28]),因此探讨更一般的“模糊与”(或聚合算子)、相应的蕴涵算子,以及更具一般性的模糊逻辑形式系统,就成为近年来模糊学界的研究热点之一(参见文献[29-38]).
前面提到,将t-模的交换性去掉,引入了伪t-模.类似地,将t-模的结合性去掉,就是非结合t-模[29],也称为可换半t-模[27-28].与非结合模糊逻辑形式系统相对应的代数结构是非结合剩余格,也称为可换剩余格序广群.我们在文献[34-35]中使用“非结合剩余格”这一名称,较国外学者早[29].
定义12[29,34]一个代数结构(L;∧,∨,⊗,→,0,1)称为是一个非结合剩余格,如果L满足条件:
1) (L;∧,∨,0,1)是一个有界格;
2) (L;⊗,1)是一个具有单位元1的可换广群;
3) 对任意x,y,z∈L,x⊗y≤z⟺x≤y→z.
命题3[29,34-35]设(L;∧,∨,⊗,→,0,1)是一个非结合剩余格,则对任意x,y,z∈L有:
1)x≤y⟺x→y=1;
2)x≤y⟹x⊗z≤y⊗z;
3)x≤y⟹y→z≤x→z;
4)x≤y⟹z→x≤z→y;
5)x⊗(y∨z)=(x⊗y)∨(x⊗z);
6)x→(y∧z)=(x→y)∧(x→z);
7) (y∨z)→x=(y→x)∧(z→x);
8) (x→y)⊗x≤x,y;
9) (x→y)→y≥x,y.
下面的例子表明,在非结合剩余格中,如下的蕴涵性质不再成立.注意,由命题1及命题2知,在非可换剩余格中(7)式成立,在可换剩余格中(8)式成立:
y→z≤(x→y)→(x→z), ∀x,y∈L.
(7)
x→(y→z)=y→(x→z), ∀x,y∈L.
(8)
例1设L=[0,1],其上的二元运算⊗定义为
x⊗y=0.5xy+0.5max{0,x+y1},x,y∈L,
则⊗是L上的非结合t-模.蕴涵运算定义为
x→y=max{z∈[0,1]|z⊗x≤y},x,y∈L.
于是(L;max,min,⊗,→,0,1)是一个非结合剩余格.取x=0.6,y=0.3,z=0.1,计算得到:
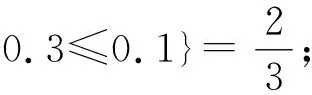


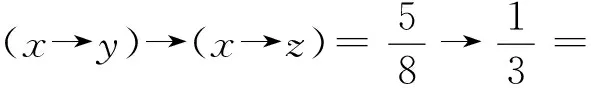
从而
另外,若取,x=0.7,y=0.4,z=0.1,则有
从命题2和命题3可以看出,非可换、非结合模糊逻辑系统都是对t-模基模糊逻辑系统的拓广,但与其相对应的非可换剩余格、非结合剩余格中,序关系≤与蕴涵运算均满足基本t-模基模糊逻辑代数的如下性质
x≤y⟺x→y=1, ∀x,y∈L.
(9)
然而,在研究基于一致模(uninorm)的模糊逻辑系统时,相应的代数结构不再满足这条性质了.2007年,Gabbay等在文献[39]中建立了第一个基于一致模的模糊逻辑系统BUL(与连续一致模相对应).之后,关于一致模及其剩余蕴涵、基于各种一致模或非可换一致模(伪一致模)的模糊逻辑系统相继得到深入研究(参见文献[40-49]).在一致模中,乘法单位元e可以不是最大元1,故由一致模诱导的剩余蕴涵通常不满足条件(9)式.
定义13[39-40]一个一致模*是满足以下条件的一个映射
*:[0,1]2→[0,1], ∀x,y∈[0,1]:
1)x*y=y*x;
2)x*(y*z)=(x*y)*;
3)x≤y⟹x*z≤y*z;
4) 存在e*∈[0,1]使得e*x=x.
如果0*1=0,则称*为合取一致模;如果0*1=1,则称*为析取一致模.
一致模*称为是剩余的,如果存在函数→*:[0,1]2→[0,1]满足
z≤x→*y⟺x*z≤y, ∀x,y,z∈[0,1].
可以证明,一个一致模*是剩余的,当且仅当它是合取左连续一致模,且x→*y=sup{z:x*z≤y}.
定义14[39]一个尖点有界可换剩余格(pointed bounded commutative residuated lattice)是一个代数结构(L;∧,∨,⊗,→,e,f,⊥,┬),其中∧,∨,⊗,→是L上的二元运算,e,f,⊥,┬为常元,且满足:
(i) (L,∧,∨,⊥,┬)为有界格,⊥,┬分别为L的底元和顶元;
(ii) (L,⊗,e)是可换独异点;
(iii)z≤x→y⟺x⊗z≤y,∀x,y,z∈L.
满足以下条件的尖点有界可换剩余格称为UL-代数
e≤((x→y)∧e)∨((y→x)∧e), ∀x,y∈L.
设*是一个剩余一致模,→*是它的剩余,f∈[0,1],则([0,1],min,max,*,→*,e*,f,0,1)是一个UL-代数.
容易验证,在UL-代数中成立,
x≤y⟺e≤x→y,∀x,y∈L,
(10)
e→x=x,∀x∈L.
(11)
前面分别介绍了t-模基模糊逻辑系统的2种推广:一是放弃交换性,得到非可换模糊逻辑系统;一是放弃结合性,得到非结合模糊逻辑系统.自然会想到,同时放弃交换性和结合性,可以得到更一般的模糊系统.确实如此,文献[50-51]就建立了这样的一般模糊逻辑系统,是基于mianorm建立起来的,这里的mianorm是更一般的三角模,与Liu在文献[52]中引入的半一致模(semi-uninorm)涵义相同(早于文献[50]),是文献[53]中提到的t-半模(t-seminorm)概念的推广.
定义15[50,52]一个半一致模(semi-uninorm)或mianorm是指满足以下条件的函数
*:[0,1]2→[0,1], ∀x,y,z∈[0,1],
1) 存在e∈[0,1],e*x=x*e=x,
2)x≤y⟹x*z≤y*z且z*x≤z*y.
当e=1时,半一致模称为半三角模;当e=0时,半一致模称为半三角余模.
对文献[52]中的定理4.1稍加改造,可以得到如下结论:
定理5设函数→:[0,1]2→[0,1]满足以下条件:
1) ∀x,y,z∈[0,1],y≤z⟹x→y≤x→z;
2) ∀x,y,z∈[0,1],y≤z⟹z→x≤z→y;
3) 存在e∈(0,1],使得前述条件(10)及(11)式成立,
则如下定义的运算*1及*2是具有单位e的半一致模:
∀x,y∈[0,1],x*1y=inf{t∈[0,1]:x≤y→t};
∀x,y∈[0,1],x*2y=inf{t∈[0,1]:y≤x→t}.
基于半一致模(semi-uninorm)或mianorm,文献[50]建立了一般模糊逻辑形式系统MIAL,与之配套的代数结构是MIAL-代数.

(i) (L,∧,∨,⊥,┬)为有界格,⊥,┬分别为L的底元和顶元;
(ii) (L,*,t)是有单位t的广群;

一个MIAL-代数是指满足以下条件的尖点有界rlu-广群(∀x,y,z,w∈L):
t≤((x→y)∧t)∨((z*w)→
(z*(w*((y→x)∧t)))),
t≤((x→y)∧t)∨((z*w)→
((z*((y→x)∧t))*w)),
t≤((x→y)∧t)∨(z→
(w→((w*z)*((y→x)∧t)))),

作为更一般与剩余有关的代数结构,称为剩余广群(residuated groupoid),最早可以追溯到1954年Dubreil与Croisot的工作,这在文献[54]中有记载和说明.国内相关研究论文,可参见文献[55-56](注意相关概念的细微差别).按文献[57]的说法,剩余有序广群(residuated ordered groupoid)的概念最早出现在Birkhoff的著作中[58],它是对一般剩余格概念的推广.剩余有序广群也被写为residuated partially-ordered groupoid或residuated pogroupoid(参见文献[59-60]).


如果剩余有序广群L有单位元e,即(∀x∈L)e*x=x*e=x,则称L是有单位的(unital);如果剩余有序广群L有最大元1且它同时是单位元,则称L是整的(integral).


2)x≤y⟹x⊗z≤y⊗z;x≤y⟹z⊗x≤z⊗y;
3) 设xi∈L(i∈I),a∈L.如果∨i∈Ixi存在,则a*(∨i∈Ixi)=∨i∈I(a*xi);
4) 设xi∈L(i∈I),a∈L.如果∨i∈Ixi存在,则(∨i∈Ixi)*a=∨i∈I(xi*a).

1) ∀x,y,z∈L,y→z≤(x→y)→(x→z).
2) ∀x,y,z∈L,x*(y*z)≤(x*y)*z.
类似地,下列条件在L中也等价:

4) ∀x,y,z∈L,(x*y)*z≤x*(y*z).

3 从蕴涵片段看各种模糊逻辑代数
3.1BCK-代数与伪BCK-代数在研究非经典数理逻辑的语构理论时(特别是讨论逻辑系统完备性时),通常要考查与之相关的代数系统的结构特征,比如Lukasiewicz连续值逻辑与MV-代数、形式系统L*与R0-代数、基本逻辑系统BL与BL-代数、非可换基本逻辑psBL与伪BL-代数等,这与经典逻辑与布尔代数的关联关系类似.因此,研究各种源于逻辑的代数系统的内在联系就是一个自然而重要的课题,这将从一个特殊的视角探寻各种逻辑系统深层次的联系.
早在20世纪60年代中期,从正蕴涵演算系统(the systems of positive implicational calculus)、弱正蕴涵演算及BCK系统出发,日本学者Iséki[61]引入BCK-代数的概念.此后,国际学术界对其进行了深入细致的研究,涉及序结构、代数结构、理想(ideal,与滤子概念相对应)、与逻辑的关系等方面[62-72].1984年,日本学者Komori提出BCC(BIK+)-代数的概念,它是BCK-代数的推广.有趣的是,虽然上述研究方向直观上看似乎与模糊逻辑没有关系,然而后来人们发现:它们之间具有密切联系!罗马尼亚学者Iorgulescu首先建立了BCK-代数与模糊逻辑代数系统BL-代数的联系;之后,Iorgulescu及其同行将BCK-代数作了非可换推广,引入伪BCK-代数(pseudo-BCK algebra,简称psBCK-代数),并建立了它们与非可换模糊逻辑代数系统psBL-代数的联系.这些成果表明,各种非经典逻辑在相对应的代数结构方面有着内在的联系,这是进一步认识这些非经典逻辑系统之间关系的新的独特视角.
定义18[61]一个BCK-代数是指代数结构(A;≤,→,1),这里≤是A上的二元关系,→是A上的二元运算,1是A中的一个常元,且满足以下条件(∀x,y,z∈A):
(BCK-1)x→y≤(y→z)→(x→z);
(BCK-2)x≤(x→y)→y;
(BCK-3)x≤x;
(BCK-4)x≤y,y≤x⟹x=y;
(BCK-5)x≤1;
(BCK-6)x≤y⟺x→y=1.
BCK-代数称为有界的,如果存在元素0使得对任意x有0→x=1,即0≤x.
代数结构(A;≤,→,1)若满足前述除(BCK-5)以外的所有其他条件,则称(A;→,1)为BCI-代数.可以验证,BCI-代数中1是极大元,即
∀x∈A, 1≤x⟹x=1.
注1原始文献中BCK(BCI)-代数的定义是上述定义的对偶形式.
定义19[63]一个BCC-代数(或称BIK+-代数)是指代数结构(A;≤,→,1),这里≤是L上的二元关系,→是A上的二元运算,1是A中的一个常元,且满足以下条件(∀x,y,z∈A):
(BCC-1)y→z≤(x→y)→(x→z);
(BCC-2) 1→x=x;
(BCC-3)x≤x;
(BCC-4)x≤y,y≤x⟹x=y;
(BCC-5)x≤1;
(BCC-6)x≤y⟺x→y=1.
注21) 原始文献中BCC-代数的定义是上述定义的对偶形式.
2) BCK-代数一定是BCC-代数,反之不真.
BZ-代数[73-74]是较BCC-代数更广泛的代数系统,它也被国外学者称为弱BCC-代数(weak BCC-algebra[75]).
定义20[73]一个BZ-代数(或称弱BCC-代数)是指代数结构(A;→,1),这里≤是L上的二元关系,→是A上的二元运算,1是A中的一个常元,且满足以下条件(∀x,y,z∈A):
(I) (y→z)→((x→y)→(x→z))=1,
(II)x→x=1,
(III) 1→x=x,
(IV)x→y=y→x=1⟹x=y.
在BZ-代数(A;→,1)中定义二元关系≤如下:(∀x,y∈A)x≤y⟺x→y=1,则≤是A上的偏序.可以证明,1是BZ-代数(A;→,1)中的极大元,即(∀x∈A)1≤x⟹x=1.
命题5[76]一个BZ-代数(A;→,1)是BCI-代数当且仅当它满足下列条件之一:
(V) (x→y)→((y→z)→(x→z))=1,∀x,y,z∈A;
(VI)x→(y→z)=y→(x→z),∀x,y,z∈A;
(VII)x→(y→z)=1⟹y→(x→z)=1,∀x,y,z∈A.
一个BCC-代数(A;→,1)是BCK-代数当且仅当它满足(VI)或
(IX)y→((y→x)→x)=1,∀x,y∈A.
定义21[73]一个BZ-代数(A;→,1)称为是群逆的(anti-grouped),如果它满足以下条件
(AG) (x→1)→1=x,∀x∈A.
命题6[73]一个BZ-代数(A;→,1)是群逆的,当且仅当它满足:
(AG1) (x→y)→(x→z)=y→z,∀x,y,z∈A.
定理7[73]设(A;→,1)是一个群逆BZ-代数.定义加法运算+及逆元如下:∀x,y∈A,

则(A;+,1)是群(未必可换).类似地,定义加法运算及逆元如下(∀x,y∈A):
x
则(A;,1)是群(未必可换).



3)x→x=1;
4)x→y=y→x=1⟹x=y;
5)x→y1⟺xy1.





1) 1≤x⟹x=1;

3)x≤y,y≤z⟹x≤z;




8) 1→xx,1xx;





(a) (X;→,1)是一个BZ-代数;




至此,前述的BCK/BCI-代数、BCC/BZ-代数、伪BCK/BCI-代数之间的关系,可用图1直观描述.
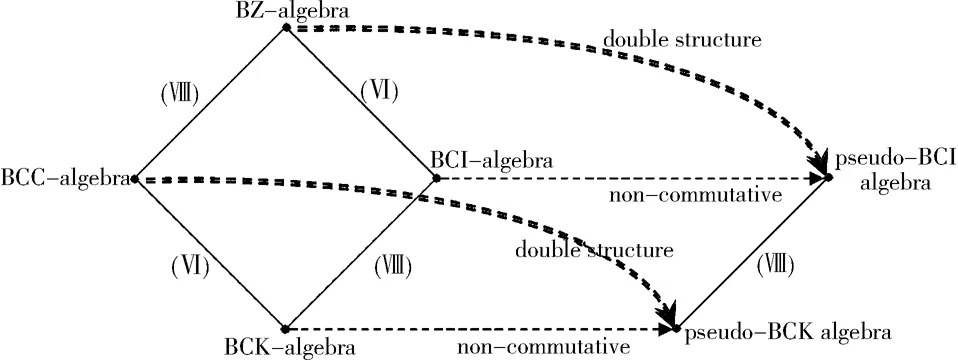
图 1 BCK-、BCI-、BCC-、BZ-代数与伪BCK/BCI-代数之间的关系

不过,前面的例1表明,与非结合t-模相对应的“剩余”不满足BCK/BCC-代数的基本条件.自然产生一个问题:什么样的一般蕴涵代数可以作为各种非经典逻辑代数的公共代数基础?
3.2量子B-代数、基本蕴涵代数与EO-代数1984年Mulvey提出quantale概念,用以研究非可换空间和量子力学.基于quantales导出的蕴涵算子,Rump等在文献[77]中引入量子B-代数(quantum B-algebra)的概念,它包含许多蕴涵代数(比如BCK-代数、MV-代数、BL-代数及其非可换推广)作为特例.关于量子B-代数的一些最新研究,可参见文献[78-82].
定义23一个quantale是一个具有结合二元运算*的完备格Q,满足如下分配性:
1)x*(∨i∈Iyi)=∨i∈I(x*yi),∀x,yi∈Q,i∈I(I为任意指标集);
2) (∨i∈Iyi)*x=∨i∈I(yi*x),∀x,yi∈Q,i∈I(I为任意指标集).

1)y→z≤(x→y)→(x→z);

3)y≤z⟹x→y≤x→z;




2)y≤z⟹x→y≤x→z;




3)y≤z⟹z→x≤y→x;







定理9[77-78]每一个伪BCI-代数是一个单位量子B-代数;一个量子B-代数是伪BCI-代数当且仅当它的单位元是极大元;一个量子B-代数是伪BCK-代数当且仅当它有最大元且该最大元是单位元.
从定义24的1)及2)可以看到,尽管量子B-代数具有一般性,但仍然不能将例1中的蕴涵算子包括进去.因此,有必要对BCK/BCC-代数、量子B-代数等做进一步拓展,以便能概括更一般的蕴涵算子.
实际上,在模糊逻辑及其应用研究中,蕴涵算子一直是人们关注的焦点之一,大量研究文献涉及这一主题(参见文献[83-88]).目前,关于单位区间上的蕴涵算子,常用以下定义.
定义25[83-84]函数I:[0,1]2→[0,1]称为是一个蕴涵(implication),如果它关于第一个变元不增、关于第二个变元不减,且
I(0,0)=I(0,1)=I(1,1)=1,I(1,0)=0.
经过对各种源于非经典逻辑的代数系统进行比较分析,我们与Borzooei及Jun在文献[89]中共同提出一个新的概念:基本蕴涵代数(Basic Implication Algebra,简写为BI-代数),这类代数系统具有较强的概括性,可以包括例1中的蕴涵算子、且能建立起通常的滤子理论和商代数结构.
定义26[89]一个基本蕴涵代数(简称BI-代数)是一个具有二元运算→的偏序集(X,≤),∀x,y,z∈X,满足以下条件:
1)x≤y⟹z→x≤z→y;
2)x≤y⟹y→z≤x→z.
一个基本蕴涵代数X称为正规的(normal),如果X满足:
3) ∀x,y∈X,x→x=y→y;
4) ∀x,y∈X,x≤y⟺x→y=e,这里e=x→x=y→y.
命题10[89]设(X;≤,→)是一个基本蕴涵代数(BI-代数),则(∀x,y,u,v∈X):
1)x≤y⟹y→x≤x→x≤x→y;
2)x≤y⟹y→x≤y→y≤x→y;
3)x≤y且u≤v⟹y→u≤x→v;
4)x≤y且u≤v⟹v→x≤u→y.

有趣的是,一些学者在文献[90-91]中引入扩展序代数(Extended-Order Algebra,简写为EO-代数)的概念,它正好是一种特殊的基本蕴涵代数(BI-代数).
定义27[90-91]一个弱扩展序代数(weak extended-order algebra,简写为w-eo algebra)是一个三元组(X,→,┬),其中X是非空集,→是X上的二元运算,┬是X上的常元,∀a,b,c∈X,且满足以下条件:
(O1)a→┬=┬;
(O2)a→a=┬;
(O3) 如果a→b=┬且b→a=┬,则a=b;
(O4) 如果a→b=┬且b→c=┬,则a→c=┬.
在弱扩展序代数(X,→,┬)上定义如下关系≤:(∀a,b∈X)a≤b⟺a→b=┬,则(X,≤)是偏序集,┬为顶元.
定义28[90-91]一个三元组(X,→,┬)称为是右弱扩展序代数(right w-eo algebra),如果它满足前述公理(O1)、(O2)、(O3)和以下的公理(O5):
(O5) 如果a→b=┬,则(c→a)→(c→b)=┬.
一个三元组(X,→,┬)称为是左弱扩展序代数(left w-eo algebra),如果它满足前述公理(O1),(O2),(O3)和以下的(O5’):
(O5’) 如果a→b=┬,则(b→c)→(a→c)=┬.
一个三元组(X,→,┬)称为是扩展序代数(extended-order algebra,简写为EO-algebra),如果它既是右弱扩展序代数、又是左弱扩展序代数.
容易验证,右弱扩展序代数、左弱扩展序代数均满足公理(O4).
命题12设(X,→,┬)是一个扩展序代数(EO-代数),则(X;≤,→,┬)是一个以┬为最大元的正规基本蕴涵代数.
4 结论及进一步研究的课题
从以上对非经典逻辑代数的系统比较分析可以看出,BCK-代数是各种t-模基模糊逻辑及相关非经典逻辑系统(蕴涵片段)的代数抽象,BCC-代数是各种伪t-模基模糊逻辑及相关非经典逻辑系统(蕴涵片段)的代数抽象,而基本蕴涵代数(BI-代数)是各种广义t-模(包括非结合t-模、半一致模等)基模糊逻辑及相关非经典逻辑系统(蕴涵片段)的代数抽象.同时,我们在文献[89]的研究结果表明,各种非经典逻辑代数的滤子及商代数理论,可以在基本蕴涵代数(BI-代数)的一般框架下统一处理.
作为进一步研究的课题,以下问题具有重要意义:
1) 与非结合t-模、半一致模相关的剩余格序广群的滤子理论及特殊子类(比如非结合BL-代数、非结合Hoop代数、非结合非交换BL/Hoop-代数等)的特性等;
2) 蕴涵运算与传统代数运算之间的深层次联系,比如文献[71,76,92-93]中涉及的群(或半群)与相关蕴涵代数之间的关系研究,需要进一步拓展到更广泛的情况(比如广群与基本蕴涵代数);
3) 非可换且非结合的模糊逻辑形式系统的进一步研究,以及相对应的一般(指非可换或非结合)区间值模糊逻辑、直觉模糊逻辑、二型模糊逻辑、基于粗糙集的逻辑等均具有重要研究价值.
