区间值模糊图的图塔分解与表示定理
2019-01-18李红霞巩增泰
李红霞, 巩增泰, 刘 坤
(1. 陇东学院 数学与统计学院, 甘肃 庆阳 745000; 2. 西北师范大学 数学与统计学院, 甘肃 兰州 730070)
模糊图(可视为欧拉图的推广)是1975年由Rosenfeld[1]定义的,并且给出了与图对应的模糊概念(如模糊桥、路、圈、树以及连通性)及其性质;之后文献[2-3]给出模糊图的笛卡尔乘积、合成及并与联运算;Bhattacharya[4]给出模糊割点、桥及连通性等概念;有关模糊图的运算及相关性质可参阅文献[5-7];Ju等[8]给出区间值模糊图的概念;接着Akram等[9]定义区间值模糊图的笛卡尔积、合成、并、联与补运算,并且讨论了它们的一些性质;Talebi等[10]讨论了自补和自弱补区间值模糊图及其运算;文献[11]给出完全区间值模糊图的一些相关运算.同时,杨文华等[12-13]就区间值模糊图的运算性质给出补充研究;赵衍才等[14]给出模糊图的(α,β)-截图,借助于截图来研究模糊图.对于图G=(V,E)上的区间值模糊图,一方面有类似于区间值模糊集的性质,另一方面,由于[0,1]上区间集和图集的偏序关系,使得区间值模糊图的结构更为复杂.本文利用偏序集的同构关系研究区间值模糊图的图塔分解与表示.对于给定的区间值模糊图,唯一确定[0,1]上区间集的1个划分,同时得到模糊图的图集表示,并证明区间划分与图集有相同的序结构,同时给出区间值模糊图的图塔分解及运算法则,建立区间值模糊图塔与区间值模糊图的同构关系.作为模糊图运算及其应用的基础性研究,得到图集与区间值模糊图的转换定理.
1 基本知识
设I={[a,b]|0≤a≤b≤1}(即[0,1]中所有闭区间构成的集合),I中的序关系定义为:[a1,b1]≤[a2,b2]⟺a1≤a2且b1≤b2,∀[a1,b1],[a2,b2]∈I.

设λ∈I-{[1,1]},若对I的任意有限子集J,当λ≥∧J时,有μ∈J,使得λ≥μ,则称λ为素元,I中素元的全体记作Pr(I)[15].
设λ∈I-{[0,0]},若对I的任意有限子集J,当λ≤∨J时,有μ∈J,使得λ≤μ,则称λ为余素元,I中余素元的全体记作CPr(I)[15].
定义1.1[11]1) 设X是一个非空集合,称映射A:X→I为X上的区间值模糊集,记A(x)=[A-(x),A+(x)](x∈X),显然,A-、A+均为X到[0,1]的映射,且满足
A-(x)≤A+(x)(x∈X).
2) 对于任意的集合V,在V×V-{(x,x)|x∈V}上定义等价关系~如下:
(x1,y1)~(x2,y2)⟺(x1,y1)=(x2,y2)或者x1=y2,x2=y1,
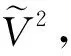
定义1.2[16]设G1=(V1,E1),G2=(V2,E2)是图.
1) 称图G=(V1∪V2,E1∪E2)为图G1与G2的并,可记为G=G1∪G2;
2) 称图G=(V1∩V2,E1∩E2)为图G1与G2的交,可记为G=G1∩G2;
3) 若V1⊆V2,E1⊆E2,则称G1是G2的子图.


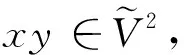

则称序对G=(A,B)是图G=(V,E)的区间值模糊图.记图G上的区间值模糊图的集合为IF(G).
对于G1=(A1,B1),G2=(A2,B2)∈IF(G),定义运算如下:
G1∨G2=(A1∨A2,B1∨B2),
其中∀x∈V,yz∈E,(A1∨A2)(x)=A1(x)∨A2(x),(B1∨B2)(yz)=B1(yz)∨B2(yz).
G1∧G2=(A1∧A2,B1∧B2),
其中,∀x∈V,yz∈E,(A1∧A2)(x)=A1(x)∧A2(x),(B1∧B2)(yz)=B1(yz)∧B2(yz).
定理1.4[12]设G=(V,E)是1个图,G=(A,B)是G上的区间值模糊图当且仅当对于任意的λ∈I,Gλ=(Aλ,Bλ)是图,其中
Aλ={x∈V|A(x)≥λ},
Bλ={xy∈E|B(xy)≥λ}.
2 区间值模糊图的划分区间及图表示
类似于模糊集的分解定理与表示定理,区间值模糊图可用其水平截集—子图集来表示.由于[0,1]上的区间集是偏序集,可以将其分解为素元或余素元,从而得到相应于区间值模糊图的[0,1]上区间集的划分,区间值模糊图用图集表示,且图集与[0,1]上区间集的划分有相同的链式结构.反之,划分有相同序结构的图集和[0,1]上区间集,可以确定一个区间值模糊图.
定理2.1设G=(A,B)是G=(V,E)上的区间素元值模糊图(即∀x∈V,yz∈E,A(x),B(yz)∈Pr(I)),则有
Gλ∧μ=Gλ∪Gμ, ∀λ,μ∈I,
证明只需证明Aλ∧μ=Aλ∪Aμ,Bλ∧μ=Bλ∪Bμ对λ,μ∈I成立.∀λ,μ∈I,若Aλ∧μ=Φ,结论是显然的.否则∀x∈V且x∈Aλ∧μ,有A(x)≥λ∧μ,由A(x)∈Pr(I),则A(x)≥λ或者A(x)≥μ,于是x∈Aλ或者x∈Aμ,即x∈Aλ∪Aμ.另一方面,若x∈Aλ∪Aμ,有A(x)≥λ或者A(x)≥μ,则A(x)≥λ∧μ,也就有x∈Aλ∧μ.
类似地,可以得到Bλ∧μ=Bλ∪Bμ.
定理2.2设G=(A,B)是G=(V,E)上的区间值模糊图,则对λ,μ∈I,有
Gλ∨μ=Gλ∩Gμ.
证明只需证明Aλ∨μ=Aλ∩Aμ,Bλ∨μ=Bλ∩Bμ对λ,μ∈I成立.∀x∈V且x∈Aλ∨μ,有A(x)≥λ∨μ,则A(x)≥λ且A(x)≥μ,即x∈Aλ且x∈Aμ,于是x∈Aλ∩Aμ.另一方面,对x∈Aλ∩Aμ,有A(x)≥λ且A(x)≥μ,即A(x)≥λ∨μ,于是
x∈Aλ∨μ.
类似地,可得到Bλ∨μ=Bλ∩Bμ.

∀λ∈CPr(I),


类似地,可得
例2.4设G=(A,B)是G=(V,E)上的区间值模糊图,其中
V={vi},i=1,2,3,4,
E={v1v2,v2v3,v1v4,v1v3,v3v4},
将G分解为区间值模糊图G1=(A1,B1)与G2=(A2,B2)的并,其中
于是
G[a,a]=(G1)[a,a]∪(G2)[a,a]=
G[0,b]=(G1)[0,b]∪(G2)[0,b]=
于是
Gλ=G[a,a]∩G[0,b]=
进一步,根据GI对I进行划分,所得的划分与GI是同构的.
设G=(A,B)是G=(V,E)上的区间值模糊图.记H(G)={λ∈I|A(x)=λ或B(yz)=λ,x∈V,yz∈E}.I上的一个二维关系“≈”定义为:对于λ,μ∈I,λ≈μ当且仅当Gλ=Gμ,显然“≈”是I上的一个等价关系.记λ≈={μ∈I|λ≈μ},则I/≈是I的商集.
性质2.5设G=(A,B)是G=(V,E)上的区间值模糊图,λ,μ∈I,则λ≈μ当且仅当↑λ∩H(G)=↑μ∩H(G)(↑λ={h∈I|h≥λ}).
证明对λ,μ∈I,λ≈μ当且仅当Gλ=Gμ,即Aλ=Aμ,Bλ=Bμ,当且仅当对x∈V,yz∈E,有
A(x)≥λ⟺A(x)≥μ,B(yz)≥λ⟺B(yz)≥μ,
当且仅当{x∈V|A(x)∈↑λ}={x∈V|A(x)∈↑μ},{yz∈E|B(yz)∈↑λ}={yz∈E|B(yz)∈↑μ},当且仅当
↑λ∩H(G)=↑μ∩H(G).
由I中的≤可诱导I/≈的一种序关系:对λ,μ∈I,λ≈≤μ≈当且仅当↑μ∩H(G)⊆↑λ∩H(G).
性质2.6设G=(A,B)是G=(V,E)上的区间值模糊图,则λ≈≤μ≈当且仅当Gμ⊆Gλ.
证明对λ,μ∈I,λ≈≤μ≈当且仅当↑μ∩H(G)⊆↑λ∩H(G),当且仅当
{x∈V|A(x)∈↑μ}⊆{x∈V|A(x)∈↑λ},
{yz∈E|B(yz)∈↑μ}⊆{yz∈E|B(yz)∈↑λ},
当且仅当Aμ⊆Aλ,Bμ⊆Bλ,也就是Gμ⊆Gλ.
性质2.7设G=(A,B)是G=(V,E)上的区间值模糊图,则对x∈V,yz∈E,A(x)=∨[A(x)]≈,B(yz)=∨[B(yz)]≈.
证明∀x∈V,λ∈[A(x)]≈,则A(x)≥λ.又A(x)∈[A(x)]≈得A(x)为[A(x)]≈的上确界.类似地,对yz∈E,B(yz)=∨[B(yz)]≈.



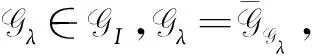


由此,对于例2.4中的区间值模糊集,可以得到它的规范表示:

反之,根据以上图G=(V,E)的子图集和区间级I的划分,很容易得到图G=(V,E)上的区间值模糊图.
性质2.10设{Gi=(Vi,Ei)}(i=1,2,…,m)为图的子图集,{[ai,bi]≈}(i=1,2,…,m)为I的商集,且满足Gi⊆Gj当且仅当[ai,bi]≈≥[aj,bj]≈,那么G=(A,B)是G=(V,E)上的区间值模糊图,其中,A(x)=∨{[ai,bi]≈|x∈Vi},B(yz)=∨{[ai,bi]≈|yz∈Ei}.
3 区间值模糊图与图塔
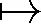
定义3.2对任意的f,g∈T(G),规定T(G)的运算如下:
(f∪g)(λ)=f(λ)∪g(λ),λ∈I,
(f∩g)(λ)=f(λ)∩g(λ),λ∈I.

定理3.4设f∈T(G),则∀λ1,λ2∈I,λ1≤λ2,有f(λ1)⊇f(λ2).

所以f(λ1)⊇f(λ2).
定理3.5设f∈T(G),G=(V,E).令
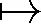
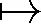
1) 对λ1,λ2∈I,λ1<λ2,有lf(λ2)⊆uf(λ1);
2) 对任意的λ∈I,uf(λ)⊆f(λ)⊆lf(λ);



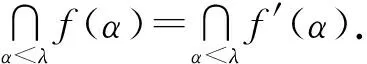
证明只需证lf(λ)=lf′(λ)等价于uf(λ)=uf′(λ).

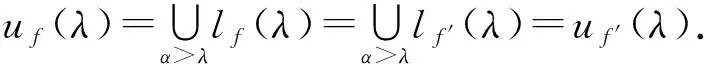





1) 首先证明σ是双射.
uf(λ)=uf′(λ)⊆f′(λ)⊆lf′(λ)=lf(λ),
且uf(λ)⊆f(λ)⊆lf(λ),于是∀x∈V,有




2) 其次证明σ是同态的.

致谢陇东学院博士科研启动资金资助项目(XYBY05)和陇东学院青年科技创新项目(XYZK1708)对本文给予了资助,谨致谢意.
