多单位网上拍卖中的托投标分析

王 宏

(南京审计大学 经济学院/社会与经济研究院，江苏 南京 211815)

一、 引言

网上拍卖中欺诈行为的兴起主要是由于交易者的真实身份很容易伪装，而且往往很难被侦测出来。现实中拍卖的欺诈行为屡见不鲜，如不交送货物、不付款、虚假描述、追加费用和三角诈骗等，对于这些关于信任缺失的一般性欺诈问题，比较容易发现而且也容易治理。但是欺诈中最为广泛而又难以侦测的是卖者的托投标行为。Klemperer认为匿名投标虽然可以有效抵制英式拍卖中的竞标者合谋，但随着匿名投标在网上拍卖中的普及，使得英式拍卖难以抵制卖者以托投标的方式进行自合谋[1]。网上拍卖中匿名交易的本质使得类似于托投标的欺诈变得较为容易。

本文所研究的托投标是指卖者把自己伪装成一个合法的买者进行投标来人为推高拍卖价格的行为，其目的是为了增加拍卖收益而不是想赢得拍卖。托投标除了可以抬高拍卖商品价格，实际上还可以给卖者带来其他收益：(1)Kauffman & Wood认为，卖者可以通过在拍卖开始时设定较低的保留价格，随后通过托投标来对保留价格进行重新设定，这样就可以降低陈列费用(listing fee)*[2]①在实践中，拍卖网站向卖者征收的陈列费与卖者事先设定的保留价格正相关，也就是说，保留价格越高则卖者向拍卖网站支付的陈列费也就越高。；(2)如果还没有竞标者来竞价，卖者可以通过托投标来启动竞价。在拍卖开始时的托投标具有促销的效果，而且参与的竞标者越多，对卖者就越有利[1]。托投标可以获利的逻辑依据为：卖者可以像竞标者经常做的那样[3]，在公开口头报价中通过从以往的竞标过程中学习来更新自己的竞标策略；卖者将托投标作为一种无成本或者低成本的方式来迫使高估价的竞标者报较高的价格；托投标的可能性极大降低了卖者在事前(ex ante)就设定最优保留价格的压力。在独立私有价值的英式拍卖中的托投标等价于卖者在拍卖过程中对保留价格进行了重新设定，他可以以一个比较低的保留价格开始然后通过托投标来对保留价格进行重新设定。由于开始时较低的保留价格有利于吸引更多的竞标者，而这为卖者参与托投标提供了另外的激励。而且，英式拍卖升价竞标的特性给卖者选择最优的托投标策略提供了充分的准备时间。

早期的关于网上托投标的理论研究主要在独立私有价值的英式拍卖框架下，假设参与者数量已知，将托投标行为作为卖者提高自身收益的一种额外手段来进行分析的[4-7]。 在非对称的纯私有价值模型中，Graham首次指出在英式拍卖中托投标能够提高卖者的收益，是因为卖者可以通过托投标将保留价格的设定建立在拍卖的历史信息的基础上[4]。Lopomo在Milgrom & Weber(下文简称为MW)的框架下分析了英式拍卖中卖者以非匿名方式参与托投标的行为，并假定卖者也有可能以正的概率赢得物品[8-9]。由于卖者的行为是透明的，从而就不会影响潜在买者的信念，这样在一系列稳健机制中，存在策略性卖者的英式拍卖就是最优机制。类似地，Lamy在MW关联价值模型的基础上，引入卖者的托投标行为，结果表明托投标效应能够抵消连接原理(linkage principle)所产生的收益，这样就使得卖者在第一价格拍卖中获得的期望收益要高于第二价格拍卖[10]，这就与MW在不考虑托投标的关联价值模型中得到的两种拍卖收益的排序相反。Milgrom & Weber首次提出关联价值拍卖模型，并表明由于连接原理的存在，卖者在第二价格拍卖中获得的期望收益要高于第一价格拍卖[9]。Sher在组合采购拍卖的VCG机制中考察了买者如何通过采用最优的托投标来最小化采购成本的问题，研究发现与不存在托投标下的VCG机制只存在非占优策略的唯一均衡相比较，托投标的存在可能会导致非占优策略的多重均衡，而且在不同均衡下会导致不同的支付[11]。他发现为了使得自己的托投标是最优的，参与托投标的买者之间应该尽可能地避免竞争，每个参与托投标的买者应该只在他最有可能赢标的物品组合上进行竞价。但是他们的结论依赖于很强的假设，即参与托投标的买者准确地知道所有其他竞标者的报价。

由于在网上拍卖中很难侦测出托投标行为，相关的拍卖信息和数据往往比较敏感而且是保密的，从而使用经验数据来考察托投标对于竞标行为和结果的影响就存在较大的现实困难，因此现有的关于托投标的实证研究大多采用了实验方法。Kauffman & Wood的实证结果表明托投标的存在极大地降低了起拍价并延长了拍卖的持续时间[2]。Katkar & Reiley在eBay上通过田野实验(field experiment)检验了使用隐藏保留价格的收益[12]。他们的结论表明，与隐藏保留价格相比较，公开保留价格能使卖者获得更多的收益。Engelberg & Williams 从实证分析的角度表明了，eBay的代理竞价系统(proxy bidding)给卖者参与托投标提供了空间，卖者通过增量竞价的方式将物品价格推高到当前的最高报价且保证自身不会成为最高报价者，同时由于eBay本身能够从托投标中获得收益从而就没有激励采取措施来减少托投标行为[13]。Kosmopoulou & De Silva在共同价值拍卖框架下，通过一系列实验探讨了托投标对于拍卖价格和收益的影响[14]。他们发现如果买者意识到卖者参与托投标的可能性，卖者利润反而会减少，通过降低拍卖价格托投标减轻了赢者诅咒(winner’s curse)，这样托投标反而有利于买者。

现有相关研究的缺陷主要有：(1)大多是在单物品网上拍卖的背景下考察托投标行为，而实际上托投标更容易出现在多物品拍卖中；(2)大都假设参与拍卖的竞标者数量是固定的，而实际上在网上拍卖中竞标者数量不是固定的，竞标者是随机到达拍卖的，其到达速率对于卖者的最优托投标有重要影响；(3)没有认识到卖者能够利用自身的信息优势来参与托投标，即卖者实际上可以基于之前的竞标信息来决定自己的最优托投标，这就使得现有的一些防范托投标的建议和措施存在局限性。

本文在多单位的网上英式拍卖中，考虑竞标者随机到达，求解了诚实竞标者对抗托投标的均衡竞标策略，尽管该竞标策略在阻止托投标上的作用有限。此外，更为有效地抵制托投标的措施可能包括吸引更多的潜在竞标者以及限制在单次拍卖中销售的物品数量。更进一步，我们考虑竞标者的随机到达，并假设卖者能够利用过去的竞标信息来对当前竞标者估价的分布进行贝叶斯更新，从而就能利用这种更新后的预测来决定最优的托投标。不管存在唯一的还是多重的最优托投标，卖者总能根据这种贝叶斯更新将自己的托投标动态调整到最优水平。更为重要的是，诚实竞标者对于托投标的策略性响应促使卖者更为积极地调整他的托投标。

二、 模型设定

一方面，一个诚实的竞标者i顶多只能竞标到他自己的私人估价，即vi≥bi(vi)，另一方面一个不诚实的卖者可以伪装成竞标者j提交托投标，他可以报托投标到他自己的私人估价v0之上以推高竞价，即bj(vj)≥v0。为了分析的方便我们假设提交托投标的卖者赢得拍卖的概率为零。因此，他的托投标应该低于赢标者i的估价，即bj(vj)≤vi。

假设卖者设定的保留价格为r。传统的拍卖模型都假设卖者在拍卖前向拍卖平台承诺设定一个保留价格，该保留价格在拍卖过程中不允许被更改。然而，卖者在竞标过程中可以推断竞标者的估价分布，通过提交托投标来有效地更改他在拍卖开始时设定的保留价格。在这里假设卖者与其他的诚实竞标者是不对称的，因为卖者知道谁是诚实的竞标者，这种假设与类似于Amazon的软结束拍卖(soft-close auctions)是相符合的，而与类似于eBay的硬结束拍卖(hard-close auctions)是不符合的，因为在硬结束拍卖中一些竞标者仅在最后的时刻提交报价，这样卖者就没有充足的时间进行托投标。

三、 存在卖者托投标下的均衡竞标策略

接下来我们在多单位歧视性价格拍卖的背景下，考察存在卖者托投标的情况时，诚实竞标者应该采取怎样的均衡竞标策略。在固定其他竞标者策略的条件下，该竞标策略能使得某个竞标者的期望效用实现最大。由于在歧视性价格拍卖中竞标者一旦赢标将会支付自己的报价，因此赢标者的期望收益就是他的私人估价与期望支付之差，从而某个竞标者的期望收益可以表示为：

竞标者期望收益=赢标概率×(竞标者的私人估价-报价)=赢标概率×(vi-bi(vi))

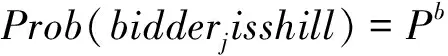
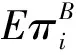
(1)

一般而言，卖者的托投标都会比他自身的私人估价要大。由于竞标者被假设为是风险中性的，他的目标就是为了实现期望效用的最大。所有的诚实竞标者根据对称竞标策略进行投标，为了找到均衡竞标策略，我们可以求等式(1)的导数并令其为零，均衡竞标策略bi(vi)由下面定理1所给出。

定理1：在IPV模型下，假设拍卖的参与者都是风险中性的，卖者在拍卖开始时设定的保留价格为r，卖者通过歧视性价格的网上英式拍卖来销售k个单位的同质物品而且卖者进行托投标的概率为Pb时，则在贝叶斯纳什均衡中，每一个诚实竞标者的均衡竞标策略由下面等式的不动点给出：

(2)

(3)

为了得到均衡竞标策略，我们对等式(3)求关于bi(vi)的最优化的一阶条件：

-[Pb·F(φi(bi(vi)))+(1-Pb)·F(bi(vi))]n-k+(vi-bi(vi))·(n-k)·

[Pb·F(φi(bi(vi)))+(1-Pb)·F(bi(vi))]n-k-1·[Pb·f(φi(bi(vi)))·

φi′(bi(vi))+(1-Pb)·f(bi(vi))]=0

(4)

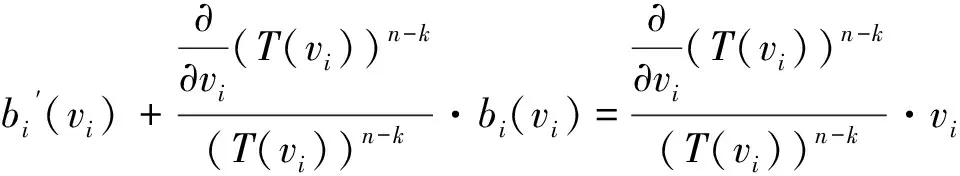
(5)

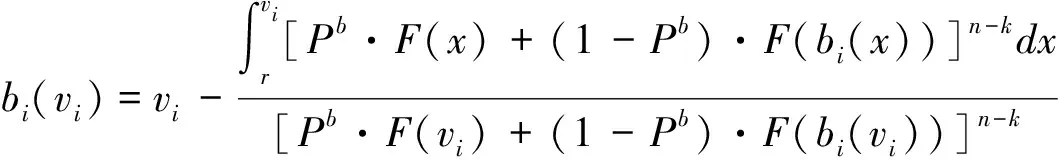
我们可以验证上面的均衡竞标策略是vi的单调增函数，即∂bi(vi)/∂vi>0，这保证了具有最高估价的k个竞标者赢得拍卖。当诚实的竞标者知道卖者会参与托投标时，他们会在竞标策略上产生策略性响应。为了减轻托投标给自己带来的负面影响，他们在多单位的网上英式拍卖中将隐藏报价，进一步可知，他们隐藏报价的程度与卖者参与托投标的概率正相关。

同时，由于在等式(2)中，x≤vi⟹F(x)≤F(vi)，bi(x)≤bi(vi)⟹F(bi(x))≤F(bi(vi))，很容易得到:

这样，根据定理1所给出的均衡竞标策略，我们可以看到随着拍卖物品数量的增加，诚实竞标者隐藏报价的程度也越大。从竞标者的角度来看，这可能意味着当有更多物品在网上拍卖时，卖者参与托投标的机会也越多，这样他们为了避免更多的收益损失从而更多的隐藏其报价。

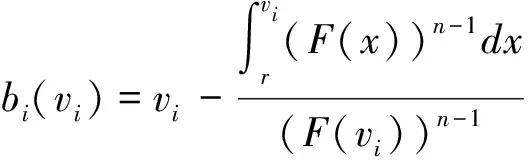
推论1所给出的均衡竞标策略正是由Riley 和Samuelson所求解的最优第一价格拍卖中的均衡竞标策略[15]。在单物品的英式拍卖中，诚实的竞标者如果使用这样的均衡竞标策略，他们将不再报自己的真实估价而是会隐藏报价，而卖者只会获得第二高的报价，这样与竞标者不采取这样的对抗性竞标策略相比较，卖者将会面临着期望收益上的损失。因此，我们可以认为，当诚实的竞标者遵从这样的策略，他就可以对卖者的托投标产生一定的对抗作用。

四、 托投标的获利性分析

卖者参与托投标为什么是有利可图的呢？这是我们接下来所要讨论的问题。为了比较卖者参与和不参与托投标时期望收益的变化，我们首先要计算当卖者没有参与托投标，竞标者也没有必要在竞标策略上做出响应时卖者的期望收益，同时，当卖者参与托投标时我们假设诚实竞标者会意识到托投标的可能存在并采取对抗性竞标策略。独立私有价值的假设是拍卖分析的基准模型，从机制设计的角度来看，在独立私有价值的拍卖环境下，多单位的Vickrey拍卖与最优机制会给卖者带来相等的期望收益。因此，诚实的竞标者在给定不存在卖者的托投标下，卖者在多单位网上英式拍卖中获得的期望收益与多单位Vickrey网上拍卖中获得的期望收益相等。

我们现在采用上面的分析结论，假设卖者现在使用多单位Vickrey网上拍卖机制来销售物品。在多单位Vickrey网上拍卖中，所有赢标者支付相同的价格，该价格等于最高被拒绝的报价。设bi(vi)表示竞标者i的竞标策略，使用Vickrey拍卖中获得的直觉我们知道bi(vi)=vi是竞标者i的占优策略。

假设v(1),v(2),…v(n)表示竞标者估价的顺序统计量，其中v(1)是最高的报价，v(2)是次高报价，并依次类推。我们知道依次具有私人估价v(1),v(2),…v(k)的竞标者赢得拍卖，在不存在托投标时他们都支付同一的拍卖价格v(k+1)。为了方便起见，我们假设竞标者的私人估价服从均匀分布。为了计算E[v(k)|n]，我们先给出[v(k)|n]：

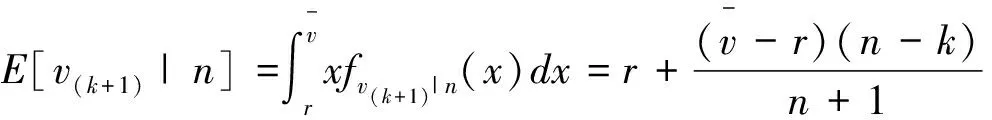
(6)

上面的等式给出了在多单位Vickrey网上拍卖中，当卖者不参与托投标时从拍卖中获得的每单位物品的期望支付价格。从上面的分析中我们知道，(6)式同样是不存在托投标情况下卖者通过多单位歧视性价格的网上英式拍卖所获得的每单位物品的期望支付价格。设πshill和πnoshill分别表示卖者参与和不参与托投标时的期望收益，于是卖者不参与托投标时的均衡期望收益可以表示为：

(7)

为了在均匀分布的假设下求解卖者参与托投标时的均衡期望收益，我们由定理1得到下面的推论2。

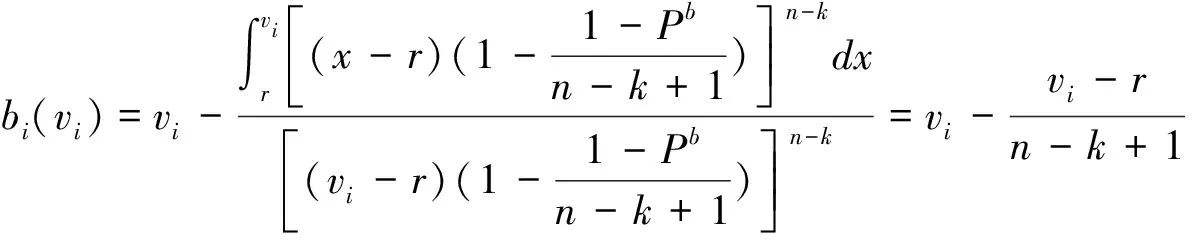
在k单位的网上英式拍卖中如果存在卖者的托投标，k个最高报价的竞标者将赢得拍卖，并支付他们自己的报价。由推论2的结论，卖者参与托投标时的均衡期望收益可以表示为：

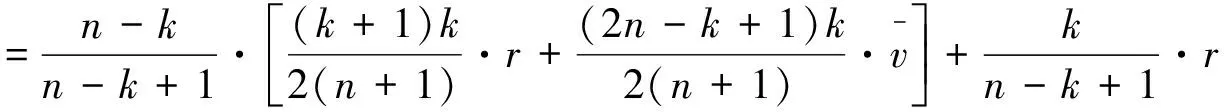
(8)

现有的相关研究只是给出了卖者通过托投标获利的实证证据，但是没有进行相应的理论分析，更没有考虑竞标者在竞标策略上对于托投标的策略响应。Kauffmann & Wood提供了卖者通过重新设定保留价格参与托投标从而来避免eBay收取高额陈列费的证据[2]，Engelberg & Williams提供了卖者通过增量竞价参与托投标进行获利的证据[13]。

从表1可以看出，给定k，ξ随着n的增加而减少；同时，给定n，ξ随着k的增加而增加。参与拍卖的竞标者越多，在单次拍卖中销售的物品数量越少，则卖者参与托投标和不参与托投标下的期望收益之差就会越小。这样的结论提醒我们，为了有效地抵制网络拍卖中的托投标，我们应该采取措施吸引更多的潜在消费者参与竞标，同时要严格限制在单次拍卖中销售的物品数量。

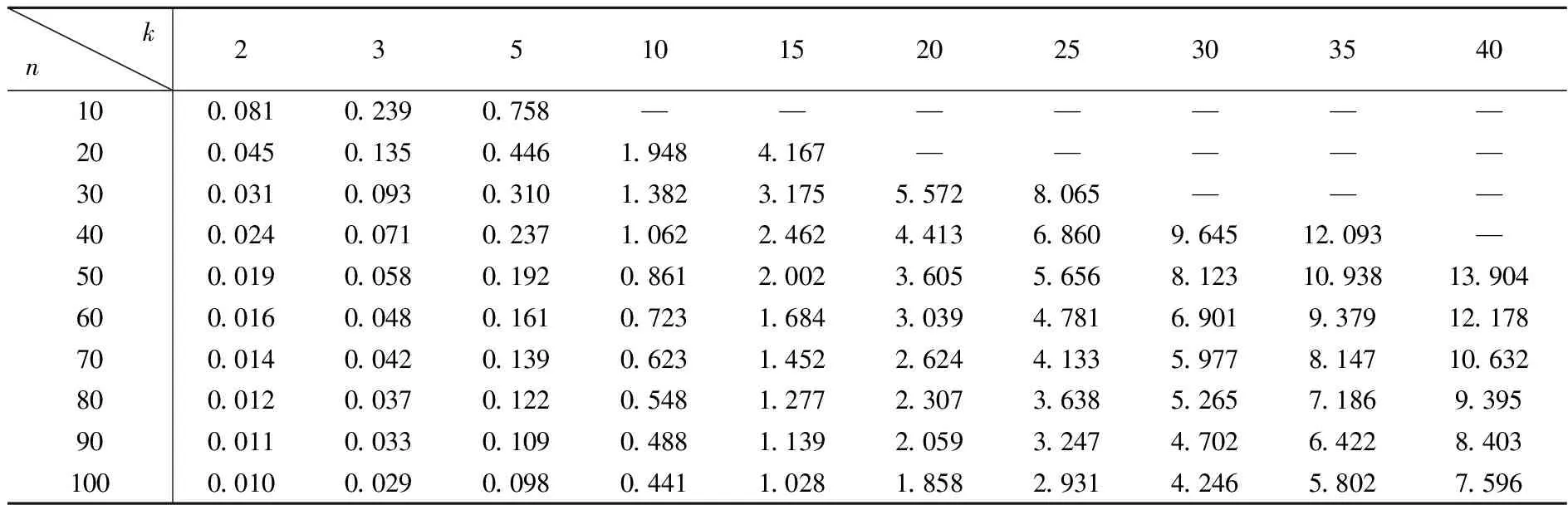
表1 在不同的n和k下ξ的数值变化

五、 基于竞标者随机到达的最优托投标

(一) 竞标者随机到达的相关假设

(二) 求解卖者的最优托投标

当诚实的竞标者采取由前面的定理1所给出的对抗性竞标策略，而且竞标者到达拍卖的过程服从非平稳的泊松分布时，一个重要问题就是卖者最优的托投标是多少。为了回答这个问题，我们首先考虑当只有k个竞标者留下的简单情形。在英式拍卖中，托投标起着在竞标过程中动态的重新设定保留价格的作用。竞标者常常会相信他们参加的是一个事先就设定好了保留价格的拍卖，而实际上保留价格总会根据当前的竞价情况进行动态调整。当有k单位物品待售时，在网上英式拍卖的最后阶段会有k个竞标者留下来，从而卖者可以简单地认为只有k个竞标者留下来，他通过提交托投标来动态地重新设定拍卖的保留价格。

同时，卖者从竞标过程以及当前的最高报价中可以知道其他(n-k)个竞标者的估价分布。卖者知道所有其他(n-k)个竞标者的估价都不高于b，因此，这些竞标者更新后的累积分布函数为：

卖者可以通过提交托投标s≥b来重新设定保留价格，每个赢标者在拍卖结束后将会向卖者支付他们自己的报价。根据收益等值原理，我们知道卖者在歧视性价格的网上英式拍卖中获得的收益与在Vickrey拍卖下获得的收益相等。由于在目前第(k+1)高的报价为托投标s，在Vickrey拍卖中所有的k个赢标者都会向卖者支付s，从而卖者在Vickrey拍卖中所获得的收益为k(s-v0)，进一步，我们可以知道卖者在歧视性价格的网上英式拍卖中所获得的收益也为k(s-v0)。在最后有k个竞标者会留下来，而且贝叶斯更新后的估价分布为Max，这样卖者提交托投标s≥b的期望收益为：

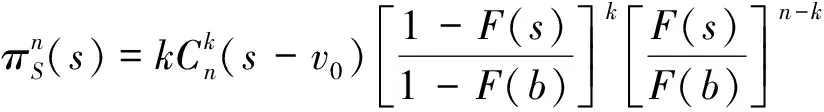
由于n是起初参与拍卖的竞标者数量，且服从泊松分布，对上式取关于n的期望我们得到：

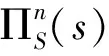
(9)

(s-v0)[1-F(s)]keλF(s)≥(b-v0)[1-F(b)]keλF(b)

(10)

(11)

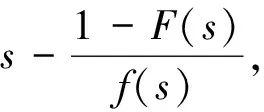
进一步我们从等式(11)中发现，卖者的最优托投标与当前的最高报价b无关，这可能是由于卖者可能经常会更多地关注具有最高估价的k个竞标者的竞标情况，并且将这些竞标信息作为设定最优托投标的基础来尽量避免自己成为赢标者的风险。这个含义与我们模型中关于卖者赢标概率为零的假设是一致的。

定理2：在网上英式拍卖中，当卖者可以连续序贯的增加其托投标时，最优托投标s*由等式(11)所决定，而且最优托投标与诚实竞标者当前的最高报价b无关。

为了进一步加深我们对于等式(11)的理解，我们可以对等式(11)进行以下变形，并将它与传统拍卖理论中的最优保留价格进行比较分析。等式(11)可以变成：

(12)

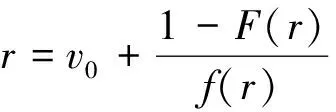
(13)

上面两个等式是类似的，唯一区别是等式(12)中逆风险率需要乘以系数1/[k-(1-F(s))λ]。当卖者需要设定最优的托投标来最大化其期望收益时，这实际上等价于在竞标过程中动态地调整自己的保留价格。尽管竞标者一般都会认为卖者会设定一个稳定的保留价格，而实际上卖者经常会隐藏其保留价格并不断进行动态调整，直到他认为保留价格已经调整到由等式(12)所给出的水平。

(三) 最优托投标的唯一性和多重性

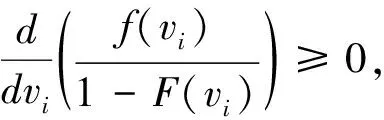
我们接着讨论卖者提交托投标的边际成本的单调性，MC(s)的一阶倒数为：

(1)当k=1时，由MR(s)≥0⟹1-F(s)-(s-v0)f(s)≤0⟹∂MC(s)/∂s≤0，从上面的分析还可以知道∂MR(s)/∂s≥0，因此由等式(10)，即MR(s)=MC(s)所给出的最优托投标是唯一的。

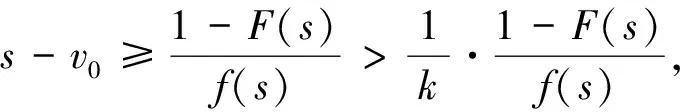
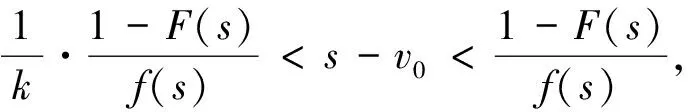
当卖者的最优托投标是唯一时，卖者同样可以在竞标过程中动态调整其托投标。卖者可以先提交一个比较低的托投标，该托投标不一定是最优的，然后根据他所观察到的竞标信息，重新设定托投标直到达到能实现期望收益最大的最优托投标水平。

当F(v)是不同类型竞标者估价分布的组合时，上面的等式(11)有多重解。当存在异质竞标者时，卖者的期望收益可能存在多个局部最优点。许多现实的拍卖中都存在异质的竞标者，比如在艺术和古董拍卖市场，专家和无经验的收藏者就是不同类型的竞标者。在加州高速公路采购拍卖中，存在着事先就已经被承诺获得较大部分工程量的竞标者，他们参与竞标只是为了获得参与权，同时还存在着实力相对弱小的竞标者为了建设合同而参与竞标。在拍卖开始之前，对于竞标者估价分布和参与竞标的竞标者数量的估计可以作为高类型竞标者可能存在的比较好的预测指标。在拍卖过程中，建立在当前的最高报价基础之上，卖者可以对高类型和低类型竞标者的可能存在进行更新估计。我们注意到，即使卖者在事前能准确知道竞标者数量，从而就知道方程(11)的一个全局最大化的解能够使得他的期望收益最大，卖者以一个较低的托投标开始去吸引低类型的竞标者，当目前的最高报价表明可能存在高类型竞标者时他就可以逐渐提高托投标到最大的最优托投标水平。

不管是存在唯一的还是多重的最优托投标，从推论3得到的含义解释了为什么在存在托投标的英式拍卖中，卖者可以获得比在密封拍卖下更高的期望收益，此时经典的收益等值原理不再成立。

六、 结论

网上英式拍卖递增报价的性质使得卖者可以利用过去的竞标信息来设定合意的托投标，并且对自己的托投标策略进行评估，这对我们有效阻止托投标增加了困难。本文求解了诚实竞标者对抗托投标的均衡竞标策略，但是由于卖者总可以观察到诚实竞标者的竞标信息，并据此来决定自己的最优托投标策略，这就减弱了该均衡竞标策略对于托投标的对抗性效果。为了进一步减少卖者参与托投标的激励，我们需要尽可能增加参与拍卖的竞标者数量，同时要限制在单次拍卖中销售的物品数量。

接下来我们指出几个有趣的研究方向，而这也是本文研究的局限性所在。首先，我们的分析建立在独立私有价值基础上，而不是共同价值或者关联价值。托投标在共同价值下可能具有更为严重的负面影响。托投标影响着竞标者如何根据其他竞标者的报价来更新他们自己的估价，因为竞标者不再认为每一个报价都是诚实竞标者所真正愿意支付的价格。同时，在网上英实拍卖中，共同价值拍卖比私有价值拍卖更为普遍。公开的竞标过程允许竞标者观察并交流彼此的估价，在此基础上调整他们自己的估价。这就是为什么大部分拍卖网站，卖者和竞标者偏好英式拍卖的原因之一。直观上，我们可以认为卖者提交托投标的动机就是假装自己是一个竞争性的买者，通过托投标来鼓励一个诚实的高估价买者不仅报高于其真实估价的报价而且在此之外还会相应的提高他的估价。本文中我们只考虑竞标者的估价为私有信息的情形，在以后的研究中，我们应该对网上英式拍卖中的共同价值模型下的托投标进行分析。其次，在多轮独立私有价值的网上英式拍卖中，托投标也有类似的负面影响。在多轮拍卖中考察托投标可能会更加接近现实。尽管我们没有在多轮网上英式拍卖中对于托投标进行理论分析，但是我们相信我们得到的诚实竞标者对抗性的竞标策略在多轮英式拍卖中也能够降低托投标的负面影响，卖者同样可以充分利用过去的竞标信息来选择最优的托投标从而实现期望收益的最大化。诚实竞标者对于托投标的策略性响应给卖者提供了更多的激励去充分利用过去的竞标信息和竞标者的估价分布，更新他对当前竞标者估价分布的预测，而这又能部分抵消竞标者对抗性行为对卖者自己带来的不利影响。最后，由于卖者在信息上的优势，即他可以利用之前的竞标信息来决定自己的最优托投标，这样即使诚实竞标者采取对抗性的竞标策略，卖者依然可以通过参与托投标来获利。从本文研究中得到的一个重要启示就是，通过外在的一些因素来抵制托投标的作用就会非常有限，只有通过结合网上拍卖的特性设计出能够有效抵制托投标的拍卖机制，使得卖者没有激励参与托投标，这样才能实现有效抵制托投标的目标。现有的关于托投标的相关研究只是将传统的离线拍卖机制硬搬到网上拍卖中来，没有考虑网上拍卖的特性，也没有考虑到卖者托投标的动态调整过程，从而就不能有效地侦测出并抵制托投标行为。这正是本文未来的一个重要研究方向。