p-进域上的谱和tiling集的一个刻画

买买提艾力喀迪尔

(喀什大学数学与统计学院,新疆喀什 844006)

1 引言

设G是一个局部紧的Abel群,是其共轭群.假设Ω⊂G具有正有限Haar测度的Borel可测集合,称Ω是一个谱集如果存在G的一个连续特征的集合Λ⊂,使得组成平方Haar-可积可积函数空间L2(Ω)的一个正交基.集合Λ称为Ω的一个谱,(Ω,Λ)称为谱对.我们说一个集合Ω平移地tileG,如果存在一个集合T⊂G使得集族{Ω+t}t∈T构成G的一个划分(除了零测集外).该集合T称为Ω的一个tiling集或者一个平移集,(Ω,T)称为一个tiling对.

当G=Rd时,关于谱集和tile的关系Fuglede[1]提出如下的猜想.

谱集猜想一个具有正有限Lebesgue测度的Borel集Ω⊂Rd是一个谱集当且仅当它是一个平移tile.即存在一个集合Λ使得(Ω,Λ)是一个谱对当且仅当存在一个集合T使得(Ω,T)是一个tiling对.

在任何局部紧的Able群G上可以考虑广义Fuglede猜想:一个正有限Haar测度的Borel集Ω⊂G是谱集当且仅当它是一个平移tile.甚至在有限群上也可以讨论该猜想[2].

我们可以考虑如下的对偶谱集猜想:设Λ⊂G,则Λ是一个谱当且仅当Λ一个tiling集.即存在一个集合Ω使得(Ω,Λ)是一个谱对当且仅当存在一个集合Ω0使得(Ω0,Λ)是一个tiling对.

在欧式空间Rd对于这一谱集猜想的研究取得了一些局部性的结果(见文献[1,3,4]).谱集猜想提出来30年以后,直到2004年菲尔兹奖得主陶哲轩[5]在维数大于等于5的时候构造了一个反例说明谱集未必是tile.现在这些反例的维数降低到d≥3[6,7].至今,谱集猜想在一维或者二维空间上是否成立仍然是一个公开问题.

另一方面,文献[8]研究了Rd上的单位正方形的所有谱的结构,文献[9,10]证明了R上的谱集的谱一定是周期的.

最近,范爱华[11]考虑局部域上的谱集和谱测度问题;本文作者[12]证得当谱或者tiling集是拟格的时候谱集猜想在局部域上的向量空间上成立.谱集猜想在p-进域Qp上完全被解决了.其实,他们[13,14]证得一个有界集Ω⊂Qp是谱集⇔Ω是一个tile⇔Ω是几乎紧开“p-齐次”.同时,他们也证明了Qp上的谱或者tiling集在等距同构的意义下是惟一的.不过,该猜想在上仍然是个公开问题.

2 预备知识

这一部分介绍p-进数域Qp的有关知识,可积函数空间上的Fourier变换,上的谱集准则等相关内容.

2.1 p-进数域Qp

我们首先回顾一下p-进数域.设p≥2是一个素数,Q是有理数域.任何一个非零数x∈Q可以写成,其中v,a,b∈Z,(p,a)=1和(p,b)=1(这里(x,y)表示两个整数x和y的最大公因数).根据Z上的唯一分解定理,这个数v只依赖于x.对于定义vp(x)=v,vp(0)=+∞并且,那么|·|p是一个非阿基米德绝对值.即

(i)|x|p≥0,等于零仅当x=0;

(ii)|xy|p=|x|p|y|p;

(iii)|x+y|p≤max{|x|p,|y|p}.

p-进数域Qp是有理数域Q在p-进绝对值|·|p之下的完备化.事实上,Qp的任何一个元素x都可以写成

这里v(x):=v称为x的p-赋值,并且|x|p=p−v.记进整数环,其实它是以0为圆心的单位圆.

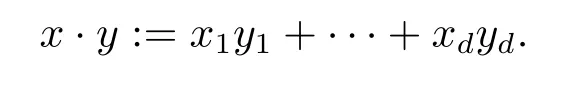
2.2 Fourier变换

注意

Fourier变换具有如下性质

定义2.1定义在上的一个复值函数f称为一致局部常值函数,若存在n∈Z使得

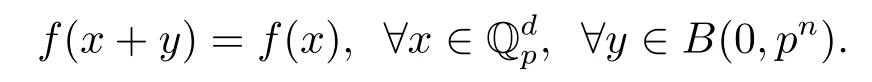
显然一致局部常值函数是连续的.

用|Ω|表示集合Ω的Haar测度.对于一个Borel集使得0<|Ω|<∞,有下面的谱集准则[11].

引理2.2[11]一个Borel集使得0<|Ω|<∞是一个以Λ为谱的谱集当且仅当

下面的引理确定一个正交集E(Λ)中的点应该满足的条件.

引理2.3如果是一个Borel集并且0<|Ω|<∞,那么集合E(Λ)在L2(Ω)内正交当且仅当

若式(2.3)成立,则对任意Λ,有hχλ,χλ0iΩ=0,说明E(Λ)是一个正交集.反过来,若E(Λ)在空间L2(Ω)内的一个正交集,则对任意Λ,有,这个等价于式(2.3).

引理2.4[14]假设是一个Borel集使得0<|Ω|<∞.

(1)若(Ω,Λ)是一个谱对,则Λ是一致离散集合.

(2)若(Ω,T)是一个tiling对,则T是一致离散集合.

取

那么引理2.4表示,如果Λ是集合Ω的一个谱则它是一致离散的并且其分离常数δ(Λ)≥γ0.

3 主要定理及其证明

这一节将介绍主要定理及其证明.

3.1 集合序列的弱收敛

定义3.1设是一个一致离散集合序列,其分裂常数是δ(Λn)≥δ0.集合序列Λn若收敛于一个集合Λ,若对任意η∈N和任意γ∈Z,存在一个自然数N使得对任意n≥N,有

其中Bγ是以原点为球心,以pγ为半径的开球.这个时候极限Λ也是一致离散,并且δ(Λ)≥δ0.

下面的定理是本文的主要结果.

定理3.2设是一个一致离散集合序列,分裂常数是δ(Λn)≥δ0,并且弱收敛于一个集合Λ.假设是一个有界可测集合,并且对任意n,Λn是Ω的一个谱(或tiling集),那么Λ也是Ω的一个谱(或tiling集).

下面介绍这个定理的证明所需要的一系列引理.

3.2 函数tiling

这种情况下,写f+Λ是一个tiling.

如果f=1Ω是一个有界可测集合的示性函数,那么条件(3.1)表示集族{Ω+λ:λ∈Λ}构成的一个划分(除零测集外).这个时候函数tiling就是集合tiling,并且我们说(Ω,Λ)是一个tiling对.

下面的引理给出通过tiling条件来刻画集合Ω的谱的一个方法.

引理3.3假设是一个有界可测集合,定义

证由于引理2.2,我们有(Ω,Λ)是谱对当且仅当对任意,有

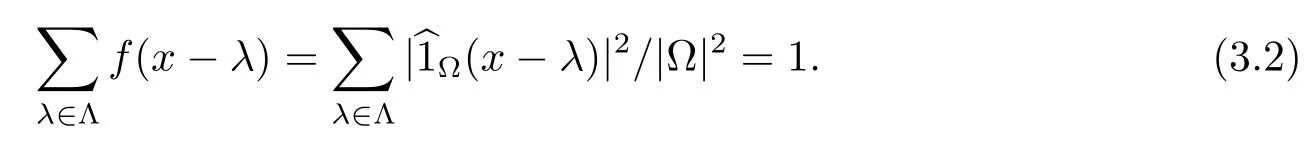
方程(3.2)成立当且仅当f+Λ是一个tiling.

3.3 正交性与填充

这种情况下,写f+Λ是一个填充.注意如果f=1Ω,那么这个表明集族{Ω+λ:λ∈Λ}是两两测度不交.这个时候,我们说(Ω,Λ)是一个填充对.

假设E,F是上的两个离散集合,τ是是的一个向量.设三个集合F,F+τ,F−τ的每一个与集合集合E不交,并且定义

引理3.4令f≥0是上的一个可测函数.假设f+Λ是一个tiling,f+Λ1和f+Λ2是填充,那么f+Λ1和f+Λ2也是tilings.

证定义

(1)fE(x)+fF(x)=1.

(2)fE(x)+fF(x−τ)≤1.

(3)fE(x)+fF(x+τ)≤1.

分别从(2)和(3)减去(1)得到

通过向量τ平移可知,式(3.5)成立等价于fF(x−τ)=fF(x)=fF(x+τ).这个隐含着引理成立.

引理3.5一个指数函数系E(Λ)在空间L2(Ω)内正交当且仅当f+Λ是一个填充,其中.

这个引理的证明完全类似于引理3.3的证明.

运用引理3.3,引理3.4和引理3.5得到

推论3.6假设Λ,Λ1,Λ2是定义在式(3.4),若集合Λ是Ω的一个谱,集族E(Λ1)和E(Λ2)在空间L2(Ω)内正交,则集合Λ1和Λ2也是Ω的谱.

定理3.7设是一个一致离散集合序列,分裂常数是δ(Λn)≥δ0,并且弱收敛于一个集合Λ.假设,并且对任意n,f+Λn是一个tiling,那么f+Λ也是一个tiling.

证假设函数ψ≥0是上的具有紧支撑的局部常值函数并且满足.那么证明对于这种函数ψ如下等式

成立就可以了.

固定一个满足上述条件的函数ψ,定义

由于Λn弱收敛于Λ,所以对任何上的具有紧支撑的局部常值函数ϕ,有

下面给予定理3.2的证明.

定理3.2的证明设是一个有界可测集合.令f(x):=1Ω(x),则,f≥0.根据定理3.7,若对于任意n,Ω+Λn是一个tiling,并且Λn弱收敛于Λ,则Ω+Λ也是一个tiling.