圆锥形单点增量成形件轴向精度研究
2019-01-18张敬冲吴学亮杨明顺袁启龙
张敬冲,李 言,吴学亮,杨明顺,袁启龙
(西安理工大学机械与精密仪器工程学院,陕西西安710048)
金属板料单点增量成形技术是一种新型塑性成形技术,具有成本低、周期短、数字化程度高等特点,已在航空航天、汽车、医疗、艺术品和日常生活等领域有所应用[1]。其成形过程是一个复杂的变形累积过程,涉及工艺参数繁多,存在很多难以预测和控制的成形缺陷,尺寸精度不高已成为制约该技术推广的重要因素。近年来,大量学者对成形机理[2]、成形过程中工艺参数对成形性能的影响[3]、成形工具头的路径优化[4-5]、成形过程的数值模拟[6-7]及非常温成形[8-9]等方面进行了研究。Radu[10]等通过使用响应曲面法和神经网络算法有效地提高了成形件的精度。Guzmn等[11]研究了成形力与成形精度之间的关系,提出了减小成形载荷、提高成形精度的方法。Husain等[12]提出应力比的概念,改变与应力比相关的参数来控制成形件的缺陷。高霖等[13]分析了层间距、成形角、板料厚度和工具头直径等因素对于方锥台件鼓包和材料堆挤等缺陷的影响,通过合理选择工艺参数较好地控制了上述缺陷。韩飞等[14]采用遗传神经网络算法对板料成形过程中的回弹量进行了建模,为金属板料数字化渐进成形回弹量预测开辟了一条新途径。甘文星[15]提出通过使用背压板以及增大成形角度的方法以达到抑制或减小回弹的目的。
综上所述,国内外的科研工作者对成形件精度的研究主要集中在误差产生机理、路径优化、回弹建模等方面,取得了一定的成果。然而,以轴向误差作为研究对象来衡量精度的研究还比较少。为此,本文由成形件轴向误差产生机理作为研究切入点,通过ABAQUS仿真模拟轴向误差在不同工艺参数下的变化规律,然后通过相应实验对其规律进行验证分析,最终实现对轴向误差的预测和控制。
1 轴向误差产生原理
1.1 单点增量成形原理
单点增量成形技术是一种新型的板料柔性塑性成形技术,成形原理类似于3D打印的“分层制造”。首先,根据目标制件的几何形貌,离散生成一系列沿高度方向的等高轮廓层;然后,定制的工具头在机床的控制下沿等高轮廓层逐层挤压板料;最后,被挤压的板料在局部变形的累积作用下,形成了与目标制件形貌一致的成形件,见图1。图1中D是工具头直径,α是成形角,t是板料初始厚度,Z为层间距。本文选择圆锥台作为最终的成形件形状,将圆锥台功能表面轴向高度的实际值与理论值之间求差,即为轴向误差,见图2。

图1 单点增量成形原理图Fig.1 Principle diagram of SPIF

图2 单点增量成形轴向误差示意图Fig.2 Diagram of axial error
1.2 板料回弹造成的轴向误差
单点增量成形过程完成时,由于工具头与板料之间不再有接触,作用在板料上的轴向力会消失,残余应力会使板料沿轴向发生回弹;而将成形件从夹具中取下时,夹具对板料边缘的夹持力突然消失,板料亦会在残余应力作用下发生回弹现象。当回弹量超过一定值时会影响成形件精度,造成几何缺陷,见图3。

图3 成形工件的回弹示意图Fig.3 Springback of forming part
1.3 板料弯曲造成的轴向误差
单点增量成形件的轴向高度是以功能表面的起始处到结束处的垂直距离,其成形过程是以NC程序控制机床进行。程序默认的工件轴向高度起始于板料的上端面,但由于未成形区域会发生不可逆的塑性弯曲变形,故实际的工件功能表面并未起始于板料的上端面平面,在板料弯曲变形处有部分轴向高度损失,如图4所示。

图4 板料弯曲变形示意图Fig.4 Sketch of springback of sheet metal
2 有限元建模
2.1 几何模型
几何模型形状选择典型的圆锥台,圆锥台深度24 mm,顶圆半径45 mm;待成形板料尺寸为140 mm×140 mm的方板;工具头选用球头工具;夹具采用环形夹具,外环半径70 mm,内环半径55 mm。工具头直径、板料厚度、成形角度及底圆半径根据实验条件决定,建立的几何模型见图5,其中板料选用1060铝板,其材料性能见表1,应力应变属性见表2。根据仿真算法特性和成形过程特性,对成形过程采用动力显式算法(Explicit),对成形后夹具卸载过程采用静力隐式算法(Standard)进行模拟。成形过程中的接触方式设为面-面接触,接触算法设为罚函数,摩擦类型设为Coulomb摩擦。对板料进行网格划分,网格属性设为壳单元S4R,边长是1 mm。

图5 仿真模型Fig.5 Simulation model

材料名称密度ρ/(g/mm3)弹性模量E/GPa泊松比γ屈服强度δs/MPa1060铝2.71700.330

表2 1060铝应力应变关系Tab.2 1060 aluminum stress-strain relationship
2.2 动态轨迹加载
为提高仿真效率和精度,以实验所用的NC程序代替传统建模的分析步设置。首先,在Excel中将每行NC代码修改为(X、Y、Z)的坐标格式,并以文档格式另存;然后,通过Matlab对将(X、Y、Z)坐标与时间进行一一对应;最后,将对应关系(X,T)、(Y,T)、(Z,T)导入到ABAQUS中,实现仿真与实验的统一。
在仿真中将单点增量成形的空间轨迹分解成X、Y、Z方向的分运动,利用平滑分析步进行加载,将Matlab提取出的(X,T)、(Y,T)、(Z,T)数据对应到X、Y、Z三个方向运动的幅值中,三个方向的运动在分析步时间内合成即得到成形过程的空间轨迹。
根据上述过程,最终建立的有限元模型见图6,仿真完成后等效应力云图见图7。
3 仿真结果与分析
3.1 模拟仿真方案
单点增量成形过程中工艺参数较多,其对轴向精度影响规律和影响程度各不相同,为研究工具头直径、层间距、进给速度、成形角度、板料厚度等工艺参数对轴向误差的影响,设计正交实验,见表3。

图6 单点增量成形有限元模型Fig.6 Finite element model of SPIF

图7 仿真完成后等效应力云图Fig.7 Stress cloud after simulation

编号工具头直径D/mm层间距Z/mm进给速度v/(mm/min)成形角度α/(°)板料厚度t/mmL160.6100450.6L260.8200530.8L361300601L4100.6100530.8L5100.8200601L6101300450.6L7140.6200451L8140.8300530.6L9141100600.8L1060.6300600.8L1160.8100451L1261200530.6L13100.6200600.6L14100.8300450.8L15101100531L16140.6300531L17140.8100600.6L18141200450.8
当正交实验进行完毕后,会得出各工艺参数对成形精度的影响规律和影响权重,为验证这些结论的正确性,设计单一实验进行验证。然后观察这个实验变量对实验结果的影响。对照正交实验,设计单一实验,见表4。

表4 单一实验参数Tab.4 Single experimental parameters
图8为成形件的半剖图,图中的结点1~2相处同一高度,两节点的距离为制件在此高度处的直径,这条直径线与圆锥台底圆的距离是实际轴向高度,此高度与理论高度值的偏差即是成形件的轴向误差。
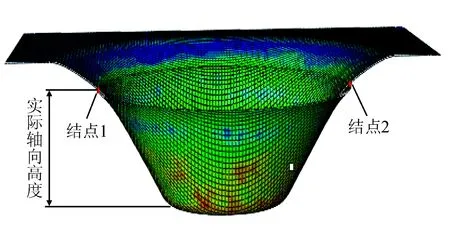
图8 轴向精度测量方法Fig.8 Radial accuracy measurement method
3.2 仿真结果
对模拟结果进行处理,分别求取表3中不同编号实验时成形件轴向误差值ΔH(单位:mm),得出的数据见表5。
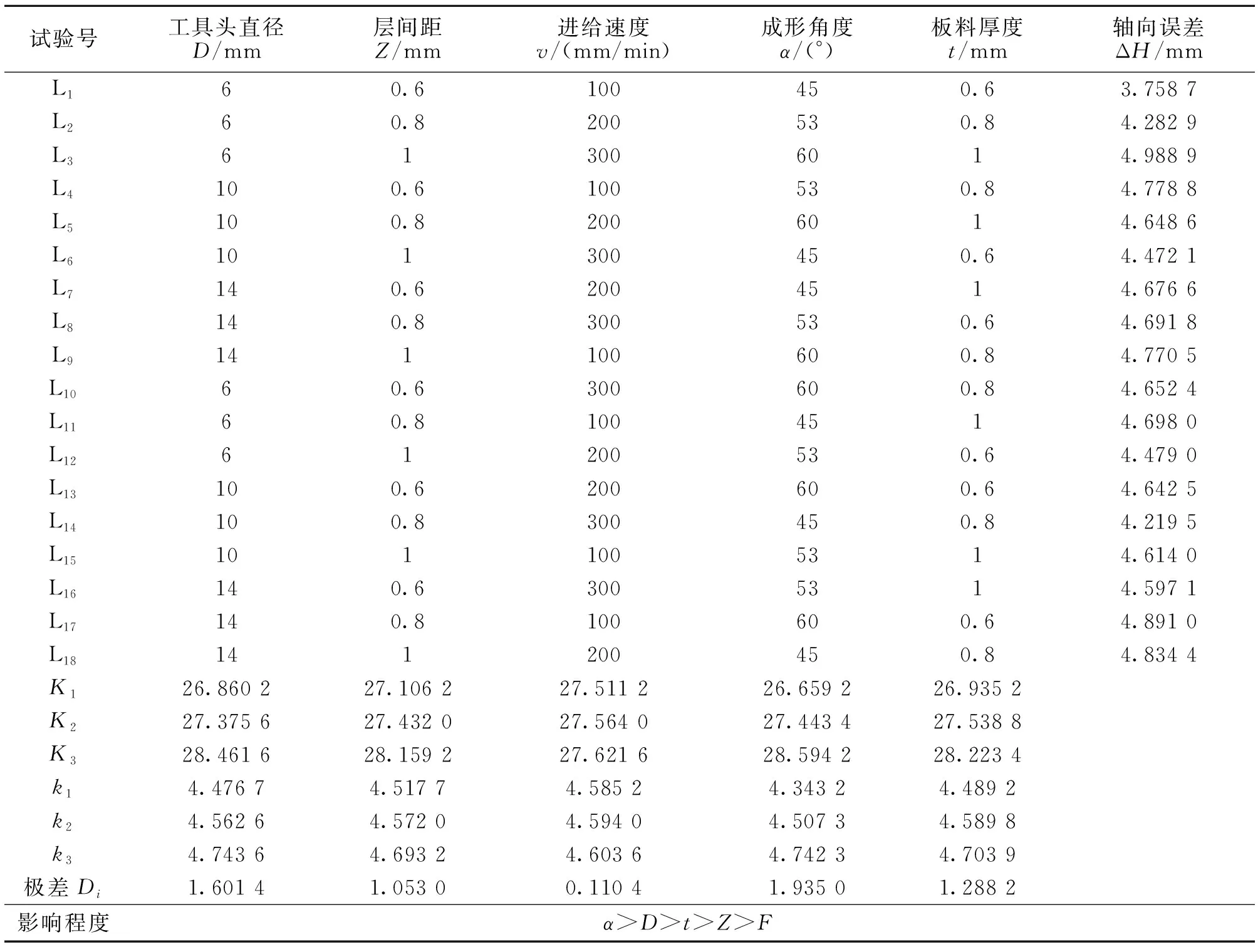
表5 仿真时不同工艺参数对轴向误差的影响Tab.5 Effects of different process parameters on axial error simulation
极差(Di)是将各种因素在每种水平下的模拟结果求和(用Ki表示),用和的最大值减去最小值所得。极差数值越大代表该因素在模拟的水平范围内对结果在数值上影响越大,极差值最大的因素,即为对模拟结果影响最重要的因素。在对轴向误差的模拟中,极差值的大小顺序为:α>D>t>Z>F,故各因素对轴向误差的影响程度从大到小依次为:成形角度(α)、工具头直径(D)、板料厚度(t)、层间距(Z)、进给速度(F)。ki为Ki的平均值(ki=Ki/n),可用来表示每种因素在不同水平下模拟结果的变化规律,即各种工艺参数对成形精度变化规律的影响。
正交实验和单一实验下不同工艺参数对轴向精度的影响规律和影响程度对比见图9。
由图9可以看出,在单一实验和正交实验中,各因素对轴向误差值的影响规律一致。验证了正交实验模拟得出规律的正确性。轴向误差值随工具头直径、层间距、成形角度和板料厚度的增大而增大,进给速度对轴向误差值影响较小。
3.3 成形精度的经验公式拟合
单点增量成形是一个几何非线性和位移非线性的复杂成形过程,成形机理复杂且涉及的工艺参数繁多,要通过定性的分析得出准确的成形误差表达式比较困难。正交实验统计了大量实际可用的数据,故可利用计算机模拟将实验进行数学模型化,通过回归模拟拟合出相应的数学模型,即可得出较为可靠的经验公式。
正交实验的回归方式中应用较广的是线性回归和二次多项式回归两种,二次多项式回归又可分为纯二次多项式回归、交叉二次多项式回归。对于轴向误差进行回归分析,得出经验公式和对应剩余标准差如下。
1) 线性回归公式:
y1= 2.3362+0.0334x1+0.4387x2+0.0001x3+
0.0214x4+0.5367x5
(1)
剩余标准差为SE=0.081 1。
2) 纯二次多项式回归公式:
y2= 5.2157-0.0260x1-0.8993x2+0.0001x3-
(2)
剩余标准差为SE=0.290 8。
3) 交叉二次多项式回归公式:
y3= -2.6181+0.1625x1+5.8889x2-0.0182x3+
0.0599x4+7.5926x5-0.0744x1x2-
0.0004x1x3+0.0018x1x4-0.0579x1x5+
0.0083x2x3-0.0849x2x4-2.2154x2x5+
0.0004x3x4-0.0031x3x5-0.0768x4x5
(3)
剩余标准差为SE=0.146 1。
可看出线性回归公式的剩余标准差最低,显著性最好,为最优回归经验公式。故轴向误差最优求解经验公式为:
εZ= 2.3362+0.0334D+0.4387Z+
0.0001F+0.0214α+0.5367t
(4)

图9 正交实验和单一实验结果对比Fig.9 Comparison of orthogonal experiment and single experiment results
4 实验验证
4.1 轴向精度的测量
成形件的实际高度测量方法见图10,将数控铣床刀具用直径为2 mm的探针替代,以成形件内表面底部为参考面,记录该参考面z方向坐标,手动控制主轴将探针精确定位在起始功能表面处,记录下该平面z方向坐标,通过对两平面z方向坐标值求差即可得到成形件的实际轴向高度。

图10 三坐标测量示意图Fig.10 Sketch map of three-coordinate measurement
4.2 实验结果分析
采用表4中的实验参数并适当增加实验次数进行成形,求取成形件轴向误差,其变化规律见图11。
工具头直径由6 mm增大到14 mm时,轴向误差由16.92%增大到21.42%,变化显著;当层间距由0.6 mm增大到1.0 mm时,轴向误差由18%增大到20.50%,变化明显;当进给速度由100 mm/min增大到300 mm/min时,轴向误差由20.17%增大到21%,变化不明显;当成形角度由45°增大到60°时,轴向误差由20.50%增大到24.42%,变化显著,成形角度是造成轴向误差的最重要因素;当板料厚度由0.6 mm增大到1.0 mm时,轴向误差由19.42%增大到21.96%,变化不大。
4.3 回归公式的验证
式(4)基于仿真的结果,其正确性和实用性还需进一步经实验结果验证。将表4中各工艺参数分别代入成形精度所对应的三种不同的回归经验公式,把计算出的结果与实验结果对比见图12。
从图12可以直观看出,对于轴向误差,实验结果与各种回归公式所求解出的结果不仅分布规律相同,而且偏差量比较接近。
通过对数据分析可得出线性回归公式所求得结果与实验相差7.06%,纯二次回归公式所得结果与实验相差8.73%,交叉二次回归公式所得与实验相差6.4%,与实验所得结果均比较接近。其中交叉二次多项式回归公式最接近实验值,但其剩余标准差为0.146 1,大于线性回归公式的0.081 1,显著性较差,综合显著性和偏差量选取线性回归公式作为最优经验公式。即:
εZ= 2.3362+0.0334D+0.4387Z+
0.0001F+0.0214α+0.5367t

图11 工艺参数对轴向精度的影响Fig.11 Influence of process parameters on the axial accuracy

图12 轴向误差回归公式与实验结果对比示意图Fig.12 Axial error regression formula and experimental results contrast diagram
5 控制轴向精度的方法
由仿真和实验结果均可看出,单点增量成形过程中轴向误差在15%以上,已经严重影响成形件精度,故必须提出能减小轴向误差的方法。通过以上分析可得出采用合理的工艺参数可以在一定程度上控制轴向误差,但提高的程度有限,还不能达到要求的精度。故提出以下两种提高轴向精度的方法。
1) 误差补偿。见图13,将高度补偿区域设定在板料的弯曲变形区域,以理想工件上端面为参考面向上补偿,每向上补偿1 mm,顶圆直径增加2 mm,将通过补偿的成形件沿理想成形件的上端面切割即可得到轴向精度较高的工件。补偿高度与轴向精度的关系见图14(Δh为补偿量)。

图13 轴向几何误差补偿Fig.13 Geometric compensation for axial error
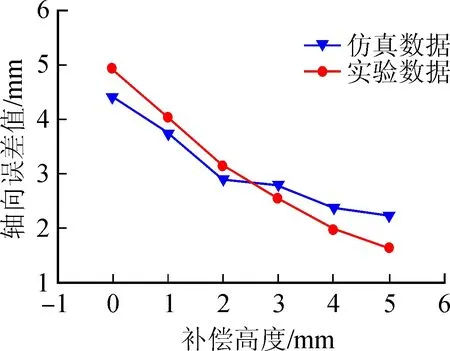
图14 轴向误差与补偿高度关系示意图Fig.14 Diagram of relationship between axial error and compensation height
由图14可以看出,轴向误差与补偿高度基本成线性关系,当补偿高度由0增加到5 mm时,轴向误差由4.920 mm减小到1.632 mm,轴向精度提高了13.71%,轴向精度得到了较大程度上的提高。故增加补偿高度可得到轴向精度较高的成形件。
2) 工具头自转生热。单点增量成形所采用的成形工具头多为球头形刀具,在成形过程中对工具头施加一定转速可使成形区域局部温升,使板料的屈服强度下降,从而提高板料的塑性,减小成形力,达到提高成形精度的目的。在0~2 000 r/min范围内每隔250 r/min进行一次成形实验,测量实验后成形件的轴向误差值,得出转速与轴向误差的关系见图15。

图15 工具头转速与轴向误差的关系Fig.15 Relationship between speed of the tool and axial error
由图15可以看出,当自转转速在0~750 r/min的范围内,轴向误差随工具头的转速的增大而减小,超过750 r/min的范围轴向精度随着转速的提高基本不变,考虑到高转速对机床主轴造成伤害,实际成形过程中选取转速750 r/min,在获得具有较高轴向精度的成形件的同时还可以减小对机床主轴的伤害。
6 结 论
1) 建立了以圆锥台件作为研究对象的仿真模型,并利用此模型研究了层间距、成形角、进给速度、板料厚度以及工具头直径等工艺参数对轴向误差的影响规律,并通过实验对其结果进行了验证。
2) 轴向误差值随着层间距、成形角、进给速度、板料厚度以及工具头直径的增大而增加,成形角度是造成轴向误差的最重要因素。
3) 通过单一实验验证了线性回归公式,可以较好地预测成形件的轴向精度。
4) 采用高度补偿和工具头自转生热的方法可有效减小轴向误差。
