在操作活动中促进儿童数学思维结构化发展
2019-01-17郭文静
郭文静
摘 要:理解思维结构化的前提是先了解小学数学的知识结构,以及小学生的认知结构特点。关注如何促进数学思维结构化的发展,从贴近学生“最近生活区”的生活情境、从体现“现场过程感”的操作活动、从学生间“交流展示、经验分享”中思考。
关键词:认知结构化;思维结构化;操作活动
一、备课思考
(一)关键词界定
《义务教育数学课程标准》中指出:数学教育要发挥数学在培养人的思维能力和创新能力方面的不可替代的作用。所以在培养思维能力的同时,应该关注如何促进数学思维结构化的发展。理解思维结构化的前提是先了解小学数学的知识结构,以及小学生的认知结构特点,从而有目的地促进思维结构化。
小学数学思维结构化是指教师的教学指导,让小学生在学习的过程中去认识其中的关联性,理解知识的逻辑关系,并通过不断学习,不断深入,达到一定的知识积累,进而逐步意识到小学数学知识结构和方法结构的重要性,养成良好的思维习惯,从而形成具有一定数学认知的数学思维结构化系统。
(二)教材结构分析
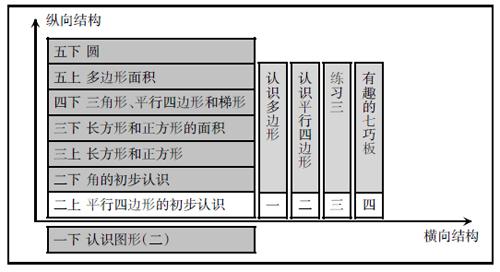
把握纵横结构,使学一单元能见一片,是从外而内的结构理解,到由内而外的创生发展。平面图形从一年级到五年级都有学习,呈螺旋上升趋势。苏教版二年级上册“认识多边形”一课是在一年级认识长方形、正方形、圆和三角形等平面图形的基础上学习的。
本单元第一课时通过从日常生活中常见物体的面上“找出边数相同的图形”等活动,抽象出图形的构成要素“边”的条数,进而认识多边形,是探索和认识平面图形的主要方法。第二课时认识平行四边形,在第一课时初步认识的基础,从不规则的四边形到规则的四边形,研究“普遍”当中的“特殊”性,最后一个活动课延伸到多边形的应用,更具有趣味性和生活性。
二、课例反思
基于对学生认知结构和思维结构化的理解,在分析学情和学理下设计本节课的教学。课例1是以教材为主题,意在整合学生知识结构,从而从“边、点”等多角度理解多边形。课例2是在3×3备课思路的基础上教学,意在以生活中知识经验和思维方式为载体,通过各种活动促进学生思维的进阶,促进数学思维结构化地发展。
(一)“连续”——活动情境贴近学生“最近生活区”
【课例1】
1.情景引入。老师在暑期出游的时候看到了一扇很有意思的窗格。
2.你能找学过的图形?(生指)为了看清楚,老师想把三角形描出来。描的时候注意什么?为什么?(示范描边,三角形,它有三条边。)
3.活动1:窗格中还有什么图形呢?
请你找一找边数相同的两个图形,像这样描一描,说有几条边。(和同桌交流。)
【课例2】
1.你知道哪些图形?
2.看,教室窗户上有什么图形?由几个这样的图形拼成?
天花板上有什么图形?是由多少个正方形拼成的?
3.活动1:找一找生活中有沒有这样用很多图形拼成的图形?
活动2:描一描窗格中有什么图形?
【反思】在课例1中先由教师示范描出已经认识的三角形的边,引导学生学会描图形边的方法并顺势提出“找出边数相同的图形”。正是由于有了认识三角形边的学习环节,为后面找边数相同的四边形、五边形……的学习活动提供了支撑,使学习活动有序、高效。这个课例中是老师主导,创设情境,引导学生围绕一个主线“找出边数相同的图形”去思考,是教师引导下的思维模式。
反观课例2,从学生身边最近的生活入手,让学生感受身边的图形,感受生活中有很多物体是由多个图形拼成的一个大图形,仿佛数学课变成了一节有意思的生活发现。再引导学生主动观察生活中还有没有这样用很多图形拼成的图形。最后在“美丽”的窗格中或者描一描,或者涂一涂不同的图形。在几个学生的分享交流中初步感受多边形是由多条边围成的,体会边数和多边形之间的关系。这个课例是以学生已有认知经验和思维水平为主题,通过“欣赏活动”“找图形”“涂出来”这些活动让学生感受到生活中图形的美、建筑的美,让学生的生活经验有了“质”的提高,让数学的思维有了“美”的提升。
可见,小学生思维发展的基本特点是从以具体形象思维为主要形式逐步过渡到以抽象逻辑思维为主要形式。所以,我们在设计“生活情境”时,要贴近学生“最近生活区”,把握学生的思维发展特点,善于利于生活中的真实工具来辅助教学,让学生多看、多听、多感受,增强感性认识,启发引导学生凭借形象思维来发展初步的逻辑思维。
(二)“关联”——操作活动中体现“现场过程感”
【课例1】
游戏1:围一围。四人小组一人围一个不同边数的图形,围完之后说说你围的是什么图形,有几条边?
小组汇报:你是怎么围四边形的?像这样围一个四边形需要勾住几个钉子?谁是围五边形的呢,需要勾住几个钉子?围六边形呢?
游戏2:画一画、分一分。这是一个四边形,如果用一条线把它分成两个图形,可能是什么?画两个四边形,把一个四边形分成两个三角形。另一个四边形分成一个三角形和一个四边形。
游戏3:剪一剪。正方形纸上剪下一个三角形会是什么图形呢?剪一剪,数一数,作品展示汇报。
【课例2】
活动1:剪一剪,怎么才能将四边形变成五边形?五边形可以变成六边形吗?
活动2:围一围:教师示范围三角形。四人小组每人围一个三角形和一个四边形。
活动3:折一折:将一个长方形对折后是什么图形?这张纸还是四边形吗?
用正方形纸折一折,和同桌交流折成了什么图形?(只能折一次)
学生展示汇报。
【反思】在课例1中教师在最初设计时想让学生在小组里体验不同图形的围法,并通过“勾住几个钉子”感受多边形顶点的特点。但实际教学中实行起来却是很勉强,首先四人小组中学生个体思维水平并不均衡,有的小朋友只能围三角形、正方形,边数越多越不知道该怎么做。其次,学生不理解“勾住”的意思,他们觉得“经过”的钉子也算。所以关于“多边形顶点”的特点解释得很牵强,没有达到孩子的认知水平。教师在设计的时候应该多从学生生理发展和认知发展考虑,而不是刻意让学生思维不切实际地“跳一跳”。
课例2中老师设计的围一围活动就是让四人小组每人围相同边数的图形,让学生体会虽然图形形状不同,但是边数相同,进而思考构成图形的边、顶点和角等要素,深化对多边形的认识。也是在一年级下册围长方形和正方形的思维基础上建立的,将原有的经验运用并结合本节课的知识进行再建构,从围“四边形”到“五边形”到其他“多边形”。将课例1中的分一分和剪一剪的活动合并成折一折,促进学生富有个性地进行操作和思考,有利于学生获得图形变化方面的经验,发展初步的空间思维能力和实践能力。
数学知识体系不是由一个个概念、知识点机械罗列而成的,而是按照知识之间的内在联系组成的逻辑结构系统。教学中教师应让学生在构建模型、建立联系、运用深化等学习过程中使知识系统化、条理化、结构化,从而促进学生结构化思维的发展。
(三)“循环”——学生间“交流展示经验分享”
“展示”是在课堂中将学生作品进行多元的丰富呈现,也可以是正误的比较唤醒,这样能够让学生形成自助与合作的能力。分享是以交流经验的方式方法或者是思想的思维结构,让学生把自己的发现与发明共享给别人。
【课例】我们周围生活中有很多多边形,如教室窗户、地面、地砖、学校的小操场、书橱等。如果让你设计一个由多边形组成的书橱、窗户,或者把你看到的生活中漂亮的多边形画下来,相信一定很有意思。
教师让学生再一次回到生活中的多边形上,联系生活实际画出多边形,体会数学与生活的紧密联系,增强对数学学习的兴趣,感受图形的美,提高审美感受。绘画作品分为生活类多边形和想象类多边形,生活类主要是基于生活中的实物,培养学生主动观察、主动发现的思维能力,将生活中的真实物体和多边形平面图形相结合。想象类主要是用不同的多边形和生活中的人、事、物相结合进行创作,发展学生的想象思维能力和创新思维能力。真正做到用眼睛去发现生活中的多边形,用想象去丰富认识的多边形,让多边形活起来,让多边形贴近生活。
结构化的知识单靠教师的教学、学生的理解是不可能立马就形成结构化思维的。根据学生的认知结构性特点可知,只有大量的知识积累,才能形成一定的结构思维,因而要培养小学生的数学结构化思维,终究还是要靠学生自己的不断练习和积累。
总之,学生在已有数学知识经验结构基础上,借助教師对小学数学教学内容的整体理解与适切的课程开发,经历个性化的“连续”“关联”“循环”的认知转化,在情境中感受真正“贴近生活”的实际意义,在操作活动中感受“实际过程和知识之间”的联系,在同伴间展示自己、交流想法、分享成果,最终促进结构化思维发展,实现心智转换,发展结构化学习。
编辑 王彦清
