基于聚类与SVM短期负荷预测的算法
2019-01-17陈祖成王硕禾赵绍策
陈祖成,王硕禾,王 刚,赵绍策,韩 帅
(石家庄铁道大学 电气与电子工程学院,河北 石家庄 050043)
1 问题提出
企业采用最大需量标准支付基础电价时,如能准确预测峰值负荷出现的时间和强度,采取有效技术手段避免大的峰值负荷的产生,对以电弧炉为主要设备的特钢生产厂家这样的高耗能企业来说,不仅能降低装机容量、节约基础电费开支,而且能够避免对上一级电网造成过大冲击[1]。不少学者对电力度负荷预测做了研究,文献[2]提出了一种相间重构与支持向量机相结合的短期功率预测方法,利用相间重构的方法获取相空间中的数据序列,作为支持向量机的输入,建立负荷预测模型,提高了一定的预测精度,但是效率较低;文献[3]提出采用加权粒子群优化的 LSSVM电力负荷预测,该算法采用加权的粒子群优化传统的LSSVM的参数,并将此模型应用于钢铁企业的电力负荷预测,结合实际条件,选取合理因子,算例分析取得了较好的预测效果,但是对于历史数据的处理做得不精细,存在一定缺陷。
支持向量机(SVM)是统计学习理论中最实用的一部分,主要是针对模式识别问题和统计回归问题。
支持向量机作为一种解决小样本、非线性、高维度数据的拟合问题上有着优良的效果。采用结构化风险最小的原则可以对数据进行全局最优化处理且模型的训练较为容易[4]。在对现场工况和数据进行详细分析的基础上,本文提出首先利用聚类算法对大量源数据进行分析,然后以聚类之后的统计数据经过matlab归一化函数处理后做为输入向量,通过CV判别算法选择具有很好逼近效果的核函数,在输入空间计算出点积。为了有效地消除SVM中的“维数灾难”影响,需要通过非线性变换将原空间转换成高维特征空间中的线性问题,从而建立最优超平面模型,最后利用该模型完成48 h短期负荷预测[5-6]。
2 联合聚类与SVM的短期负荷预测算法实现
SVM是一种适用于小样本数据的机器学习算法。在给定的数据逼近的精度与逼近函数的复杂性之间寻求折中,以获得最好的泛化性能,SVM的基本点是回归。当SVM在实际应用时,需要选择合适的模型,即对选择合适的参数和核函数。
2.1 历史负荷数据的预处理
短期负荷预测需要收集大量的负荷数据,如果不对负荷数据进行预处理势必会造成预测精度的降低,选用合适的数据处理方法尤为重要。历史负荷数据的预处理包括对数据进行补缺和修正,以提高数据质量。本文主要采用以下方法:
1)数据的初始滤波。假设电力系统的历史负荷数据的变化可用下式表示:
(1)

3)数据的补充。电力负荷数据有一定的规律性,根据历史数据的规律,采用聚类的方法选取与缺失数据相似度最高的几个数据求取均值作为补充,提高数据质量。
最后利用归一化函数对电力负荷的历史数据进行归一化,主要目的是消除量纲等其他因素对输入向量的影响,继而使权值调整进入误差平坦区。
2.2 利用聚类算法实现SVM输入向量的确定
聚类是分类问题中一种统计分析方法,也是数据挖掘中的重要算法,是从大量的历史数据中挖掘其潜在价值[7-9]。本文利用分割聚类法(partitioning methods)中的K均值聚类,它是基于距离平方和最小的聚类方法:
1) 假设要聚成K个类,那么首先选择K个初始质心c1,c2,…,ck;

根据划分到每个簇内的点,更新质心,直至质心不在变化。以误差平方和(sum of squared error,SSE)为衡量聚类效果的目标函数,求其最小值,进行全局优化。SSE为:
(2)
式(2)中Ci是第i个簇,x是Ci中的点,ci是x的平均值。对SSE求导,令导数为0,求出第k个质心ck。簇的最小化SSE的最佳质心即为簇中各点的均值。应用中通过有效的数据预处理避免了K均值算法在聚类过程中趋向于无解的情况,提高了输入量的聚类质量,获得较理想的聚类效果。见表1。
通过设置不同的参数和得到的结果,找到了以误差平方和最小值为目标的48点聚类中心,即这48个点同一簇实例之间的距离最小。在聚类过程中,通过比较同一类数据之间的相似程度平滑了负荷序列,经过聚类之后,日负荷数据信息容量大量减少,由原来的1 440组数据压缩成48点数据,解决了样本容量过大而导致的复杂性问题和数据不规范性。最终由聚类的输出确定了支持向量回归模型的输入向量。

表1 日48点中部分点负荷聚类输出结果
2.3 交叉验证评判确定SVM核函数的选择
SVM经常选用线性函数、RBF函数和多项式函数做为内积函数。核函数的形式确定了特征空间,核函数的选择决定了构造分类器空间性质[10]。
对于某一具体问题,选择合适的核函数并没有标准准则。本文提出通过交叉验证算法(CV)来判断确定核函数的选择是否恰当。评价SVM算法的效果通常是通过对比较该算法的泛化能力来完成,小样本数据时,CV是评估分类器泛化残差的一种有效方法,当采用k折交叉验证方法时,训练样本M划分为容量大致相同的k个互不相交的样本,及S=S1∪S2∪S3…Sk,共进行k次训练和测试。
利用算法导入训练及计算出决策函数后,就可以对预测样本Si进行预测,根据不同时段的数据采取不同的核函数进行预测的结果如表2。
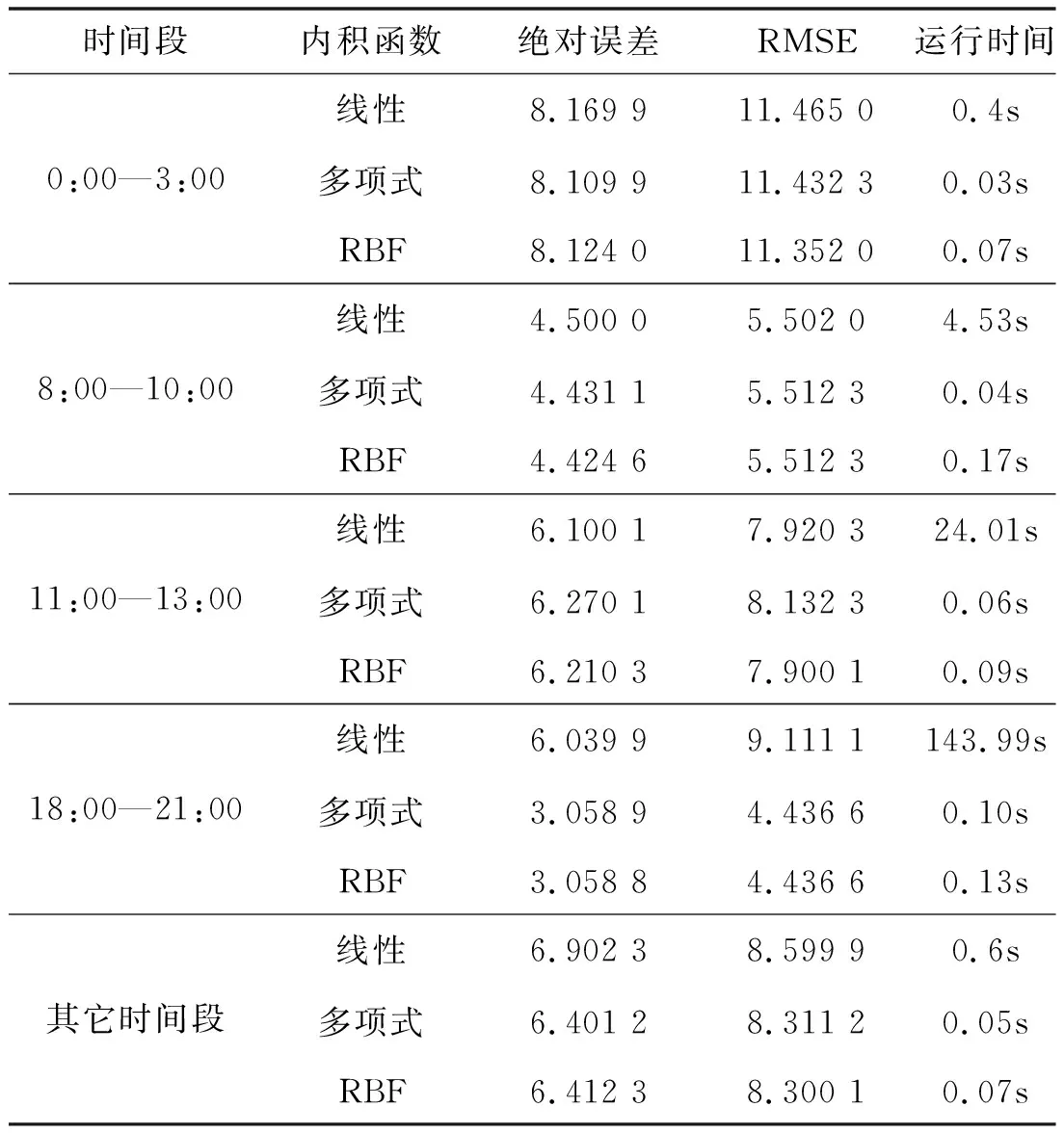
表2 不同内积函数的误差和运行时间结果
比较结果,多项式和径向基核函数的预测效果要好于线性函数,在上午(8:00—10:00)和傍晚(18:00—21:00),多项式和径向基核函数的预测精度基本一致,但是在预测速度上明显是多项式核函数快,所以这两个时段内选择多项式函数作为预测核函数;对于凌晨(0:00—3:00)和中午(11:00—13:00)系统负荷较低的时间段,径向基核函数的预测准确度明显高于多项式核函数,所以在这个时间段内选择径向基核函数作为预测;剩余时间段内,选用径向基核函数可以保证预测速度和精度。
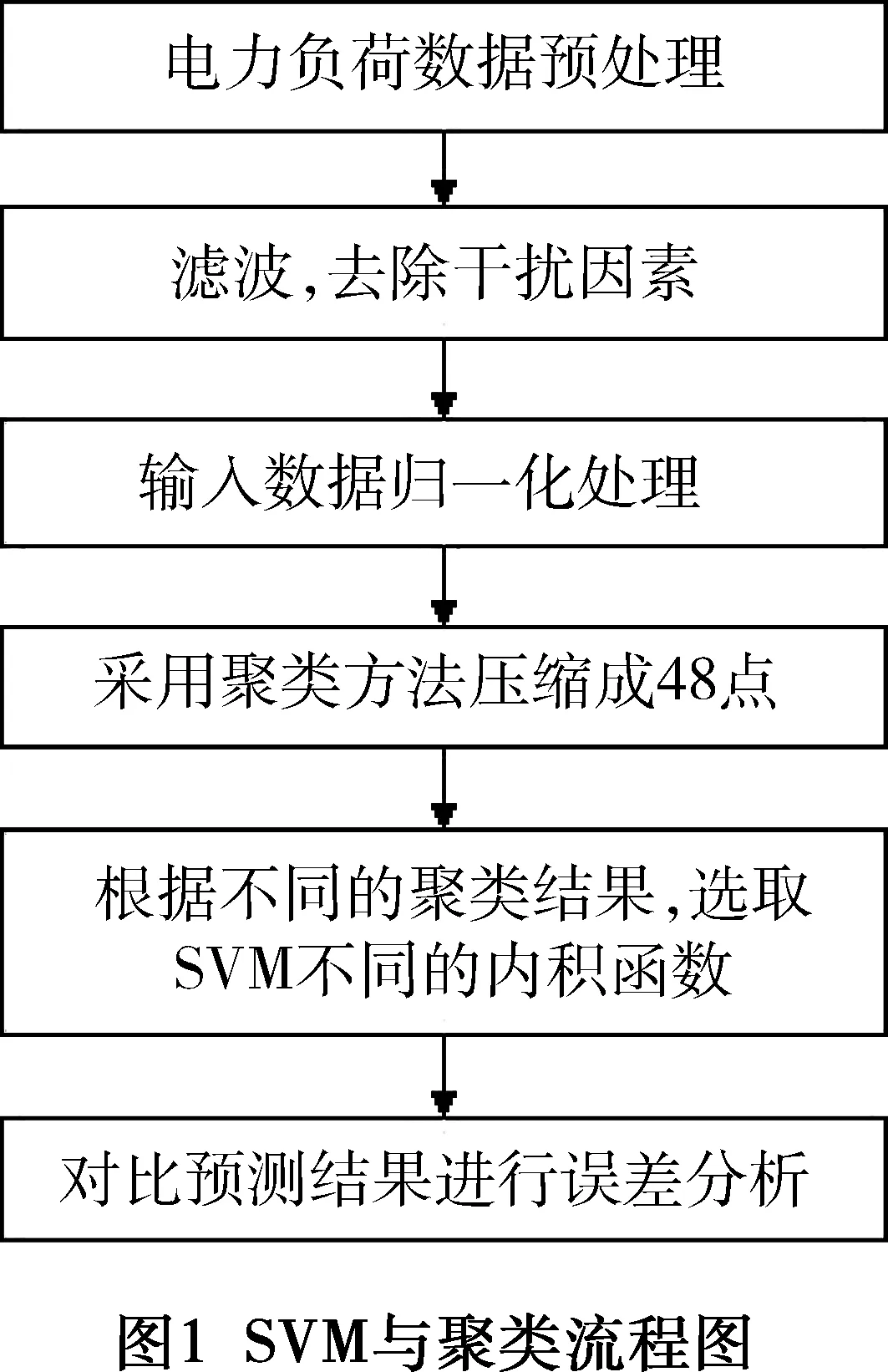
2.4 算例分析与实现
算法的实现框图如图1所示。选择边际系数C、不敏感损失函数中的误差ε以及核函数宽度系数σ2进行SVR回归模型训练,实现步骤如下:
1)拉格朗日乘数取初始值,通常αi=0;
2)首先利用第一个训练样本,计算其KKT互补条件,寻找与KKT互补条件的样本点不相符的拉格朗日乘数,将该乘数作为两个拟优化的拉格朗日乘数之一;
3)由最大优化步数选取在原始样本集中满足max|f(x1)-f(x2)+y1-y2|条件的样本点对应的拉格朗日乘数。保证其余拉格朗日乘数不变,形成一个最小规模的二次规划问题。求解上述问题,得到一对新的α1、α2;
4)样本计算结束,执行下一步,否则返回(2),计算下一样本;
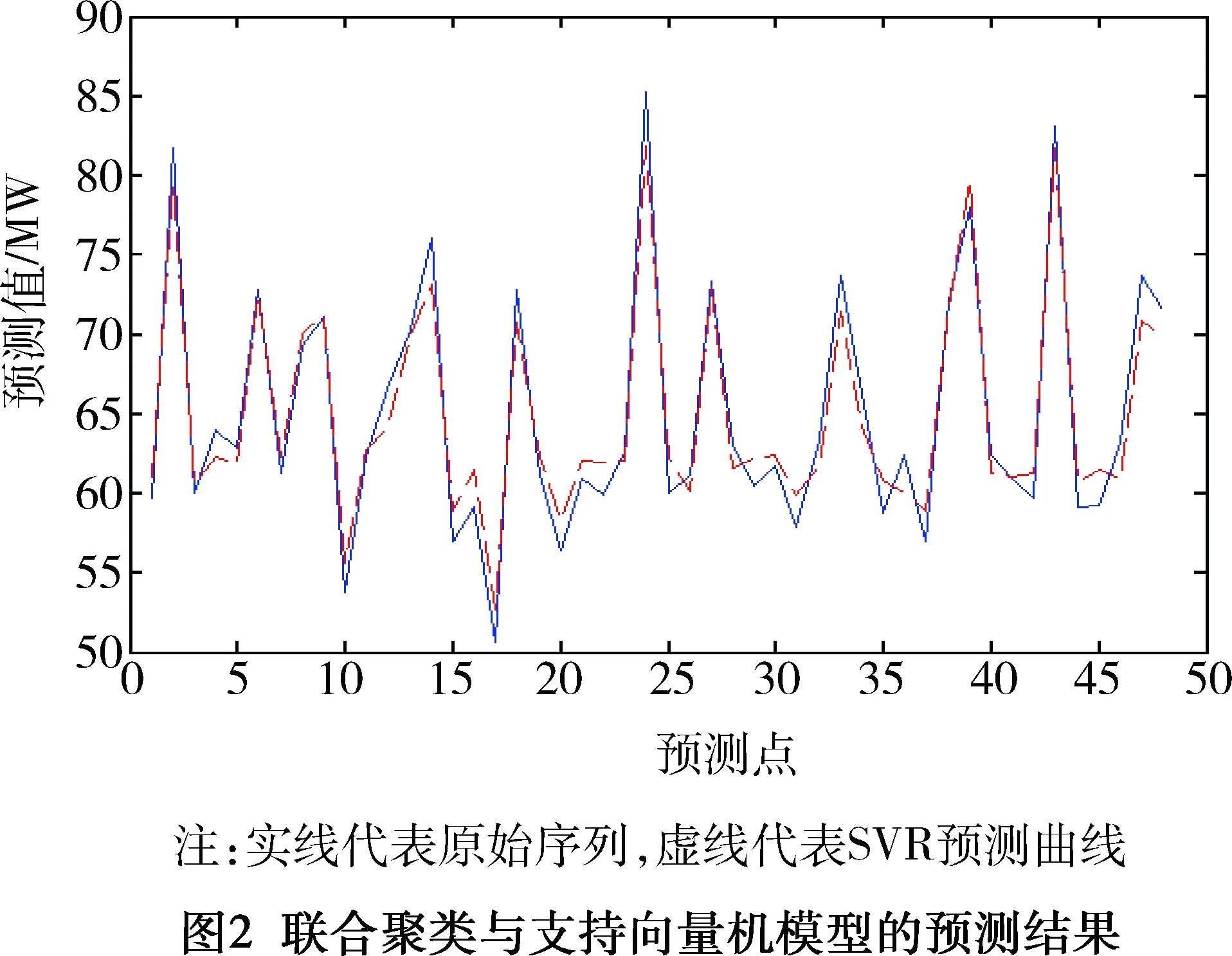
5)将0<αi 待训练完成,在建立模型对样本进行预测,把归一化后的结果与真实值进行比对,能够清晰地比较预测结果。在表3和图2中,分别计算出实际运行系统中每日48点的负荷预测数据与真实数据,相对误差参数等信息,选择部分数据列出在表3。 表3 SVM预测值与真实值的部分数据比较结果 由计算的预测数据可以得出以下结论:1)负荷的波动性对预测结果影响不大;2)预测值与实际负荷结果基本一致,相对误差很小;3)对冲击性负荷的预测效果也很好,最大误差仅为4.11%。所以该算法具有一定的实用价值和研究价值。 SVM在负荷预测研究中经常被用到[11-13]。本文提出了一种基于聚类和支持向量机的短期负荷预测算法,该算法先采用数据挖掘技术中常用的聚类算法对历史数据进行预处理,在确保数据质量的情况下,选取聚类中心作为SVM短期预测模型的特征输入,然后利用交叉验证方法选取合适的SVM内积函数,最终完成负荷预测。结合相关企业的研究背景,收集相应的历史负荷数据,采用该模型进行预测,经过算例分析,发现该算法能够提高电力负荷预测精度,尤其对冲击性负荷,逼近效果也很好;该算法还可以有效地去除数据的异常、缺失和复杂性对预测效果的影响。对AI预测算法,很大程度上取决于训练集,选取合适的训练集可以有效提升预测效果,达到误差范围。
3 结论
