大型精密装配激光定位测量技术研究

王志华，李楠，吕国兵

(北京新立机械有限责任公司 检测校准实验室，北京 100074)

0 引言

在航空航天、重型机械等大型装备制造业中，对大型设备或机械部件精密装配的质量控制越来越严格。开展大型部件精密装配激光定位测量技术研究，是装备目标空间位置解算的重要保障，对于提高大型精密装配精度和效率、积累测量技术经验具有重要意义。

1 传统方式及其遇到的问题

大型部件精密装配通常以传统专用工装作为辅助，并配合利用基本物理原理来实现一些复杂的装配测量。例如，在大型车辆精密装配过程中，如何精确构建车辆中心面装配基准线一直是一项难题，目前一般采用专用工装拉线法配合精密经纬仪来实现装配基准线的定位构建，如图1所示。

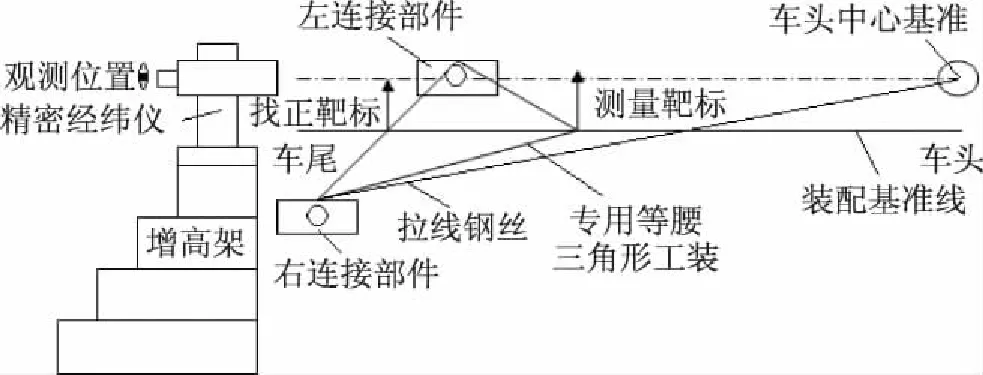
图1 大型车辆装配基准线定位构建示意简图

左、右连接部件为大型车辆装配的重要部件，其左、右轴孔连线与车辆装配基准线在设计上有严格的垂直度要求。图1中采用专用等腰三角形工装，两底角以轴孔为基准，固定左、右连接部件于车尾设计位置，留置测量接口，车头中心基准与左或右连接部件测量接口以细钢丝连接，并用重锤拉直，保证左连接部件测量接口拉直的钢丝长度与右连接部件测量接口拉直的钢丝长度相等，即左、右拉直钢丝(两腰)与左、右轴孔连线(底边)形成了等腰三角形，则左、右轴孔连线(底边)中点与车头中心基准的连线必然垂直于底边，可认为装配位置符合要求。之后采用精密经纬仪测量专用等腰三角形工装上相应靶标偏移的角度，并换算成垂直度。如果垂直度满足设计指标，则进入下一步工序，否则调试后再进行同样的测量，直至合格。

左、右连接部件装配位置检测合格并固定后，参照左右连接部件对称中心与车头中心基准的连线，以拉直的细钢丝模拟车辆装配基准线，作为后续设备、零部件等上装时的参考基准。但是，采用钢丝拉线悬挂重锤较为原始落后，调试过程繁琐，不利于提高装配效率；同时，以钢丝拉线法模拟的装配基准线不够稳定，受人为因素干扰较大，且存在直线度误差，对装配精度有着显著影响。为解决以上问题，本文将激光定位测量技术应用于大型精密装配中，以提升装配的准确性和可靠性。

2 激光定位测量技术原理

采用激光定位测量技术，以激光测距定位装置确定左、右连接部件的精确位置，再利用激光标线装置精确构建装配基准线，如图2所示。

左、右连接部件采用专用等腰三角形工装固定在车辆车体尾部设计位置，激光测距定位装置分别安装在专用等腰三角形工装底部的对称位置，确保左、右测量接口连线BC与左、右轴孔连线MN平行。车头中心基准位于车体中心线上。BP连线和CP连线为激光测距定位装置所发射的激光线，照射到车头中心基准位置的激光线经过反射、接收、计时及计算即可实现距离测量。装配左、右连接部件时，通过调节专用等腰三角形工装的位置，使其两侧的激光测距定位装置所测距离相等(在误差允许范围之内)，即图中BP等于CP，由于BC与MN平行，则车头中心基准P与左、右轴孔连线中点O的连线PO垂直于MN，可以认为左、右连接部件装配到位。

图2 激光定位测量系统原理图

图2中EFHG为激光标线装置所发射的扇面激光，并投影于车辆车体上，可精密调整激光标线装置三维调节平台，使其发射的扇面激光精准投影于车体中心线上，形成装配参考基准线(即图2中的投影线EF)。由于扇面激光垂直照射到障碍物时显示为投影线，因此车体中心线上所有接触激光线的物体表面均可显示投影线，这恰好是装配中心线应该具有的功能。使用此方法实际装配时，操作方便、不受环境干扰、不占空间，且准确度更高。可见，以激光定位测量技术构建的装配基准线完全满足装配要求。

3 数学模型

图2中的专用等腰三角形工装在制作时，其顶角A和两底角对称中心D分别安装精密靶标，精密靶标连线AD与底边BC严格垂直(垂直度误差相对较小，可以忽略不计)。

如图3所示，专用等腰三角形工装的两底角B和C分别安装参数完全相同的激光测距定位装置，测量车头中心基准P至左连接部件B与P至右连接部件C的距离。在左、右连接部件精密装配定位过程中，工艺上要求PB与PC距离严格相等，这样PD将严格垂直于BC，那将完全满足设计要求。但是，由于激光测距定位装置存在允许误差限，其安装位置以及专用等腰三角形工装本身也存在一定的误差，因此在装配过程中使其所测数值完全一致有一定困难，从提高装配效率来说也非常不现实，所以装配过程中PB与PC客观上一定会出现距离误差。只要出现距离误差，原理上专用等腰三角形工装必然出现了偏移，即顶角A偏移至A1。

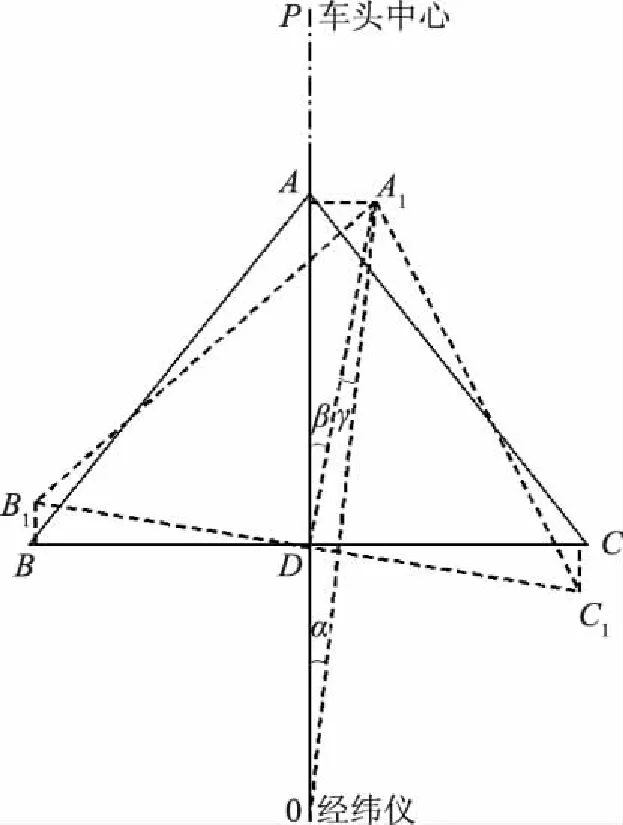
图3 激光定位数学模型依据图

从图3可以得出，实际装配定位过程中，只要测量出图中的偏移角α，即可判定左、右连接部件是否装配到位。精密经纬仪放置在车辆尾部一定距离的O点，平移和调焦使O，D，P三点在一条直线上，观测A1点的偏移角α，可引入设计指标来具体推导，如图3中的虚线图所示，假设DA1=L，DB1=DC1=R，BB1=CC1=δ，OD=d。∠AOA1=α，∠ADA1=β，∠OA1D=γ，其中L，R，d均为已知参数，δ为图纸给定设计公差，根据正弦定理，可得

(1)

根据三角函数关系可推出方程组

(2)

解此方程组可得

(3)

则

(4)

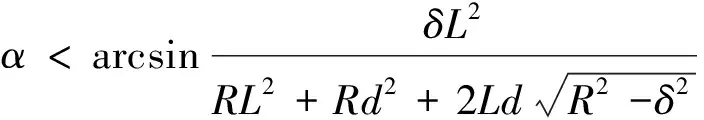
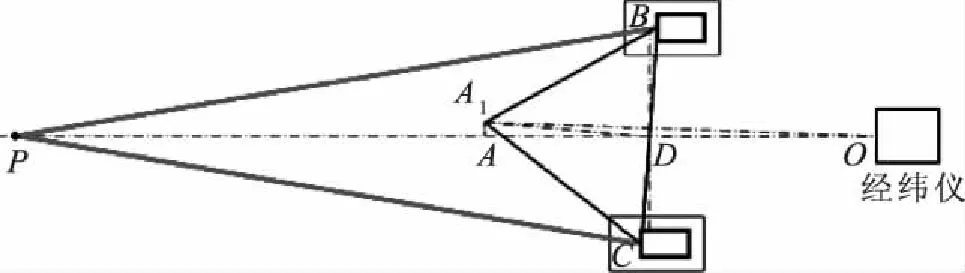
图4 激光定位测量系统实际装配简图

因此，今后在进行大型车辆装配时，只要能保证激光测距定位装置数据准确可靠，便可以安全阈值法调整测量距离差，可以不用精密经纬仪进行测量验证，节约了测量时间，提升了测量效率。

4 大型车辆定位精度评估与比对

为了定量评估大型车辆激光定位测量系统的定位精度，引入具体数据进行分析。代入各已知参数的值：L=1000 mm，R=1000 mm，d=2000 mm，下文将对定位精度进行具体评价。

根据激光测距定位装置的校准证书可知，在20 m范围内，其示值误差最大为1 mm。考虑极限情况，假设两台激光测距定位装置所测距离的误差为1 mm，可认为图4中PB和PC的距离差为1 mm，理想情况下取中值，则PB和PC长度误差分别为0.5 mm和-0.5 mm。此时在图3中，相当于直线BC产生了旋转，变成了直线B1C1，此时取β=β′，δ=δ′。

传统钢丝拉线悬挂重锤的方法引入的误差包括钢丝拉伸变形引起的距离误差、自重引起弯曲产生的距离误差和标记人眼读数误差，依据多次测量经验值应不大于2 mm，可按极限值2 mm估计，理想情况下取中值，则PB和PC长度误差分别为1 mm和-1 mm。

参照上述计算方法，将δ″=1 mm代入式(4)可得α″=22.9″。

上述计算的偏移角α′和α″分别代表了激光定位法和传统钢丝拉线法对大型车辆装配测量定位时的最低极限误差，经试验验证符合实际。从数据可见，激光定位法将最低极限误差减少了几乎一半，而且能以安全阈值法快速调整测量距离差，在满足设计要求的前提下优化了工艺流程，节约了装配测量时间。而传统钢丝拉线法引入的三种主要误差无法消除且不可控，尤其是标记人眼读数误差因人而异，因此每次的测量定位误差评估数据都可能出现较大的变化，无法寻找规律，且每次测量定位都需要较长时间调整钢丝拉线的距离差，装配测量定位效率低下。

可见，以大型车辆精密装配激光定位数学模型为依据建立的方法测量效率更高且准确性更好，定位时读数以数字方式实时显示，方便快捷，减轻了测量工作人员的劳动强度，优于传统钢丝拉线法。

5 大型车辆精密装配基准线的建立

采用前文所述方法可以精确固定左、右连接部件于大型车辆车尾设计位置，之后通过工艺方法很容易找出其对称中心点(即精密靶标D的中心)，使之与车头中心基准连接，形成装配基准线。但该装配基准线是虚拟基准线，传统方法是以拉线法模拟该虚拟基准线。采用激光定位测量系统中的扇面激光标线装置，可直接将该虚拟基准线以投影实线的形式表现出来，以便在后续相关部件装配中直接应用。

扇面激光标线装置的核心部件为激光发生器和大地垂直仪，可以发射垂直于大地的扇面激光，遇到障碍物时投影为直线。采用扇面激光标线装置发射竖直扇面激光，垂直投射到调平的车体上，形成垂直于车体的竖直中心面，并在车体表面形成清晰的细激光线，通过调整扇面激光标线装置的三维调节平台，可以使细激光线精确地重合于车头中心基准与车尾左、右连接部件对称中心上，此时投射在车体上的细激光线正好是装配虚拟基准线的实体表现形式，因此可以直接作为装配基准线。

由于车辆经水平仪调节平行于大地，扇面激光标线装置发射的扇面激光垂直于车体表面，对于车体表面凸出部位(高)和凹陷部位(低)均能投影出细激光线来，显然，这才是激光投影装配基准线的关键所在，其使后续部件在车体高、低部位的装配变得简单，可以直接以激光投影线作为参考基准来装配后续相关部件，传统的拉线法对高、低部位的装配使用悬挂铅锤的方式进行，不仅装配时间长，而且稳定性差、误差大。可见，以扇面激光标线装置产生激光投影线的方法引入误差较小、测量效率更高，且不受人为因素干扰，工艺上更先进，完全优于传统的拉线法。

6 结束语

将激光测距定位装置纳入计量管理，送计量机构定期校准后使用。每次大型车辆左、右连接部件装配时，直接调试专用等腰三角形工装使两台激光测距定位装置所测距离小于安全阈值|Δ|min，则左、右连接部件装配到位，进入下一步工序激光标线装置投影建立装配基准线。可见，其意义在于装配与检测同步完成，不需要事后用精密经纬仪测量偏移角验证，极大地简化了操作流程。

综上所述，激光定位测量技术的应用大幅提升了大型车辆的装配效率及装配准确性，其中激光测距技术和激光标线技术的应用对于大型装配具有重要意义。