基于MATLAB的PDV系统数据处理算法与实现
2019-01-17房文涵
房文涵
(航空工业北京长城计量测试技术研究所,北京 100095)
0 引言
光子多普勒测振仪是利用激光多普勒效应对物体振动进行测量的一种测量仪器。它与传统激光测振仪相比,具有可以远距离测量、分辨力高、测量时间短、抗干扰能力强、响应频带宽等优点,在特殊结构振动物体和复杂环境的测量方面受到重视[1]。
理想的多普勒信号与被测物体的运动速度呈线性关系。光子多普勒振动测量得到的信号,其幅度和频率都随时间变化而变化,是非理想的多普勒信号。这个原始信号受到很多因素的影响,例如光纤器件、被测物体等。所以要想从这些非理想信号中提取出有用的振动信息,必须同时满足实时性、精度、测速范围的要求,这无疑对PDV系统的信号处理技术提出了很高的要求。
1 原理及算法
1.1 条纹法
当运动物体和光源发生相对运动的时候,从运动物体表面反射回来的光会产生多普勒频移。光源发出频率为f1的光波,被测物体的运动速度为u,当入射光垂直打在被测物体表面时,被测物体接受到的频率为F1;接着被测物体当作发射源,在它的垂直向有一个接收体,接收到的频率为F2。此时被测物体的运动速度u表示为
(1)
(2)
只要能找出差频频率Δf,就可以计算出被测物体的运动速度u。差频信号的每一个周期对应一个条纹。找到条纹的相邻极大值(或极小值)对应的时间后,那么其时间差就是差频周期Tbeat(t),根据Δf=1/Tbeat(t),那么差频频率就得到了。代入式(2)可得
(3)
这种方法就是条纹法,即通过计算条纹的周期来计算被测物体的运动速度,进而求出被测物体的振动信息。由以上公式可以看出,条纹法求被测物体运动速度的关键是要精确地求出每个信号极值点所对应的时间。
1.2 PDV系统测振原理
光子多普勒速度测量系统原理如图1所示。半导体激光器发出激光,进入环形器的1端口,2端口与自聚焦棒相连作为检测系统的探头,3端口与探测器相连,并通过传输线与示波器相连,探测器是系统的光电转化部分,示波器作为检测结果的观察显示部分。激光在自聚焦棒的端面上,不可能完全透射,必将有一部分反射回来,将这路自聚焦棒的端面反射光称为一次反射光,将透过自聚焦棒后打在靶体上反射回来的光,称为二次反射光[6]。两次反射的光将会发生干涉,并在探测器上实现光电转化,转化后的信号通过示波器进行观察。

图1 PDV系统测振原理图
在PDV系统中,利用探测器的平方检测特性来提取差频信号,探测器中的光强I为
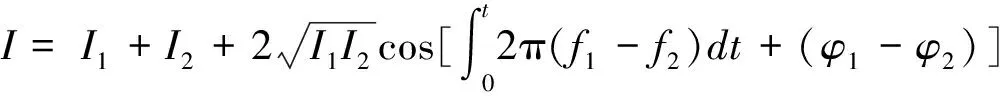
(4)
式中:I1和I2分别为参考光和传感光的光强,若采用交流探测器探测,从探测器输出端到达示波器的电压信号应为
(5)
式中:R为探测器的电压灵敏度。在式(5)中,对由运动引起的相位变化除以2π并取其整数部分,就得到示波器上显示的周期数(条纹数)N,即
(6)
式中:Int表示取整。对式(6)两边求导,可得物体的运动速度与条纹数随时间变化率的关系为
(7)
式中:τ(t)为示波器显示的干涉周期。实验分析得到的关系式(7)与理论分析中的式(3)对应,因此只要确定τ(t),就可以计算出物体的运动速度,进而可计算出运动位移、加速度及振动的频率、振幅等物理量。
1.3 数据处理原理及算法实现
光子多普勒振动测量得到的多普勒信号是一个相对比较复杂的信号,它并不是连续的信号,其具体波形取决于流速场中散射粒子的大小、浓度以及通过测量体的位置;多普勒信号的频率一般都较高,通常在千赫兹的量级上;多普勒信号的信噪比随测量对象而变化,速度越高,信噪比越低[2]。
光电探测器接收的是粒子散射光,其强度本身就比较微弱,而且信号受到诸如光路系统、杂散光、光检测器件噪声影响;当用一般的光子多普勒测振仪检测运动物体时,得到的原始多普勒信号都存在一定程度的噪声及其他误差干扰信号。误差引起的干扰信号可根据理论公式等进行部分补偿修正[3]。而对于高频噪声和高频信号相互混叠的含噪信号或者非平稳信号的消噪,采用小波变换去噪会有很好的效果。这是因为,噪声是一种在时域和频域上能量分布都比较均匀的信号,经小波变换后其频谱图中不会出现特别大的突出峰;而多普勒信号的能量则非常集中,故在信号到达时刻和所在频率段,信号的能量将有一个突变,在频谱上有尖峰突起。
小波去噪算法可以多尺度的分解初始信号,准确找到原始信号的高频成分和低频成分,减少对原始信号的影响,最大可能地去除噪声[4]。对含噪声的信号多尺度分解后,再对各个尺度上的小波系统进行去噪,获得小波逆变换重构函数,最终得到去噪后的有效信号。
小波阈值去噪法是针对噪声的小波系数幅值较小的特点,通过选择合适的阈值来抑制噪声,且保留反映原始的特征尖峰点。该方法计算量小、速度快、适用性广。小波去噪一般有三种方法,分别是强制去噪声法、默认阈值去噪声法、给定阈值去噪声法[5]。其中,强制去噪声法将小波分解结构中的高频系数全部置为0,滤掉所有高频信号部分,然后对信号进行小波重构。这种方法较简单,且去噪后的信号曲线相对平滑,但容易丢失有用部分的信号;默认阈值去噪声法,是利用小波函数生成信号的默认阀值,但这个阈值是不确定的;给定阈值去噪声法,其阀值可在实际去噪过程中通过实验公式获得,比默认阀值的可信度高。
在此基础上,本文提出了一种速度快、可靠性好的数据处理算法。下面对该算法进行详细描述:
首先对获得的多普勒信号进行移动均值平滑处理,通过设置合适的平滑度参数,在保留有效的振动信息的同时,滤掉噪声信号。同时,标出各个时刻平滑后信号的最大值,拟合成曲线,用不同颜色标出。移动均值滤波的原理是,设置平滑度参数k1,k1个数值一组组取平均值,多普勒信号中正反向曲线带有的噪声就可被消除。示波器采集到的原始信号见图2。当平滑度参数过大时,有效多普勒信号会被部分滤掉,即如图3所示的密集曲线处显示大片空白;当平滑度参数过小时,多普勒信号中的大部分噪声仍存在,即如图4所示的多普勒曲线上仍叠加有尖刺。只有平滑度参数大小合适时,信号中的大部分噪声被滤掉,且有效的信息仍被保留,各时刻信号最大值可连成平滑的半正弦弧线,如图5中的绿色曲线所示。
然后,根据标出的各个相邻最大值所对应的时间,求出差频频率Δf,代入式(2)得到初步的速度时间曲线,但在速度曲线的最低点处有少量的尖刺杂峰,见图6。

图2 示波器采集的原始信号图

图3 过大平滑度参数的滤波曲线图
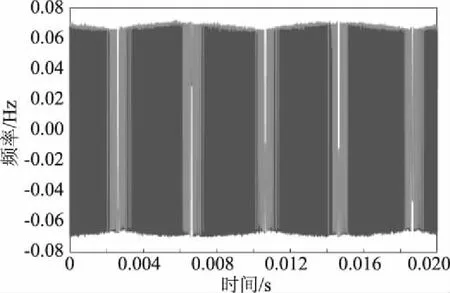
图4 过小平滑度参数的滤波曲线图

图5 合适平滑度参数的滤波曲线图

图6 初步速度时间曲线
这时,需要调整极小限定值与极大限定值这两个参数,找到杂峰的起始点和结束点,如图7所示,将起始点标为绿色,结束点标为黑色。消去杂峰起始点(绿点)到杂峰结束点(黑点)之间的数据,即可去掉杂峰。
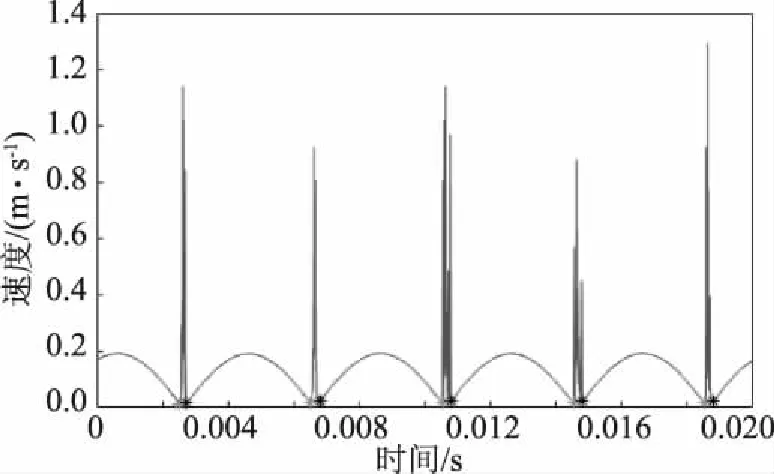
图7 找出杂峰起始和结束点
去掉杂峰后,得到一系列不连续的半正弦曲线,将这些曲线进行翻转及最小二乘拟合处理,获得连续的正弦速度时间曲线,见图8,该曲线直观显示被测物体的振动信息。
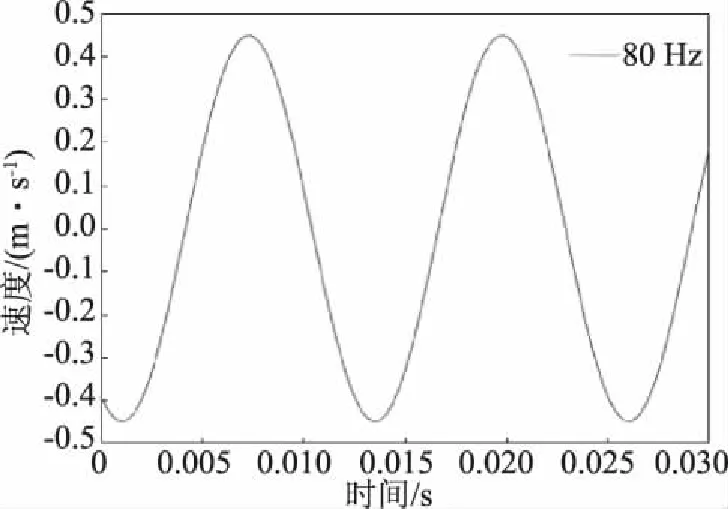
图8 连续的正弦速度时间曲线
2 编程实现
MATLAB具有非常强的数据分析能力,可对数据进行小波变换处理。该PDV数据处理软件操作便捷,其数据处理过程如图9所示。

图9 数据处理程序流程图
1)数据读取
数据读取部分,利用示波器采样,示波器的输出文件为csv格式,则选用数据文件读取函数csvread来读取全部数据。
2)数据初步处理:滤波、平滑等
选用MATLAB中的smooth(I,k1,′loess′)给定阈值去噪声法来进行数据的平滑处理。smooth为移动平均滤波,其默认对数据周围的5个数据点做移动平均处理;k1是平滑度参数,可对指定k1个数据进行移动平均滤波;smooth有5个特定的平滑方法,loess方式是加权的线性最小二乘滤波方式。smooth平滑算法数据处理速度快,实时性好。通过设置合适的平滑度参数,在保留有效的振动信息的同时,滤掉噪声信号。
3)五点法处理得到原始速度曲线
经过初步的平滑滤波后,得到原始速度曲线,只有速度最低点处仍存在杂峰。根据在每五个点中找到其中最大最小值,调整极小限定值k2与极大限定值k3这两个参数,使极小限定值k2的值小于所有的最小值,极大限定值k3的值大于所有的最大值。此时,极小限定值k2和极大限定值k3的值即为杂峰的起始点和结束点[7];将杂峰的起始点和结束点对应的时间段清零,即可消去起始点和结束点之间的数据,去除杂峰,得到一系列不连续的半正弦曲线[8]。最后将这些曲线进行翻转及最小二乘拟合处理,获得最终的连续正弦曲线。
4)速度加速度曲线等参量的显示和存储
利用函数uiputfile({′*.jpg′,′figure type(*.jpg)′},可将得到的速度时间图与加速度时间图,存为jpg格式图片。利用函数uiputfile({′*.xls′,′excel(*.xls)′},可将得到的速度时间数据与加速度时间数据,存为xls格式文件。
3 实验验证
为了测试数据处理软件的稳定、可靠以及普适性,选取激振台作为运动物体,进行测试实验。振动平台由信号发生器、功率放大器还有激振台组成,激振台随着信号的输入发生振动,振动的频率和信号的频率相同,振动的强度和信号的强度有关,即振动强度和功率放大器所选择的放大倍数有关。
信号发生器产生一个固定频率的正弦信号,经功率放大器给激振台一个稳定的正弦电压信号驱动,使钢质的振子做恒定上下往复运动。分别给激振台20,80,160,1000 Hz的正弦信号,让测速系统对其进行检测,通过示波器收集数据,用处理软件处理数据;并且与经校准的激光测振仪的检测结果进行对比,见图10。

图10 标准激光干涉测速系统对比实验
具体操作为:PDV系统与经校准的激光测振仪分别对同一点进行振动测量,求经该软件处理得到的振动频率和标准激光干涉仪解调出的振动频率的相对偏差,是否在实验室规定偏差范围内,来验证数据处理软件的稳定、可靠以及普适性。
不同频率输入信号下的参数及结果如下表1所示。将经校准的激光测振仪解调出的振动频率设为标准频率。光子多普勒测振系统的一般测量精度约为5%,经校准的激光测振仪精度为0.05%,则两者对实验允差可看作5%。
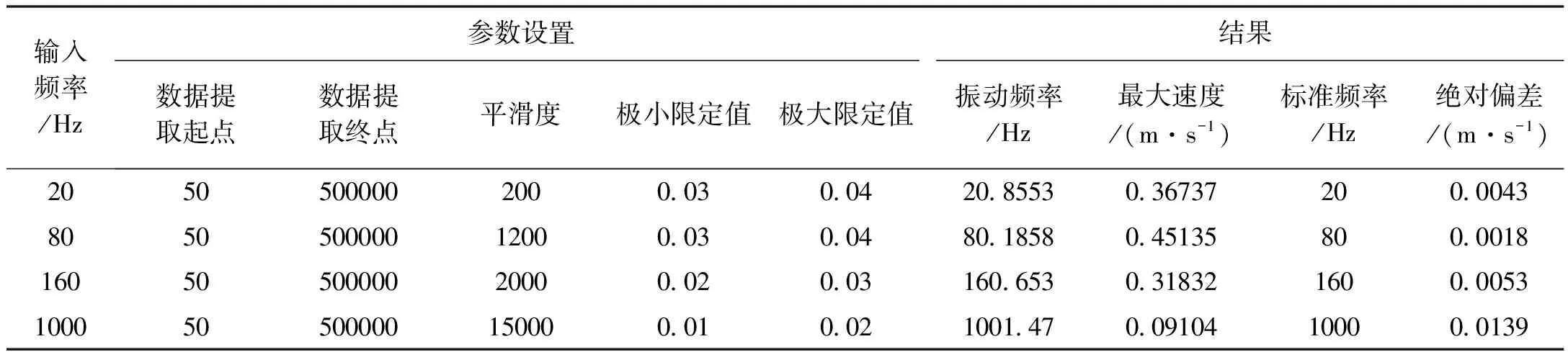
表1 不同频率下解调结果偏差
不同频率输入信号解调后得到的速度时间曲线如图11所示。

图11 不同频率信号的速度曲线图
根据表1中的实验数据及得到的速度时间曲线,可以发现:经该数据处理软件处理得到的振动频率与经校准的激光测振仪解调得到的振动频率的偏差很小,在对比实验的允差范围内。数据处理的频率范围是20 Hz~1 kHz。故本数据处理软件算法稳定、可靠、便捷且具有普适性。
4 总结
在条纹法基础上,利用MATLAB小波函数smooth给定阈值去噪声法实现了对PDV系统多普勒信号的去噪平滑处理,得到了理想的正弦信号曲线。经过激振台的测试试验,PDV数据处理软件能正确地显示并计算出物体速度变化,具有良好的可靠性。
