中国的经济规模被高估了吗？——基于地下经济的反证

王永兴

一、引 言

自2018年1月起，中国内蒙古自治区和天津市先后大幅核减地方GDP，掀起了主动“挤水分”的序幕，这一变化再次引起了国内外对中国经济增长真实性的广泛关注。改革开放四十年来，伴随着中国经济的超高速增长，国内外学术界对中国经济增长真实性的质疑不绝于耳。如世界银行（1997）认为中国 1978—1995年的经济增速应下调 1.7个百分点。Young（2000）认为中国三次产业的隐形缩减指数系统性地低估了物价变动，通过重新调整得到的计算结果显示中国在 1978—1998年的经济增速被高估1.7个百分点。孟连和王小鲁（2000）也通过对价格指数计算方法、工业实物量、货物数据的分析得到了类似结论。Ramski（2001）则从数据不一致、数据渠道单一和旅客周转量三个方面论证了中国的GDP高估问题。较近的质疑来自伍晓鹰（2014），他认为中国1978—2012年的 GDP平均实际增长仅为 7.2%，远低于官方公布数据。针对以上质疑，张新（2002）、许宪春（2015）等学者已经分别从第三产业漏报、租金数据缺失、GDP平减方法可靠性等方面进行了反驳。不同于以上研究，本文拟从地下经济这一全新视角对中国经济增长的真实性问题进行论证。地下经济是指游离于国家统计体系之外的经济活动，因此其规模越大，意味着官方 GDP水平低估程度越高。在我国进入全面深化改革阶段的大背景下，探究中国经济增长的真实性问题尤为重要。真实经济规模的掌握有助于优化调控效果、提高宏观调控能力，任何经济政策的制定都需要一系列的宏微观经济数据作为参考，无论高估还是低估经济规模都会极大地增加经济政策制定过程中的误判几率。

本文的贡献体现在以下几个方面：首先，相对于同类研究更好地处理了“基准值”设定问题，从而提高了结果的可靠性；其次，引入了更多的指标变量进入基础模型，在此基础上进行竞争性筛选，减少了设定失误的风险；再次，从实践意义上看，本文的实证结果为探究中国经济增长的真实性问题提供了一个新的视角，从而有助于更全面、客观地观察中国经济发展。

本文余下部分安排如下：第二部分对相关文献进行梳理，并对地下经济的规模估测方法进行比较；第三部分对模型指标选取的依据和采用的基本技术路线进行说明；第四部分对本文的数据进行描述性统计，并说明其具体来源；第五部分结合中国宏观经济数据使用模型进行估算；最后是对本文研究局限的总结以及对该领域未来可能发展方向的展望。

二、文献综述

国外对地下经济问题的研究最早可追溯至 20世纪 70年代，时至今日，其研究重心仍集中于对各国地下经济规模进行定量估测。我国对地下经济规模估测的研究工作始于 1999年，梁朋和梁云（1999）首次使用 Gutmann（1977）设计的货币需求方程模型（简单现金比率模型）估算了中国 1985—1995年的地下经济规模，这项研究成果标志着我国国内学者在这一领域开始与国际主流方法正式接轨。该文的局限是，尽管已经清晰地意识到了现金比率模型的假设条件存在局限，但在技术上未进行细致讨论和作出相应调整。此后，很多国内学者开始直接套用 Tanzi（1983）、Feige（1986）等发展的货币模型来研究中国的地下经济规模，由于篇幅所限，我们对此类研究得到的详细结论不再赘述。与此同时，国内也有很多学者在原始模型的基础上不断深入探索，做出了不同程度的创新。

朱小斌和杨缅昆（2000）把地下经济分为“浮现地下 GDP”与“流通地下 GDP”两个部分，该文对“流通中现金”的范围作了进一步细化，具有一定的创新性。夏南新（2000）放松了现金比率模型的关键假定，并对这些假定的可能影响方向做出了预测，但在实际估算中仅对地下经济中的“现金-活期存款”比率（Ku）进行了放松，并未对所有的假设均进行验证。此后，夏南新（2004）又根据中国国情对 Tanzi模型中的货币需求方程进行了修正，加入了零售价格指数等控制变量，同时他还发现利率变量对中国货币需求的影响并不显著。罗磊（2005）也认识到现金比率模型的假设条件与现实存在差异，但仅对第一个条件进行了放松，允许官方“现金-存款”比率随各自增长率变动，并未对其他假设进行调整。针对同一问题，刘华、张伟伟和廖福刚（2007）采取的方法是分别用现金和存款变量对时间变量进行回归，进而推导官方“现金-存款”的比率，但他们对地下经济中的“现金-活期存款”比率（Ku）的处理过于简单，同时也保留了正规经济与地下经济货币流通速度相同的假设。王永兴（2010）对现金比率模型的三个假设条件均进行了放松，讨论了不同情况下放松假设对估测结果影响的方向（提高或降低），他注意到 Acharya（1984）和 Feige（1986）等学者对原始 Tanzi模型的各种批评，并根据我国的实际情况对货币方程模型的解释变量进行了重新筛选。特别是，该文首次发现了实体经济的“虚拟化”问题对地下经济模型的估计结果会产生重要影响。他认为“M0相对比例的下降反映了这样一个事实：即货币的虚拟化程度越来越高，现金作为传统流通手段的地位正在被电子货币、电子支付等逐渐挤占。”迄今为止，我国已经有数十位学者先后使用现金比率模型及其多种变形对我国的地下经济规模进行了测度，货币模型成为国内学者最常使用的地下经济估测模型①因列表过长，此处仅部分列举了相关学者的研究，具体可参见王永兴（2010）的系列研究。。

在货币模型以外，国外曾经使用过的另外一些估测方法也在我国得到了不同程度的应用和发展。如夏南新（2002）和赵黎（2006）在 Kaufmann和 Kaliberda（1996）提出的电力消费模型基础上构造了“货运量”模型估计方法，具有一定的创新意义。夏南新（2002、2004）、李炳林和刘洪（2006）分别使用灰色系统模型对我国地下经济规模进行了估测。王永兴（2009）则使用了“能源消耗”模型、收支差异模型等多种方法对我国的地下经济规模进行了估算。然而从总体上看，无论是在国际还是国内，这些方法的应用范围都非常有限，仅电力消费模型在“转型国家”曾经得到过比较广泛和持续的应用。纵观国内外目前流行的地下经济估测方法，除传统的货币模型以外，另外一种就是结构方程模型（MIMIC）的方法，我国学者近年来对这一模型的运用也取得了很大进步。徐霭婷和李金昌（2007）最早使用 MIMIC模型对我国 1985—2005年的地下经济规模进行了测度，他们选用直接税总额/GDP、间接税总额/GDP、失业率、政府实际消费/GDP、自我雇佣人数/15岁～64岁人口数和个人可支配总收入/GDP作为“内生指标”变量（Cause），选用人均实际 GDP、现金占 M1比重作为外生指标（Indicator）。这是中国学者应用这一模型估测地下经济规模的首次尝试，具有引领意义，但在“直接税”指标的理解和使用上存在一定争议。此后徐正云（2009）也使用这一模型进行了研究，其模型中选用2004年全国第一次经济普查数据推算的地下经济占GDP比重作为“基准值”，这种处理方式实际上假定普查方法能够准确反映地下经济规模，然而实际上目前尚没有足够的经验研究结果能够支撑这一假定。杨灿明和孙群力（2010）首次使用面板数据对我国“省际”层面的地下经济规模进行了测算，其研究具有一定的开创意义。刘国风和王永（2011）则使用 EMIMIC模型分别从长期关系和短期关系的角度测算了我国地下经济规模，其选用的指标与徐霭婷等（2007）基本相同，但引入了误差修正理论的思想。近年各国学者对地下经济估测模型的研究并未突破货币模型与 MIMIC模型的框架，主要工作还是围绕如何处理这两种模型的缺陷来展开。由于计量经济学技术的发展，我们发现早期使用的货币模型在数据处理上存在天然缺陷，比如未考虑变量的内生性问题，对时间序列数据的平稳性、对是否存在“协整”关系等问题也未进行考虑。一些学者试图用误差修正理论、自回归分布滞后模型等方法处理此类问题，并取得了一定进展。然而，这些改进并未解决传统货币模型隐含的根本性问题。

首先，外在假设条件的合理性问题。传统货币模型建立在三个基本假设基础之上，即假定现金是地下经济活动的唯一交换媒介，存在一个地下经济为零的“基年”（正规部门的现金/存款比率不变），地下经济与正规经济的收入流转速度相同。王永兴（2009）发现基于这些假定进行计算会出现异常值，Kholodilin和 Thiessen（2011）使用38个OECD国家1991—2007年的面板数据的研究也发现地下经济对货币流通速度的假定非常敏感。王永兴（2009）的解决方法是对这些假定条件依次进行修正，最终通过对“现金/存款”比率的动态化模拟初步解决这一问题。然而，该研究对第一个和第三个假设条件的讨论仍然是不充分的，仅就“高于”、“低于”两种情况进行了初步的模拟，尽管获得了理论意义上的启示，却无法提供具体的量化结果。作者没有进行深入讨论的原因具有客观性，受到当前该领域的研究水平限制，我们还无法在诸如“有多大比例的地下经济活动最终基于现金的形式来完成”、“地下经济货币流通速度与正规经济差异大小”等问题上得到更多的指引。回答这些问题的最直接有效的方法可能是依据大规模的微观调查数据，但如前所述，我国在这方面的工作仍处于空白阶段。

其次，隐含假设条件的合理性问题。货币需求模型实际上还隐含了一些可能会对结果产生全局性影响的关键假设。我们在这里讨论的第一个隐含假设是激励人们从事地下经济活动的“唯一”原因是税收，这一假设是一个简化模型的现实选择，可能带来致命问题①Pickhardt（2011）的研究尽管解决了原始现金比率模型的主要问题，但他也同时强调这并不能减少对这一模型的批评声音，特别是关于它的夸张假设、随意性和不能解释地下经济行为的原因等。。事实上，越来越多的实证研究表明在不同的国家或同一国家的不同发展阶段税收发挥的作用可能是各不相同甚至截然相反的，税收结构、税收道德等方面的因素在模型中完全没有反映。更重要的一点是，在少数国家税收甚至不是地下经济形成的最重要原因，这些发现提示我们不能脱离一个国家或地区的特殊背景来使用模型；需要讨论的第二个隐含假定是“基年”之后现金比率的变化是由地下经济的发展引发的。然而，现实中现金比率的变化原因可能是多元的，特别是随着虚拟经济的发展，现金本身地位的下降已经成为一种内生性的趋势。如图 1所示，我国改革开放以来的“现金-存款”比率变化趋势明显呈“倒U型”，即在1990年以前快速上升，此后则不断下降并一直持续至今。这种情况的出现可以有两种解释：一种解释是这表明我国地下经济相对规模也表现为先升后降的规律；另一种解释则是这反映出现金在我国货币体系中的重要性发生了系统性变化。目前研究的难点之一在于无法确认“现金-存款”比率的变化在多大程度上是由于地下经济的变化引起的，二者相关性的强弱对模型解释力会产生至关重要的影响。从模型结构上看，简单地做出二者之间完全相关的假定在20世纪90年代以前不会产生严重的问题，但在电子化交易手段高速发展的今天则有可能产生严重误导。再进一步思考，尽管现金在世界各国的货币体系中的重要性普遍下降，但在我国的情况可能更特殊，即由于“货币超发”问题的存在，现金地位的变化有可能偏离了世界各国平均的“自然”趋势。截至 2016年底，我国的广义货币（M2）供给量已经超过 155万亿元人民币，超过同期 GDP的两倍，而美国当年 M2的发行量也仅相当于 65万亿元人民币，仅相当于其 GDP的三分之二。这一事实表明我国的广义货币供给路径并不符合“通常”的轨迹，由此也使得相关货币模型中的现金-存款比率等指标解释力下降。

图1 中国“现金-存款”比率变动趋势（1978—2016年）

可见，使用货币模型估测中国地下经济的规模目前还存在一些难以回避的问题。特别是，由于目前国内外学术界对这些问题的研究尚不深入，暂时还难以对我们的实证模型提供有力支撑。在这种情况下，为了对中国地下经济规模进行合理估测则需要转换模型构建的思路，适当淡化货币因素的影响。使用实物估测模型能够最彻底地避免货币非常规波动的影响，但其缺陷在于仅能反映与实物存在密切联系（如电力、货运量）类型地下经济的发展。事实上，无论是货币方法还是实物方法都隐含了一个天然缺陷，即假定用单一指标即可“捕捉”到所有地下经济活动的影响。这一假定显然与我们前文讨论的地下经济多样性特征相矛盾，现实中的地下经济与产品市场、货币市场乃至劳动市场都是直接相关的，如果模型未考虑到这些市场之间的关联而仅单独考察其中一个市场就可能产生片面认识。此外，根据王永兴（2009）的研究，尽管电力消费模型在转型国家的应用相对比较成功，但该模型的原始版本并不适合直接在我国经济超高速发展的特殊背景下使用①从实物模型出发研究我国的地下经济规模尽管并不全面，但也是非常有意义的工作。因为这种方法从逻辑上分析非常“自然”，对其原始模型进行改进使之适用于经济周期中的“高涨”阶段是一项有挑战性的工作，可以作为我们今后研究的一个方向。。

“多指标多因素”模型（MIMIC）可以最大限度地避开上述障碍，从而更全面地反映我国地下经济的发展状态。根据我国的具体情况，使用这一模型可以有两种选择：第一种选择是沿着王永兴（2009）的路径从全国整体层面入手使用这一模型，但由于我国在很多指标上缺乏连续的月度数据，而年度数据样本容量较小，需要仔细检验其统计特征的适用性；第二种选择是沿着杨灿明（2010）的路径采用面板数据（省际数据）进行估计，这样做的好处是可以扩大样本容量，同时还可以得到省际水平的地下经济估测结果。然而，沿着这一路径出发会遇到两个难以回避的问题。首先，MIMIC模型的计算需要以“第三方”模型计算出的某年地下经济规模作为基础，但实际上在省级水平上我国尚不存在比较可靠的地下经济规模估测结果①第三方估测模型首选是货币需求模型，但省际层面的数据无法使用这一模型。。相对而言，全国水平上的地下经济规模研究已经比较充分，对“基准年份”第三方估测结果的选择空间就比较充分。其次，受到统计层次以及数据可得性的限制，使用省际水平的数据必然要舍弃一些重要的指标变量，如货币指标等，而全国水平的数据此类问题相对较少。基于以上原因，我们仍选择从全国整体的层面进行研究，但在指标选择等方面需要根据理论的进展进行调整，使之与中国经济转型时期的特殊初始条件和制度背景更加契合。

Zellner（1970）最早使用结构方程模型进行经济学研究，早期此类模型多围绕“顾客满意度”等问题构建，直到20世纪80年代才有学者把这种模型引入地下经济研究领域。此后，Aigner、Schneider和Ghosh（1986）、Giles（1999）、Loayza（1997）、Giles和Tedds（2002）、Dell′Anno 和 Schneider（2003）、Bajada 和 Schneider（2005）、Dell′Anno（2007）、Macias（2008）、Buehn 和 Schneider（2008）以及 Schneider（2010、2012）等推动了结构方程模型在地下经济中的应用，特别是 Bajada和 Schneider（2005）使用面板数据结构方程模型对世界 100多个国家和地区的地下经济规模进行了估测，这一工作可视作是该模型发展的一个高潮。从国内外研究文献的发展情况来看，结构方程模型代表了地下经济规模估测技术的最新进展，目前已经取得了与传统货币模型基本相同的地位。

在地下经济研究中实际使用的是结构方程模型中的一种特殊类型，一般称为“多指标多因素”模型或 MIMIC模型（Multiple Indicator Multiple Cause）。这种方法虽然出现时间较早，但我国引入较晚，2000年以后才出现使用结构方程模型的应用研究成果（侯杰泰、温忠麟、成子娟，2004）。结构方程模型独特的优势在于可以用来研究一些无法直接观测的变量，具有这种特性的变量被定义为“潜变量”，而 MIMIC模型就是模型中只有一个“潜变量”的“零B”模型。使用MIMIC模型估测地下经济规模的基本逻辑就是把地下经济的规模（或对应变化率）视作是一种“潜变量”，虽然地下经济规模无法直接观测（参见定义），但可以通过建立与“指标变量”、“原因变量”的联系间接反映其变化。根据可观察的样本数据拟合模型中的参数，在满足对应“识别”条件的前提下很容易借助相关软件估算出来参数，进而确定地下经济的相对规模。这种方法也需要引入第三方模型的估计值作为基准值，基准值的选择对最终估算结果影响较大，必须谨慎选择①例如，假如使用货币方程模型作为“第三方”结果，那么货币流通速度等关键假设就会对 MIMIC模型产生潜在影响。。此外，基准方法的选择也非常重要，正如 Dell′Anno（2007）等所强调的：“在当前的结构方程模型研究阶段，具体应该使用哪种基准计算方法仍然是不确定的。”可见，使用结构方程模型估测地下经济规模的方法需要结合不同国家的实际情况进一步探索和完善。综合比较以上各类模型的特点，本文将采用“多指标多因素”模型对我国地下经济规模进行实证研究。

三、模型设计

“多指标多因素”模型（MIMIC）实际上属于结构方程模型（Structural Equation Modeling，SEM）的一种，SEM 至少在三个方面有别于传统的计量经济模型：第一，可以同时处理多个被解释变量；第二是可以对潜变量（latent variable）进行测度；第三，既可以处理变量间的直接影响，也可处理间接影响。就地下经济规模估测的目的而言，MIMIC模型可以直接把地下经济视作“潜变量”或不可观测变量，然后利用可观测变量的样本协方差矩阵来分析二者之间的关系，由此可以利用一套系统化的方法对其参数进行估计。更重要的是，MIMIC模型可以同时考察多个（引致地下经济发展的）“原因”变量和多个“指标”变量，从而突破了传统方法的局限。一般化的结构方程模型由测量方程（方程1和方程2）与结构方程（方程3）两部分构成：

公式（1）—公式（3）中各种符号的含义如表1所示。

表1 结构方程模型中各种符号代表的意义

MIMIC模型是结构方程模型的一种特殊形式，即外生变量都是可测变量，但存在一个或多个内生潜变量。我们研究的地下经济模型就是仅包含一个内生潜变量的MIMIC模型，所以该模型的一般形式可以作如下表示：

其中，公式（4）度量了潜变量η与原因变量Xq之间的关系，公式（5）则把潜变量η与内生指标变量Yp连接起来。两个方程的误差项均需要满足零均值假定、联合正态分布和独立性等条件，其简化形式如下：

其中 p是外生指标变量（或测量变量）的数量，q是内生指标变量的数量。判别规则是：当小于号成立时，模型为过度识别；当等号成立时，模型为充分识别。当模型中不存在结构关系时（即没有内生变量影响其他内生变量），B矩阵为 0，模型符合Bollen（1989）所说的“零 B”规则（Null B Rule），此时整体模型自动可识别。此外，测量方程也必须满足识别性原则，这主要涉及量尺的设定问题（scaling），为方便处理，对于内生潜变量一般指定其所影响的一个测量变量的因子载荷为 1（或－1）。图 2展示了MIMIC模型的总体结构。

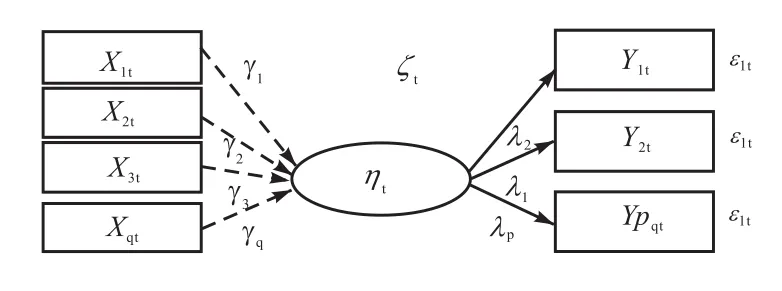
图2 MIMIC模型的一般结构图示

根据MIMIC模型的基本原理，我们把地下经济视作内生潜变量，模型估测第一个阶段的首要问题是选择理论上可接受的内生指标变量和外生指标（原因）变量进入模型，再根据一系列评价指标进行筛选。

国内外学者已经尝试了数十种内生指标变量和外生原因变量，由于理论认知上的分歧，也由于各国的国情存在巨大差异，不同学者在指标选择的数量、类型等方面各不相同。为了得到有说服力的模型结果，选择有一定理论或应用基础的并具有逻辑说服力的指标变量尤为重要，为此必须首先对每个进入模型的变量进行充分讨论，在此基础上再根据模型的拟合情况进行筛选以确定最终选用的外生和内生变量①这里的“内生”变量指的是模型中会受到其他变量影响的变量，在路径图中表示为被单箭头所指的变量。“外生”变量则是指对其他变量有影响但不受其他变量影响的变量，在路径图中表示为指向其他变量，但不被其他变量以单箭头所指的变量。。

（一）外生原因变量

根据国内外现有文献，MIMIC模型中对外生原因变量的选择相当宽泛，这个指标集已经包含了 20多个元素，其中使用频率较高的是税收总量占 GDP比重、失业率等指标。我们总结 MIMIC模型指标选取应该遵循以下步骤或原则：首先，必须考察该指标与地下经济发展之间是否存在逻辑上的因果联系，这一要求比较容易得到满足。其次，考察该指标在目标样本国家是否能够获取有效的对应数据，这一步骤常常会遇到困难。实际建模过程中常常只能通过寻找近似的替代性指标来解决，甚至很多时候不得不直接放弃一些理论上非常符合要求的指标。再次，应结合目标国家的具体国情进行指标筛选。以税收相关指标为例，由于各国的税制结构、税收传统、税收道德等情况迥异，不同类型的税种与地下经济的关联程度也必然存在差异。

具体来看，国内外学者经常使用的外生原因变量包括：劳动参与率、名义汇率、劳动力实际人均可支配收入（或其占GDP比重）、营业税占GDP比重、间接税占GDP比重、直接税占GDP比重、福利和转移支付支出占可支配收入比重、失业率、税收总量占GDP比重、政府消费占GDP比重、政府实际消费（或其对数）、通货膨胀率、犯罪率、自我雇佣者数量占劳动力总数比重、电力消费数量、公务人员占劳动力总数比重、劳动市场弹性、政府应对逃税问题的对应支出等。这些指标均满足第一个筛选原则，但实际数据整理过程中发现存在大量问题，主要问题包括：很多指标在我国缺少对应口径的数据；部分指标尽管能找到对应数据，但由于统计口径经过多次调整合并，可比性存在一定问题；还有一些指标缺乏改革开放初、中期的数据②例如，我国1980年才颁布《中华人民共和国个人所得税法》，1985年才开始征收企业所得税。实际演进过程更为复杂：1986年又开征了“城乡个体工商户所得税”，1987年开征“个人收入调节税”，直到1994年才合并为现行的个人所得税口径。。结合我国自身的数据特点，初步选择如下指标作为“外生原因变量”。

1. 名义汇率（NE）。汇率的波动对资本流动和对外贸易造成影响，这会对走私等形式的地下经济造成影响（Giles和Tedds，2002）。改革开放以后，虽然我国汇率并未完全放开，但汇率市场化的进程一直在推进，本文使用人民币兑美元汇率作为代理变量。

2. 税收总量（TTAX）占 GDP比重。税收是地下经济形成的重要原因，这是目前该领域学者取得的基本共识，也是诸多模型的研究起点（Tanzi，1983；Feige，1986；Buehn和 Schneider，2012；等）。现有文献对各类税种均有所侧重，理想的处理方式是把各主要税种均分别纳入模型，再根据判别指标进行筛选，但由于我国改革开放后各税种经历较多调整，单个税种的数据难以满足要求，只能以总税收进行替代。

3. 社会保障支出占 GDP比重（SS）。社会保障水平越高，人们出于生存目的而参与地下经济的动机越弱（Bajada 和 Schneider，2005；Dell′Anno，2007），但高水平社会保障如果建立在过高的税收基础上则可能间接推动地下经济的增长。由于我国的社会保障体系建立较晚，这方面的样本数量不足，因此用医疗卫生机构个数作为代理变量。

4. 政府规制（GC）。政府规制的程度往往与地下经济密切相关，规制程度过高或过低都有可能促进地下经济的发展（Dell′Anno，2003、2007；Macias，2008）。具体可采用公务人员占劳动力总数和政府消费占 GDP比重来代表规制程度，一些文献也用政府实际消费（或对数）来替代，本文采用政府消费比重作为代理变量。

5. 城镇登记失业率（UER）。较高的失业率往往意味着实体经济出现某些问题，部分失业者会被迫从事与地下经济有关的工作，多数文献都引入失业率作为外生原因变量（Giles和 Tedds，2002等）。由于我国“调查失业率”的数据并未公开发布，本文只能用准确度和代表性较差的城镇登记失业率进行替代。

6. 通货膨胀率（IF）。较高的通胀水平预示宏观经济不稳定，其影响可能是双向的。严重通货膨胀引致的正规经济崩溃会刺激地下经济的发展，但通货膨胀引起的收入分配效应也会同时缩小与现金交易相关的地下经济规模（Wang等，2006；Macias，2008）。本文采用CPI数据作为代理。

7. 自我雇佣比率（SER）。部分地下经济的从业者往往具有自我雇佣的特征，自我雇佣的比率越高，往往意味着地下经济规模越大（Giles和 Tedds，2002；Schneider和Dell′Anno，2003）。由于数据限制，我们采用城镇个体就业人数作为代理变量。

8. 电力消费总量（EC）。电力消费是反映实体经济运行情况的重要变量，某些地下经济虽然逃避了统计部门的监督，但其与电力消耗相关的部分无法隐藏，较高的电力消费水平往往也反映出地下经济规模的增加（Kaufmann和 Kaliberda，1996；Rosser，2000；王永兴，2010）。

9. 犯罪率（CR）。政府致力于降低犯罪率的努力会使从事地下经济活动的收益减少，因此二者可能存在正向联系，Eilat和 Zinnes（2000）的实证研究也发现犯罪率提高会导致地下经济更快增长。由于我国缺少犯罪率的直接数据，我们采用人民法院审理一审案件收案数作为代理变量。

（二）内生指标变量

内生指标变量的选择标准与外生原因变量基本相同，但选择空间相对较小。这里需要强调的是，正如 Buehn和 Schneider（2012）所认识到的，内生指标变量与外生原因变量并没有绝对的界限，某些内生指标变量在特定情况下也可以作为外生原因变量。从国内外文献的发展情况来看，常用的指标主要包括：实际 GDP（或对数）、公众持有的现金量（或对数）、人均实际现金持有量对数、现金比率、人均实际 GDP（或对数）、现金占M1比重、实际GDP与适龄劳动力总量比率、劳动力参与率、M1与M3比率、实际 GDP指数、流通中实际现金持有量等等。这些指标可以归纳成三大类，即反映产品市场发展情况的指标、货币市场指标和劳动市场指标。

1. 实际 GDP。实际 GDP是用来指示产品市场发展情况的常用指标，选用此类指标的逻辑是地下经济与官方正式经济之间存在密切联系。需要指出的是，地下经济对正规经济的影响方向尚存争议。Bajada（2005）等认为，地下经济的增长可能意味着要素从正规经济中流出，从而降低正规经济的增长潜能（Bajada，2005）。Tedds（1998）、Giles（1999）以及Giles 和Tedds（2002）则发现二者之间存在某种正向联系。

2. 现金/存款比率（CD）。现金/存款比率是代表货币市场变化的重要指标，选用此类指标的逻辑是地下经济的发展往往会产生额外的货币需求，特别是某些地下经济交易是以现金为媒介完成的（Wang等，2006）。不过随着虚拟经济的发展，电子化交易日益替代现金成为交易的主要媒介，这会对传统的地下经济交易手段产生深远影响（王永兴，2010）。鉴于此，我们也引入“现金/M1”比率（CM）和“M1/M2”比率（M12）作为竞争模型。

3. 劳动力参与率（LR）。选用此类指标的逻辑是地下经济的发展意味着参与地下经济活动的劳动力（或劳动时间）增加，这会导致参与正规经济的劳动力（或劳动时间）相应减少（Dell′Anno，2007）。不过需要注意的是，如果个人只是在下班后或周末从事地下经济活动，那么劳动参与率指标就无法全面反映地下经济的发展情况。

四、数据与描述性统计

本文的数据主要来自国内外公开的数据库和统计年鉴，表 2是关键变量的描述性统计特征，具体的数据来源及口径说明如下。

表2 外生原因变量和内生指标变量的描述性统计

1. 名义汇率的数据来源于美国联邦储备银行。

2. 税收数据来源于《中国税务年鉴》。

3. 公务人员来自《中国劳动统计年鉴》国有经济单位中的国家机关、政党机关和社会团体。

4. 公安机关刑事案件立案数的数据来源于《中国法律年鉴》。

5. M1与M2、社会保障支出的数据来源于中经网统计数据库。

6. 中国15岁以上的人口数来自于《中国人口统计年鉴》。

7. 其他未作说明的数据都来自国家统计局网站以及历年《中国统计年鉴》和世界银行数据库。

通过表 2可以对变量的基本统计特征形成初步的认识。由于改革开放以来，我国经济出现了超高速的增长，因此部分经济指标变异较大，在后续进入软件进行估算时，数据会进一步进行差分处理。

五、实证结果

（一）基准值的设定

由于 MIMIC的测算需要引入一个第三方模型某年的估算结果，一些学者选择样本起始年份的第三方值作为基准，但考虑到不同学者对同一年份的估算结果可能会存在差异，另外一些学者则以“该年度可引用测算结果”多少作为选择标准，再对该年份结果取均值。为了保证第三方估计结果更具有权威性和可信性，我们对现有文献的模型估计结果进行了分析，计算每一年份估算结果的标准差，最终选择标准差最小的年份的均值作为基准。具体筛选过程见表 3，根据上述判别标准，可选择 1991年的估算值均值进入模型，通过计算得知该年地下经济规模相当于官方GDP的14%。

表3 第三方估算值筛选表

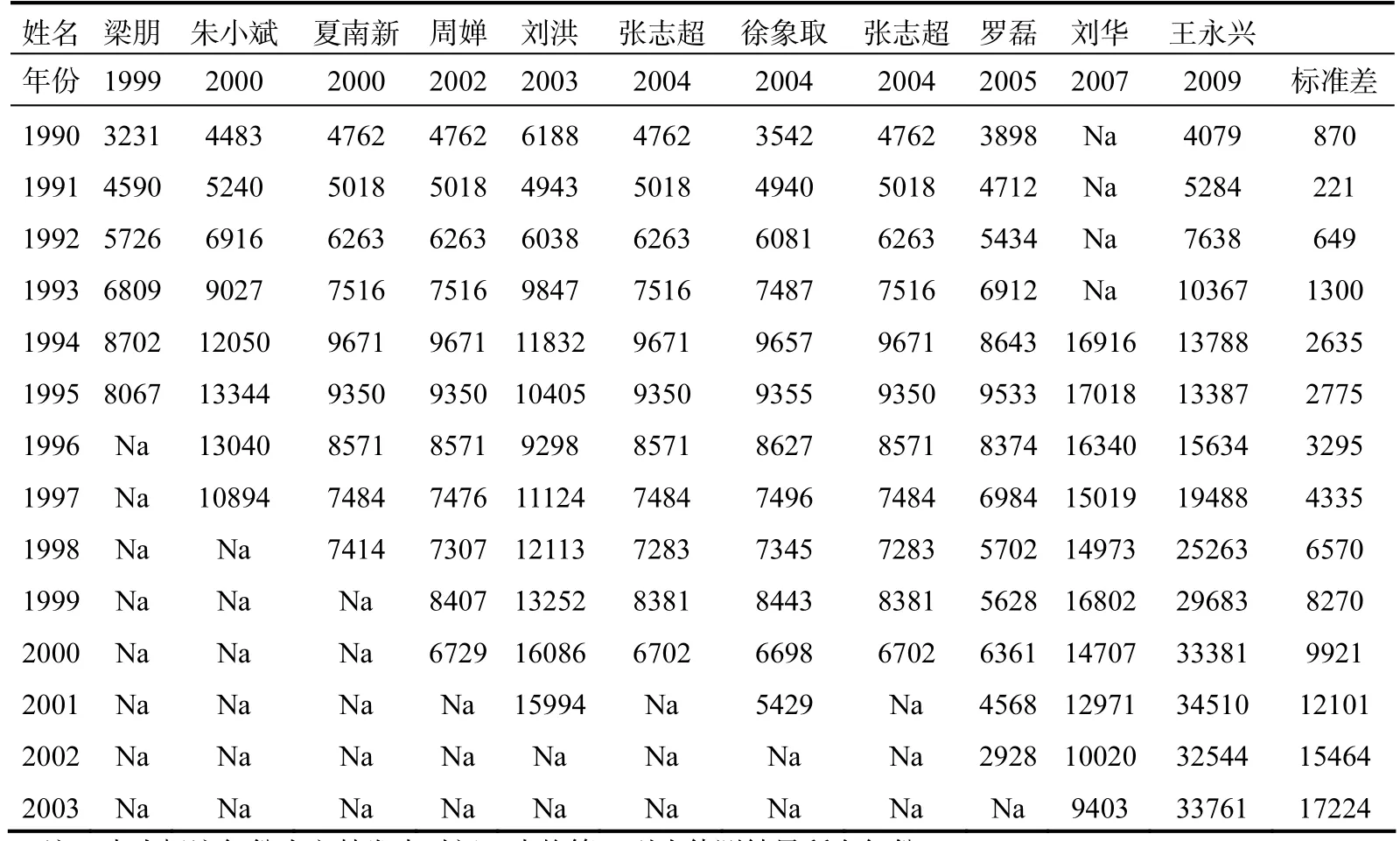
续表3

（二）模型的拟合结果及评价

我们最终选择“9-1-3”形式的MIMIC模型作为基础模型进行估算，再根据拟合指标进行模型“竞争”，逐步淘汰不合意的模型，最后确立最合适的模型形式。表4展示了模型估测的主要结果，目前处理此类模型的软件有AMOS、LISREL、EQS和Mplus等多种，本文选用AMOS（Analysis of Moment Structures）软件对模型进行拟合估算，其中模型1为基准模型，模型2至模型8为竞争模型。由于内生指标变量中的货币变量存在多个代理变量，我们逐一进行了迭代拟合（基于最大似然法），然后根据各变量的显著性水平以及 RMSEA、GFI以及卡方等常用的模型修正指标进行筛选。在基准模型（1）中，误差均方根、比较拟合指数等指标低于 0.9，表明拟合情况未达到理想状态，在替换内生指标变量后，结果未出现明显变化。在此基础上，依次对外生原因变量进行调整，观察模型评价指标的变化，最终确定使用模型8进行测算①各种指标组合包含数十种情况，受篇幅所限，本文仅列出部分前期、中期和最终模型估算结果。。

由于MIMIC模型还处于发展中阶段，目前尚不清楚哪种校准方法是最优的。本文采用Schneider（2006）所提出的校准方法，具体过程如方程（8）所示：

其中第一项为模型估算指数序列，第二项为第三方模型某特定基年估算值，第三项为模型估算的特定基年估算结果，最后一项可以把一个地下经济相对基年 GDP的指标序列转化为地下经济与当年 GDP的比值。通过以上程序，我们对 1979—2016年中国地下经济相对于同年GDP的规模（比例）进行了测算，得到的结果如图3所示。

表4 MIMIC模型拟合结果筛选

从估算结果上看，改革开放以来，我国地下经济的规模波动较大。其中 1990年相对规模最小，仅相当于当年GDP的3.53%，而2003年规模最大，达到了18.81%。从总体上看，20世纪80年代中期左右和90年代早期以及2003—2009年这三个阶段我国地下经济活动比较活跃，而在2010年后总体呈现“趋势性”下降特征，特别是最近几年地下经济发展变缓，与上一个周期相比，下降到了5%以下的水平（相对同期GDP）。通过对比中国历年GDP增速可以发现，我国的GDP相对规模与中国经济的发展周期高度相关，其背后的联动机制主要通过电力消费、非正规劳动力市场等中介因素发生作用。由此可见，考虑到地下经济的影响，中国的真实经济规模一直存在系统性的低估。随着近年统计制度的逐步完善，低估的程度呈现降低趋势，即官方的统计核算反映真实经济活动的能力日益增强。但必须正视的一点是，虽然近年地下经济的“相对”规模并不突出，但2007—2016年的绝对量始终处于2万亿到7万亿人民币的区间，可见地下经济客观上已经成为我国经济社会中潜藏的一股不可忽视的重要力量①例如，考虑到地下经济规模部分，2015年和2016年的实际经济规模将分别调整为71.9万亿元人民币和76.8万亿元人民币。。

图3 中国地下经济的相对规模（1979—2016年）

六、研究局限及可能的发展方向

地下经济对中国经济、社会等方面的宏观影响已经引起我国学者的关注（王永兴，2014），深入研究地下经济具有明显的政策意义。然而，目前地下经济仍然是一个远未成熟的研究领域，我们对中国地下经济规模的研究不可避免地存在各种不足。一方面，研究方法本身尚存在一些暂时无法弥补的天然缺陷；另一方面，研究也面临着数据可得性、样本容量等方面的制约。

（一）样本容量问题

结构方程模型的稳定性通常会随着样本容量的增加而增强，但对具体需要多少样本尚未形成一致的认识。Anderson和 Gerbing（1988）认为最低需要 100个～150个样本，多多益善。Hu和 Bentler（1992）等学者甚至提出对某些研究来说，即使 5000个样本也不一定能够得到满意结果。在实际运用这一模型的过程中，样本容量往往受到客观条件的限制。对于心理学等领域的研究而言，即使相对小范围的微观调研抽样数据也比较容易满足样本数量的要求，但很多基于宏观数据的研究则较难达到理想中的状态。一般规律是年度水平上可利用的变量最为丰富，半年度水平的数据次之，季度和月度数据最少。这种情况在统计制度相对不完备的发展中国家更为普遍，很多重要宏观经济变量缺少对应的季度、月度统计，或仅从近年才开始统计，这样在样本容量上无法满足建模的需要。从目前地下经济的研究情况来看，多数学者选择使用年度水平数据进行研究，如 Giles 和 Tedds（2002）、Wang 等（2006）、徐蔼婷和李金昌（2007）、Macias（2008）等的研究均是如此，他们使用数据的样本容量多处于20个～40个的区间。从国内外现有文献的发展情况来看，只有极少数使用季度数据的研究以及使用跨国面板数据的研究获得了较高的样本容量，因此在国内外的地下经济规模估测研究中选择有限的“年度”数据仍然是现有条件下的一个现实且可行的选择。

尽管存在诸多困难，但可以预期的是这一问题有希望通过两种途径得到解决。第一个途径是，在将来关于我国省际水平的地下经济规模估测的研究能够形成系列性的和比较成熟的成果后，就可以为基于面板数据的MIMIC方法建立基础；第二个途径则有赖于统计制度的完善发展，随着我国未来半年度、季度以及月度统计数据的丰富，样本容量问题也可以通过使用季度月度等频率较高的数据得到部分解决。

（二）微观数据缺乏问题

本文所使用的计量经济模型基于宏观数据，这不可避免地会产生一些缺陷。尽管我们已经对地下经济的微观基础进行了比较广泛的探讨，但还只是限于理论上的推演，尚缺乏扎实的微观数据对其结论形成有效支撑。直接调查法在地下经济研究中具有不可替代的意义，我们预计至少应采取分层随机抽样的方法在全国范围内以户或个人为单位抽取 5000个左右的样本。在理想的情况下，直接调查法甚至可以直接推算得到地区级的地下经济规模，这又为基于省际数据的MIMIC模型提供了基础。

在下一步的研究中，我们需要获取更多的微观调研数据进行补充，这样才能对某些理论问题提供经验上的检验和支撑。譬如，只有通过大量微观调研或行为实验才能更精确地描述地下经济参与人的行为动机，是纯经济利益考虑还是包含了其它的复杂因素，是纯利己主义驱动还是包含了某些利他主义因素等。同时，这也能够为地下经济治理政策提供最直接的决策依据。

（三）全国经济普查带来的思考

经济普查是各国统计实践中的普遍做法（如美国早在 19世纪初即开展了普查工作），这对提高统计数据的质量和指导国民经济实践非常重要。由于历史条件所限，我国在 1992年首先对第三产业的发展情况展开普查。一直到 2004年我国才开始组织进行全国性的经济普查。不难发现，根据普查结果调整后的我国 GDP规模与调整前相比存在明显差别，我国 2004年第一次经济普查得到的经济总量数据要比常规公布的 GDP多 23002亿元。徐蔼婷（2007）等学者认为这部分差额可由地下经济活动来解释，王永兴（2009）也曾使用普查数据及历史数据修订值的对比来计算地下经济规模。尽管这种方法无法全面地反映地下经济的真实水平，但对厘清地下经济的产业分布情况有重要作用。由于普查年度的 GDP差异 90%以上来自第三产业，我们有理由推断我国的地下经济在第三产业中的发展较快。我国第四次全国经济普查标准时点是2018年12月31日，这次普查与以往相比手段更为规范，程序和工具也更现代化。可以预计的是，随着我国经济普查工作的深化，我国的统计数据质量将大为提高，由此可为中国地下经济问题的研究提供更好的参考。

最后需要强调的是，地下经济估测方法是多元的，尽管MIMIC模型具有不可替代的优势，但也同样存在很多局限。从学术研究的视角来看，许多学者（Dell′Anno，2007；Buehn和Schneider，2012）都曾多次强调在使用此模型估测结构的同时必须注意其局限性。虽然使用该方法得到的中国地下经济规模估测结果具有重要的参考意义，但不宜把结果绝对化。