数形相依,绽放思维之花
2019-01-16林吟艳
林吟艳
借助直观形象模型理解抽象的数学概念以及抽象的数量关系是小学生学习数学的重要方法。教学活动虽然有图形、有算式,但活动中不关注这些图形的形状与度量特征,而是关注图形的个数,并没有渗透数学意义上的“数形结合”思想。这一现象引起了笔者思考,“数与代数”领域中哪些知识点可以渗透“数形结合”思想?
一、借助数轴,理解抽象的概念
数学知识本身是抽象的,建立直观是非常必要的,而数形结合是建立数学直观的有力工具。小学生的逻辑思维能力比较弱,他们对抽象概念的理解基本上要借助感性的直观材料,借助数形结合图形直观的特点,为抽象概念的学习提供了较好的方法。数轴实现了数与形的联系,将数与直线上的点建立了对应关系,揭示了数与形的内在关系,从而使抽象的“数”有“形”可依。
【片段】求一个数的近似数。
师:0.984保留一位小数的近似数,为什么是1.0,而不是1呢?末尾的0到底该不该去掉呢?
操作要求:请同学们借助这条数轴“找一找、圈一圈、画一画、议一议”,分别找到近似数是1和1.0的数。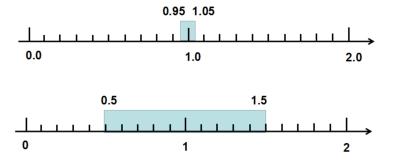
师:从刚才同学们画的范围可以看到,近似数是1的范围是0.5~1.5(不包含1.5),近似数是1.0的范围是0.95~1.05(不包含1.05),也就是说,近似数为1.0的精确度要更高点。保留的小数位数越多,近似数的精确度越高,正因为这样,在表示小数的近似数时,末尾的0是不能省略的。尽管大小相同,但精确度会受影响。
借助数轴对比,学生直观感受到保留的位数越多,近似数的精确度越高。可以追问学生近似数1.00的范围、近似数1.000的范围,拓展思维,体验极限的思想。数形结合使“数”与“形”统一起来,丰富了学生对数的形象感知,发展了学生的数感。
二、借助线段图,理解抽象的数量关系
解决问题作为一种贯穿整体的教学方式,每时每刻都在进行。具体问题的题意理解、数量关系分析、问题解决策略的形成都离不开直观手段的运用。归一、归总问题是建立两步问题数量关系和形成学习方法的关键,是培养画图意识和画图能力的关键。以下是学生归总问题画的线段图:
通過线段图比较,明确画图时反映信息问题要准确全面,通过寻找共性特点,帮助学生发现中间问题或关键因素,即学生要解读出总量不变这一关键问题,并在线段图上反映为长度相等,又要用不等长的线段区分6元与9元价钱,在“等长”和“不等长”的图示表达中经常会顾此失彼。此时,引导学生围绕“整条线段表示什么”“同样长是反映哪条信息,同样长想表达什么信息”等问题展开讨论,梳理各信息之间的内在联系和画图步骤,帮助学生全面、有序地表达题意。线段图对解题思路分析、整理数量关系、数学模型建构都有明显的直观效果。
三、借助“面积模型”理解分数及运算算理
学生只有理解了算式的意义,才能正确地运用算式解决问题,对算式意义的理解实际上是对运算意义的理解。运算的含义对学生来说是抽象的,学生理解这些抽象的概念会有一定的困难,一定要处理好直观与抽象的关系,加强直观教学,突出从概念的本质上理解运算的意义。
【片段】连除简便计算。
师:像600÷2÷3=600÷(2×3),400÷5÷2=400÷(5×2),900÷3÷10=900÷(3×10)这样的算式,为什么就相等了呢?你是怎么判断的?
生:左右两边算式的计算结果是一样的,所以相等。
师:是不是只要有这样特点的算式都是相等的呢?100÷4÷7和100÷(4×7)这两个算式相等吗?
学生有的沉默,有的摇头,有的点头。
生:都除不尽怎么判断?
(多媒体出现一个长方形图)
师:如果把这个长方形看成100,100÷4÷7怎么表示?100÷(4×7)又怎么表示?
学生操作。
生:把100平均分成4份,再平均分成7份,就是把100平均分成28份。100÷(4×7)也表示把100平均分成28份。
外在的形式上,a÷b÷c和a÷(b×c)存在明显的不同,当我们把两个算式的意义归结到除法平均分的意义上,结合“面积模型”直观演示,清晰理解“连除性质”的本质。在学习过程中,学生沟通了知识间的联系,建构起了完整的“知识链”。
四、借助“直角坐标系”,初步感知函数思想
学生在学习正、反比例关系时,把两个量在直角坐标系中表示出来,借助于形象的图像,直观呈现两个变量之间的相依关系,深入理解抽象的函数关系。正比例的概念比较抽象,如何让学生正确建构出正比例的模型,关键是带领学生找到正比例最核心的本质,即比值一定。应用数形结合思想可以把抽象的数量关系与形象的直角坐标图联系起来,在“数”与“形”互译中理解正比例的本质,初步感知函数思想。
数形结合思想反映了客观事物深层次的内在联系和矛盾统一。我们要重视数形结合思想在小学数学教学中的运用,让学生在学习中不断积累经验,形成方法和策略,思维获得有效的发展。
