三维随机裂隙介质建模与GPR响应计算

林景宜， 曾昭发， 李 静， 张 领， 槐 楠， 胡志鹏

(1.吉林大学 国土资源部应用地球物理重点实验室，长春 130026；2.吉林大学 地球探测科学与技术学院，长春 130026)

0 引言

土壤和岩石颗粒具有明显的塑性、胀缩性、吸湿性和黏结性，是影响收缩特征的重要因素，岩土的收缩能力与土壤黏粒含量呈显著正相关[1]，在遇水和失水后，会在上述性质差异较大的区域，产生有自相似性的裂隙分布，裂隙具有明显的分维特征，且裂隙率、含水量、渗透系数和变形量之间具有一定的关系[2]；岩土中的裂隙带是岩土中的软弱结构和水的优先流动途径[3]；坡体上裂隙的存在能够导致优先流的发生，使地表水很快到达土壤深层，增大了入渗面积，提高了入渗速度[4]，同时，裂隙受雨水渗透力及渗透侵蚀的作用，不断地延伸、扩大，最终形成滑坡[5]。可见对岩土介质中的裂隙带进行探测，是灾害预警和灾害评价重要的基础。

构成岩土的颗粒和孔隙大小不同，形状各异，并且可能以各种方式连接，结构形状十分复杂，通过常规的欧式几何很难模拟岩土内部的结构。但是岩土结构状况的一些参量，比如粒径分布、裂隙发育程度、联通状况都表现出分形特征[6]，所以近年来，不少研究采用分形理论模拟岩土结构，Perfect等[7]、Perrier等[8]运用QSF分形理论对含聚合物颗粒的碎裂土壤结构进行了定量化模拟；Kravchenko等[9]、Medina等[10]计算出了土壤粒分形模型来模拟土壤结构和不同尺度下质量构成；Shepherd[11]用Koch曲线模拟孔隙通道连通状况问题；Jiang等[12]建立基于混合型自相关函数的多尺度随机介质模型来模拟介质的非均一性。然而，上述研究偏重于对岩土整体结构的建模，未能模拟出岩土中软弱带的局部特征。

岩土介质建模后，对模型进行数值模拟的方法众多，其中探地雷达是对浅层介质探测的重要方法。探地雷达(GPR)数据的分析和解释基于地下介质的电性参数，主要包括介电常数和电导率，应用在介质界面和目标形状的探测方面[13]，在裂隙带探测中也能发挥重要作用。Godio等[14]用探地雷达和其他方法综合探测了含水层的裂隙带和渗透层的几何形态；邓国文等[15]在隧道超前预测中用探地雷达对断层破碎带和裂隙带进行了探测和解释。在GPR数值模拟方面，Li等[16]采用CFS-RIPML边界导出高阶FDTD方法，应用到了GPR数值模拟中，有效降低了数值色散引起的误差，提高了结果的准确性。在结果处理和解释过程中，时频分析方法起到了重要作用，Stockwell等[17]在以Morlet小波为基本小波的基础上提出了可逆的S变换(ST)时频分析方法，S变换采用高斯窗函数，继承了短时傅立叶变换(STFT)和小波变换(WT)的优点，可以有效压制噪声，获得更高分辨率的响应结果；邓攻等[18]使用S变换对深反射地震弱信号进行了分解，提取出了被噪声湮灭的低频细节特征，提高了剖面的分辨率和同相轴的连续性。

笔者在前人研究的基础上，使用三维Koch分形方法和Bruggeman等效介质理论，来模拟真实裂隙带分布，并使用随机等效介质理论建立岩土背景。建立一个三层背景下的裂隙带模型，根据不同含水率计算裂隙的等效介电常数。对模型进行GPR数值模拟，定性研究其波场特征，再对响应进行S变换得到时频特征，定量拟合含水率与响应的关系，最后进行裂隙带深度的误差分析。

1 建模方法

本模型的构建过程主要包括三维Koch曲线构造、裂隙带形态控制、裂隙带位置控制、裂隙成分等效、岩土背景随机化几个步骤。

1.1 三维Koch曲线构造

Koch曲线由瑞典数学家科赫(Koch)于1904年提出，是一种具有典型自相似性的折线，应用三维Koch曲线进行分形建模，可以更好地模拟出裂隙结构的自相似性和联通状况。

图1 满足广义能量极小值原理的三维Koch曲线Fig.1 Three-dimensional Koch curve of the principle of generalized energy minimal value

三维Koch曲线如图1所示，取一条线段P1P5，将其三等分，得到点P2、P4，设P1(xp1,yp1,zp1)、P5(xp5,yp5,zp5)，则由定比分点公式(1)可得P2(xp2,yp2,zp2)、P4(xp4,yp4,zp4)。

(1)

在三维空间中，ΔP2P3P4可以围绕轴P2P4任意旋转，所以点P3(xp3,yp3,zp3)不唯一。在自然界中非线性系统属于强迫耗散动力系统，由广义能量极小值原理和热力学第一、第二定律可知，这种系统在经过足够长的时间后，总是趋向一种不可逆过程最弱、系统广义能量最小的有序状态[19]。裂隙结构属于不规则的非线性复杂系统，也遵循广义的能量最小值原理。

设三维Koch曲线整体为一刚体系统，则其弹性势能为“0”，系统总能量等于重力势能，在系统质量一定时，重力势能与系统重心位置有关，重心位置越低，则重力势能越小，系统总能量也越小[19]。如图1所示，当点P3(xp3,yp3,zp3)在Z方向上最小时，重心位置最低，此时ΔP2P3P4所在平面垂直于平面XOY，过点做一垂线L，由几何关系知，L平行于平面XOY。以L为轴线，将线段P2P4顺时针旋转60，旋转后点P4即为点P3所在位置。

(2)

(3)

M=+cosθ·(I-)+sinθ·A*

(4)

P′=P·MT

(5)

式(2)～式(5)中:A=[ax,ay,az]为单位长旋转轴;θ为旋转角;I为三阶单位矩阵;P为待旋转点的坐标;P′为旋转后坐标。

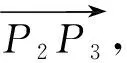
(6)

可求得旋转后的坐标点P3，此时整个系统的总能量最小。将P1到P5的位置都求出后，每两个相邻的点之间再进行相同计算过程，重复几层以后，可递归出一条满足广义能量最小值定理的Koch曲线。

1.2 裂隙带形态控制

在遇水和失水后，会在收缩性质差异较大的区域，产生有众多自相似性的裂隙分布，形成裂隙带。

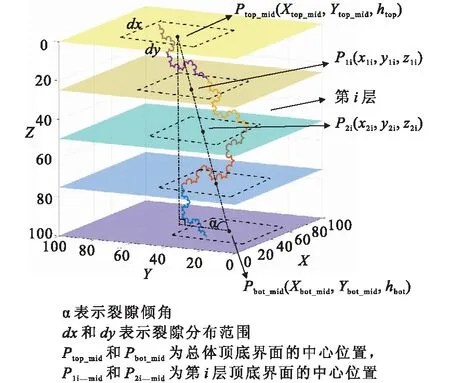
图2 3维Koch分形裂隙的构造过程Fig.2 The construction process of 3D Koch fractal fissure

如图2所示，设裂隙深度上、下限为htop和hbot后，将裂隙沿Z轴分n层，共n+1个界面，每层的底界面即为下一层的顶界面，每段裂隙的底端即为下一段裂隙的顶端。设裂隙带在顶界面的中心点位置为Ptop_mid)(Xtop_mid,Ytop_mid,htop)，底界面中心点位置为Pbot_mid(Xbot_mid,Ybot_mid,hbot)，裂隙带倾角为α，则由几何关系可得：

tanα=

(7)

当Xtop_mid、Ytop_mid和α给定后，可求得一组Xbot_mid,Ybot_mid，确定了Ptop_mid和Pbot_mid的位置(图2)。

(8)

式中:P1i_mid(x1i,y1i,z1i)为第i层裂隙带的顶界面中心点坐标，P2i_mid(x2i,y2i,z2i)为第i层裂隙带底界面中心点坐标。

设裂隙带的长和宽为dx和dy，为了裂隙带在内部体现出每条裂隙位置的随机性，在(xni mid±dx/2,yni mid±dy/2)范围内随机取值，即可得到第i层裂隙的顶端点坐标(x1i,y1i,z1i)和底端点坐标(x2i,y2i,z2i)通过式(7)、式(8)可画出第i层的分形裂隙，将各层连接即为一条裂隙，多次递归上部步骤即可画出一个具有倾角的裂隙带。

1.3 裂隙带位置控制

经过处理后得到固定位置处的裂隙带，还需将裂隙带旋转平移到指定位置。将裂隙带各个转折点位置记为一个矩阵[X,Y,Z]，X、Y、Z均为列向量，

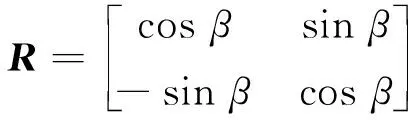
(9)

(10)

式中:β为裂隙带在xoy面上的旋转角度;R为二维旋转矩阵;[Dx,Dy]表示裂隙带在x和y方向上平移;[Xnew,Ynew]为旋转平移变换后的，在z方向上，裂隙带位置没有发生变化;Znew与Z相同。如图3所示，先旋转β改变裂隙带倾斜方向，再平移D改变裂隙带位置。可得裂隙带的旋转和平移后的位置[Xnew,Ynew,Znew]。

图3 裂隙带的旋转平移过程Fig.3 The rotation process of the fissure belt

1.4 应用等效介质方法

经过上几步处理，实际得到的是裂隙带的转折点骨架，还要给裂隙带赋予实际的物理意义。将模型中的每一条裂隙看作是周围众多细小裂隙的等效，不仅能突出需要研究的尺度，还能提高计算效率，应用Bruggeman等效介质理论：

(11)

式中：εeff为Bruggeman等效介电常数；εi为第i类介质的介电常数，fi为第i类介质的体积分数，代入裂隙内空气和裂隙周围岩土的介电常数和体积分数，即可得到等效介电常数εeff，为了更好地体现出随机效果，将εeff加上随机变化δε(δε满足高斯分布)：

εfra=εeff+δε

(12)

式中:εfra即为裂隙的等效介电常数，赋予介电常数后绘制成的裂隙带(图4),含有35条裂隙，分四层，倾角为45°,εfra=5。

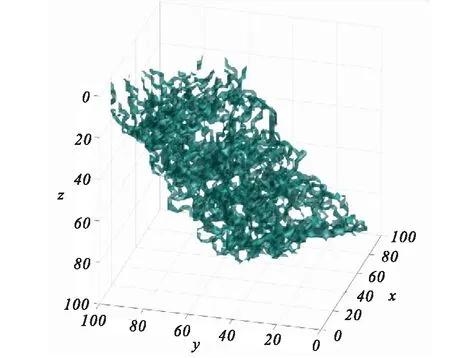
图4 Bruggeman等效处理后的裂隙带Fig.4 Fissure belt after satisfying Bruggeman equivalent theory

1.5 裂隙带岩土背景随机化处理

将复杂非均匀介质中的非均匀体看成一个空间随机过程，用统计学方法描述介质非均匀性所形成的非均匀分布就是随机介质模型[13]。由于土壤颗粒的组成及排列方式复杂，还有水分、有机质和矿物质等原因的影响，所以随机介质模型可以更准确地描述实际岩土背景的随机非均匀性分布，即：随机介质模型m(k)为均匀介质mi(k)和随机扰动所δm(k)组成(δm(k)满足高斯分布)，描述随机介质模型的基本思路描述如下：

m(k)=mi(k)+δm(k)=mi(k)[1+f(k) ]

(13)

式中：三维空间位置矢量表示为k=(x,y,z)；用f(k)代表这种随机介质的相对扰动的特征，其中f(k)=δm(k)/mi(k)。

对于f(k)的选择，采用了小尺度非均匀性的椭球式混合型自相关函数：

(14)

式中：r是代表模糊度因子(当r=0时为高斯型椭圆自相关函数，当r=1时为指数型椭圆自相关函数，r介于两者之间的，则为混合型自相关函数)；a、b、c分别代表x、y、z方向的自相关长度；再用式(15)作傅里叶变换，得到能量谱密度函数：

R′ (k)=‖F(k)‖2

(15)

式中:k=(kx,ky,Kkz)再加入随机相位φ(k)，变换后得到功率谱函数：

(16)

对公式(16)中F′ (k)进行傅立叶逆变换，从波数域变换到空间域的R(x,y,z),得到随机等效背景模型(图 5),均匀介质mi(k)=5，x、y、z方向的自相关长度A=5、B=5、C=5,模糊度r=0.5。

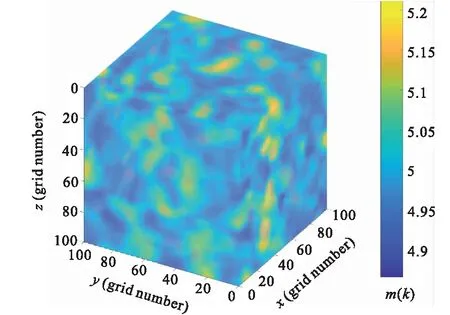
图5 随机等效处理后的背景介质Fig.5 The medium after satisfying the stochastic equivalent media theory

2 模型实例正演

图6所示为一个实例模型，模型大小为5 m×5 m×5 m，网格数为200×200×200，空间网格步长为0.025。模型背景分三层，第一层模拟表层土壤，厚2 m，介电常数平均值为10；第二层模拟湿润粘土层，厚2 m，介电常数平均值为15；第三层模拟基岩，厚1 m，介电常数平均值为4。所有层面背景自相关长度A=5,B=5,C=5,模糊度r=0.5，背景电导率为0.01 s/m。第二层内的裂隙带大小为5 m×1.25 m×2 m，倾角为38°，裂隙占裂隙带体积的20%，背景介质占裂隙带体积的80%。

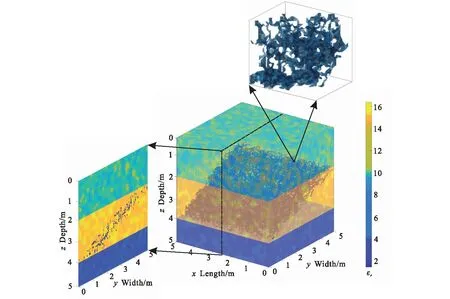
图6 在随机背景中的分形等效裂隙带模型Fig.6 Fractal equivalent fracture belt model in random background

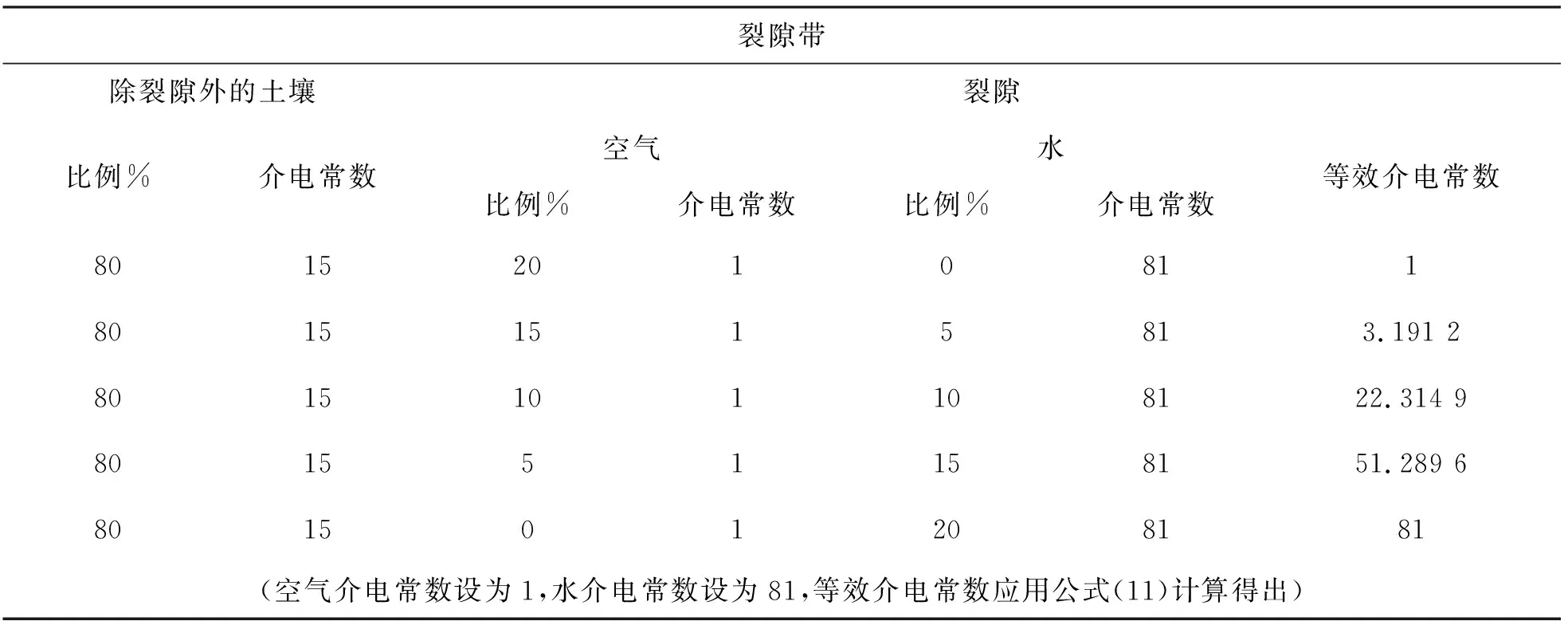
表1 不同含水率下裂隙带的Bruggeman等效介电常数

从0%到20%取5种含水率，计算裂隙的Bruggeman等效介电常数，如表 1所示。将5种等效介电常数赋值给裂隙，并对其进行探地雷达正演模拟。

探地雷达(GPR)波脉冲激励源的中心频率为100 MHz，时间步长为0.05 ns，时窗长度为120 ns。正演模拟得到响应结果后去除直达波，如图7所示，

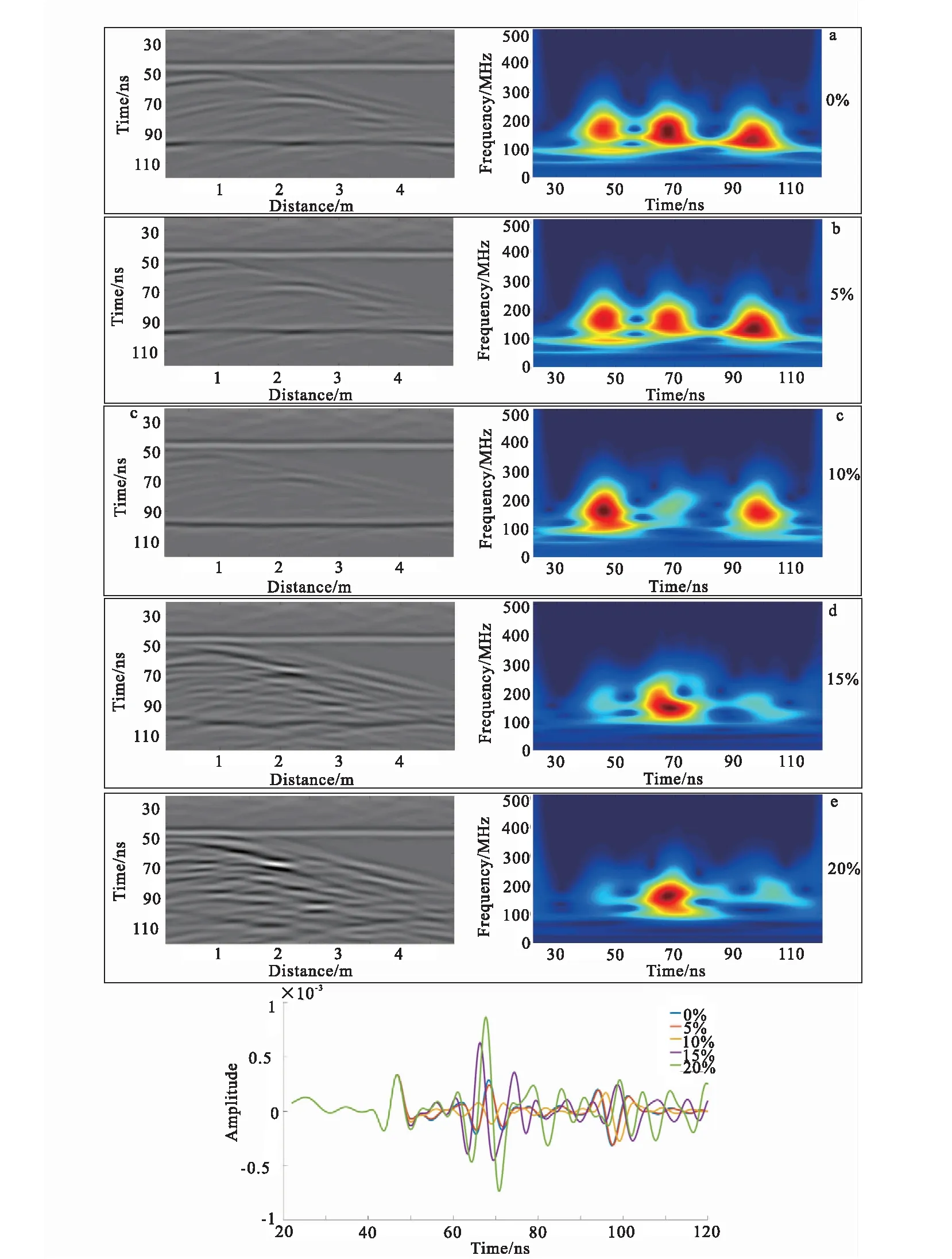
图7 不同含水率模型的探地雷达模拟响应结果Fig.7 Numerical simulation of GPR with different moisture content

左侧图7(a)～图7(e)依次为0%、5%、10%、15%、20%含水率的探地雷达正演响应结果。在图7(a)～图7(e)中均可观察到随机背景造成的微弱扰动，除图7(e)(含水率20%)外，分界面均较为清晰；在裂隙带区域，由于内部介质比较复杂，电磁波传播时的经历多次反射和绕射过程，双曲线波形较为散乱，同相轴更为模糊，但是仍能分辨出裂隙带的位置和形状；由于第二层介质介电常数为15，对比图7(a)～图7(e)可发现，含水率为10%时(图7(c)，左)，介电常数与背景较为接近，裂隙带造成的波形变化较小；裂隙带与背景的介电常数相差越多，波形扰动就越大，尤其当含水率为20%时(图7(e)，左)，也就是裂隙内充满水的情况下，裂隙带造成的混乱波形掩盖了第二层分界面。

取2 m位置处单道记录进行S变换，得到5种含水率响应的时频图，如图7所示，右侧图7(a)～图7(e)依次为0%、5%、10%、15%、20%含水率响应结果的S变换时频图。由于S变换压制了噪声，减弱了随机背景的影响，使得两层分界面和裂隙带的异常均清晰可见。对比图7中图7(a)～图7(e)，可以发现含水率为10%时(图7(c)，右)，由于裂隙带介电常数与背景较为接近，两层分界面的异常明显强于裂隙带异常；含水率变低或变高，即介电常数与背景差异越大，裂隙带异常就越明显；且含水率较高时(图7(d)和图7(e)，右)，裂隙带异常明显强于分界面异常值。

不同含水率模型响应的2 m位置处单道记录(图7(f))也佐证了上述规律。在前50 ns，不同含水率模型响应基本一致；在含水率为10%时，裂隙带位置(68 ns附近)振幅变化相对较小，而含水率越低或越高，振幅变化越大，异常越明显。

由Bruggeman等效介质理论计算可得出介电常数与第二层背景相等(ε=15)时，含水率为8.63%，此时裂隙带基本无响应。将不同含水率和其时频图中裂隙带处的最大幅值进行三次多项式拟合处理，得到的拟合曲线和公式如图8和公式17所示。通过时频变换，我们得到了该模型下的裂隙带含水率与正演响应的定量关系，根据此拟合公式，可用响应估算含水率。

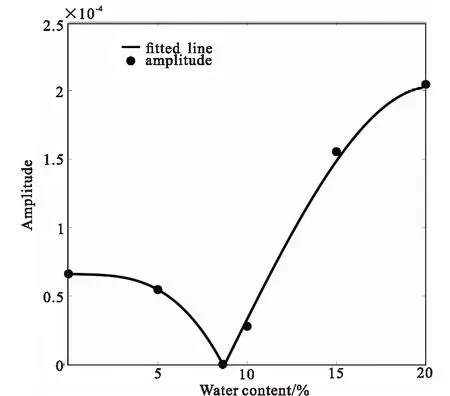
图8 不同含水率时频图在裂隙带位置最大幅值的曲线拟合Fig.8 Curve fitting of the maximum amplitude of the time - frequency pattern with different water content

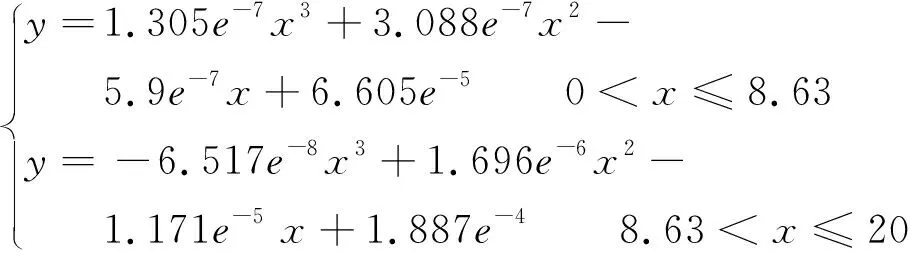
(17)

根据不同含水率时频图(图7(a)～图7(e)，右)中裂隙带异常最大值位置的走时，可以计算出该道裂隙带中心深度，误差估计如表2所示，可以发现，响应结果对裂隙带深度的估计较为准确。

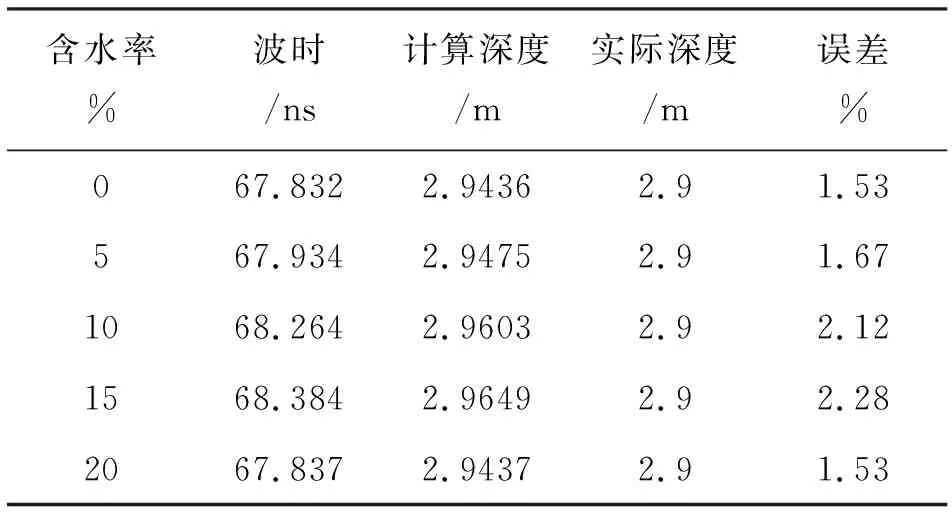
表2 不同含水率模型响应结果的裂隙带深度误差估计Tab. 2 The errors estimation of fissure belt for response results of different moisture model

3 结论

三维Koch分形曲线具有联通性、随机性和自相似性，通过Koch曲线模拟的骨架表现了裂隙分布的分维特征；对裂隙中空气和水应用Bruggenman等效介质方法，得到多种含水率的岩土介电常数，满足了不同情况和计算效率的需求；应用随机等效介质方法使岩土背景呈现多尺度的随机性，模拟了真实岩土介质的复杂状况。

对不同含水率下的裂隙带模型进行GPR数值模拟后，可以发现裂隙带含水率对响应波形的影响较大。裂隙等效介电常数与背景相差越多，裂隙带的响应越明显，当裂隙内充满水后，噪声甚至可以掩盖分界面波形。对响应进行S变换(ST)后分析其时频特征，既压制了混杂的噪声，又可拟合出该模型下的含水率-响应曲线。根据此曲线的定量关系，可通过响应估算含水率。最后进行的裂隙带深度的误差分析,证实了数值模拟及时频分析结果的可信性。此建模、探地雷达响应数值模拟及信号时频分析方法可以为岩土体中软弱带及含水裂隙带的探测提供参考。