小波变换与SVD结合消除随机噪声的研究及应用

宋 林

(中国石油化工股份有限公司 石油物探技术研究院，南京 211103)

0 引言

地震资料中的噪声通常分为两类：①随机噪声(无规则干扰)；②相干噪声(规则干扰)。针对随机噪声而言可以按照是否满足高斯白噪的条件分为高斯随机噪声和非高斯随机噪声。随机噪声在地震资料中与地震有效信号相伴相随，当随机噪声具有相对较高的能量时，将对地震资料处理中的NMO速度分析以及静校正等产生不利影响，最终使偏移成像的效果欠佳，给后续的地震解释工作带来诸多不利影响。因此随着多年的方法研究和技术发展，技术人员设计了多种不同的随机噪声消除方法， F-X域反褶积、中值滤波、多项式拟合等，但这些方法总体可分为两大类：增强信号和压制噪声[1]。诸如F-X域反褶积、多项式拟合以及径向滤波等均属于增强地震有效信号类；中值滤波和τ-P域滤波则属于压制噪声类。

F-X域反褶积[2]是基于前后两道地震记录的有效信号部分相似性假设的基础，在频率域内利用前一道信号预测后一道信号，或者后一道信号预测前一道信号，以此增强信号压制噪声。此方法在实际处理中应用广泛，是增强信号连续性的选择，但是该方法也存在两点不足：①在增强信号的同时也会使相干噪音得到加强；②在地震信号的高频段信噪比相对较低，该方法去噪处理后易使高频段信号产生畸变。中值滤波是非线性滤波的一种，英国的D.R.K.Brownrigg[3]提出了加权中值滤波； Loupas[4]进一步发展为自适应加权中值滤波；刘财等[5]将其应用于地震资料噪声压制方面，取得了较好的效果，此方法主要使用空间中值滤波对叠后剖面进行噪音压制。多项式拟合方法由余寿朋[6]提出的，该方法基于地震有效信号的空间相似性，通过多道记录相关确定有效同相轴的位置，得出有效信号的模型道，进而根据相关系数完成有效信号在时间和振幅大小的拟合，以增强有效信号的连续性，压制随机噪声提高信噪比,但对于随机噪声相对严重的情况下，有时会出现假的同相轴。另外，多项式拟合方法应用于没有断层或断层不发育的地区，处理后同相轴的连续性大大提高，有效信号获得明显提升。而对于起伏变化剧烈，断层发育的区域，会造成同相轴时空位置发生改变。

小波变换是一种应用非常广泛的时频分析方法，自提出以来，在理论研究和实际应用中不断得到改进，具有优良的时频分辨率特性。方形矩阵的奇异值分解(Singular Value Decomposition，SVD)首先由Beltrami[7]和Jordon[8]各自独立地与1873年和1874年发现。奇异值分解直到20世纪30年代才被推广到长方形矩阵。随后矩阵计算大师Gene Golub[9]进一步发展了奇异值分解。SVD是线性代数中最重要的工具之一，在统计分析、信号处理、故障检测和数据降噪等方面都有重要应用。

小波变换在地震资料去噪方面应用非常广泛，SVD在信号处理领域有其独特本领,但是由于小波变换去噪存在阈值难以确定的不足，使去噪结果存有去噪过度或去噪不足。而SVD去噪的主要缺点是信号方向及主元素的个数确定困难。因此笔者通过分析小波变换和SVD方法的特点，将两者结合，相互弥补。

1 方法原理

利用连续小波变换与SVD相结合的去噪方法是：先使用连续小波变换(如Morlet)将要分析处理的地震信号分解到各个不同的尺度中，得到的每个尺度相应的小波系数，这些不同尺度的小波系数就组成了一个满足SVD分解的一个矩阵，也叫做相空间。

平方可积的信号函数f(t)∈L2(R)，ψ(t)为一个确定的基本小波函数，令：

(1)

式中：a,b∈R，a≠0。则称函数ψab(t)为由小波母函数ψ(t)生成的依赖于尺度参数a和平移参数b的连续小波，那么就可以称

(2)

为被分析信号f(t)的连续小波变换[10],Wf(a,b)是变换后得到的小波系数。其逆变换公式为式(3)[11]。

(3)

采用连续小波变换对单道信号进行尺度分解，使用morlet小波作为基小波，所分解的尺度数为M，即每道信号分解后得到一个行数为M，列数为每道的采样点数N的小波系数矩阵A，即A为M×N。

针对上述小波变换得到的M×N的矩阵A，无论其是否奇异，SVD分解总能唯一的将其分解为M×M元素的正交阵U与M×N的对角阵W和一个N×N的正交阵V的乘积表示为[12-15]：

(4)

对新组成的相空间采取SVD分解后，就会将被分解信号所含有的频率的每一个特征分量分解到各个相应的具有正交关系的子空间中去。

由于小波变换后的各尺度系数上的信号具有极强的相似性，从而避免了传统SVD技术中的方向扫描过程，更有利于信号与噪声的分离。

奇异值的选取原则由奇异熵确定。在解释什么是奇异熵之前先给出奇异谱的定义式子：

(5)

则由σi(i=1,2,…,p)求得的这里的一系列数值就组成了经由连续小波变换后的矩阵做SVD分解后的所需要的奇异谱。λi(i=1,2,…,p)是SVD分解后得到的奇异值。奇异熵的概念是根据奇异谱得来的，它是用来表示地震信号中量的变化的规律的，奇异熵[16,17]的表达式为式(6)。

(6)

式中：k表示的是所求得的奇异熵所在的位置，是在第几阶上；ΔEi则表示的是这里求得的奇异熵在相应位置上的i处的变化的多少，可以利用公式(7)求得。

(7)

奇异熵对地震资料信号的信噪比反映非常敏感。若地震信号没有受到外界任何干扰(当然了这是理想的状态)，求得的奇异谱在相对较低的阶次就能包含全部信息，此时的奇异熵将会是稳定在在一个比较固定的数值上；若求得地震信号的奇异熵表现为明显的上升，就说明了这段地震信号含有宽频率的噪声。因此根据求得的奇异熵对SVD后得到的奇异值进行筛选，再对信号进行SVD逆变换和小波逆变换重构，从而实现去噪。奇异熵的应用使主元素个数的选取具有数理依据，减少了去噪过程中的过扼杀或过保留的几率。

去噪处理的具体步骤如下：

1)以单道地震信号作为输入。

2)使用morlet小波对输入的单道地震信号进行连续小波变换，得到变换后尺度为M(本文选择尺度数为90°)，N为采样点数的小波系数矩阵A。

3)对小波系数A=M×N的矩阵进行SVD分解，得到相应的90个奇异值。

4)利用公式(5)、式(6)和式(7)计算奇异谱与奇异熵。

5)通过奇异熵筛选出需要SVD逆变换的奇异值，进行小波系数矩阵重构。

6)对重构后的小波系数矩阵进行小波逆变换，得到去噪后的信号，并输出结果。

流程图如图1所示。

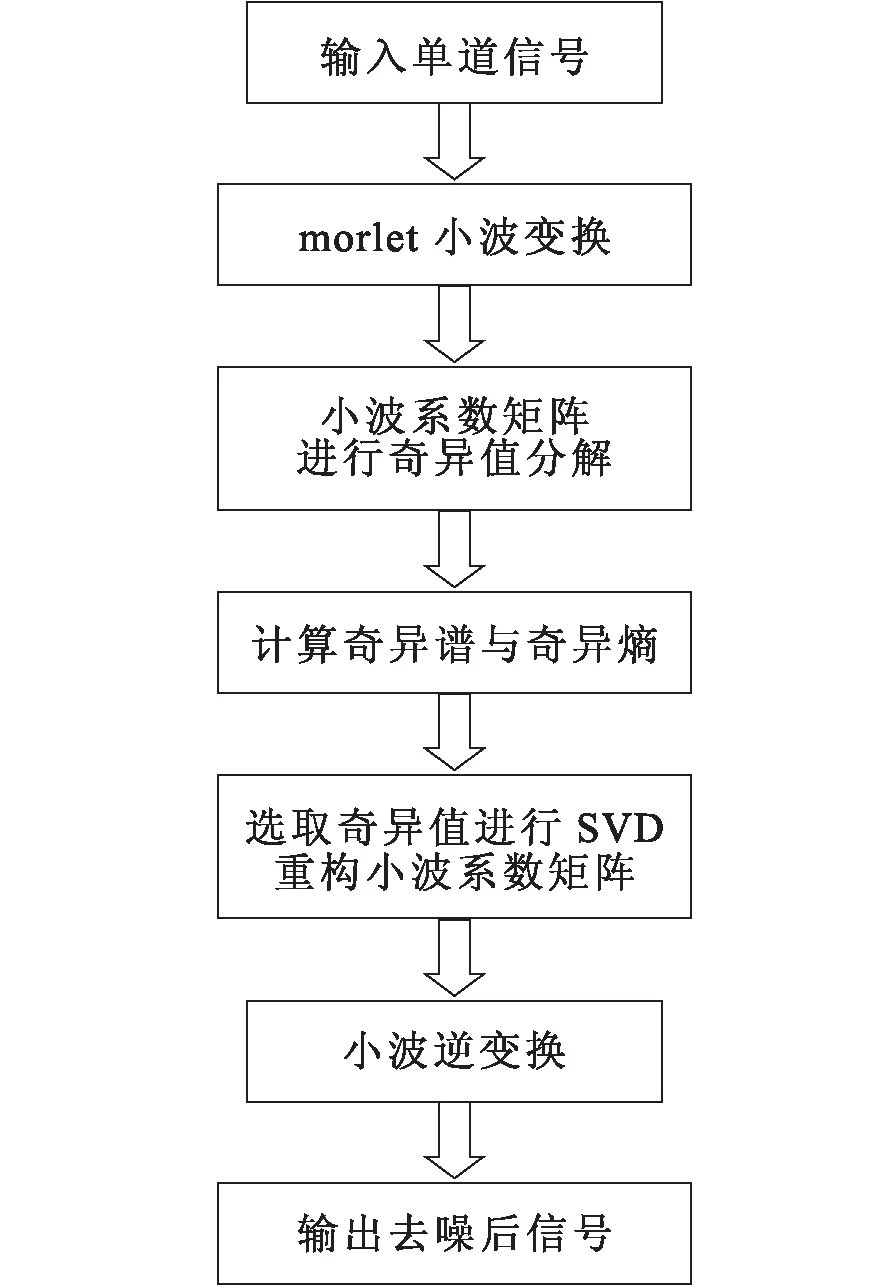
图1 连续小波变换-SVD去噪流程图Fig.1 The denoising flow of CWT-SVD

2 模型数据测试

图2为一个模型的单炮记录，使用40 Hz的雷克子波正演，共有三个反射层，其中第三层反射较弱。

图2 单炮记录Fig.2 The shot gather

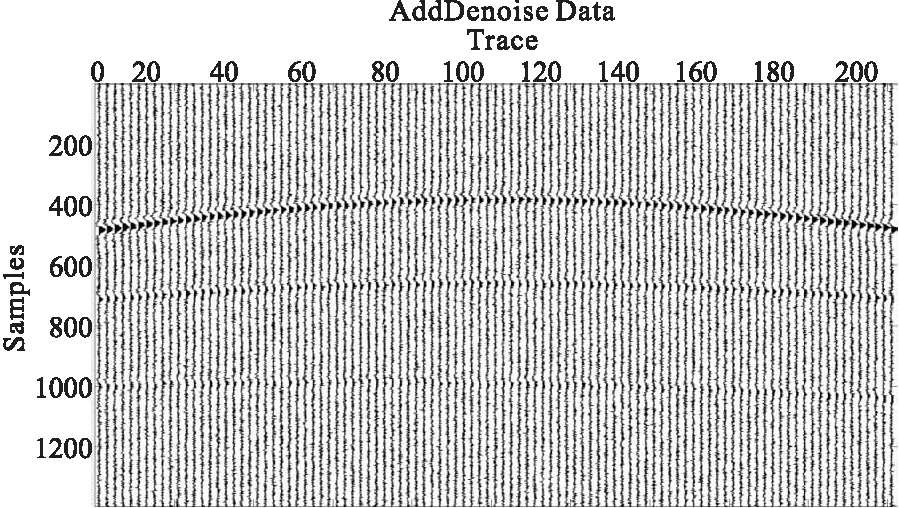
图3 加噪后单炮记录Fig.3 Shot gather with noise

图3表示为图2的单炮记录加上随机噪声之后的含噪记录，从图3中可以看出，背景的随机噪声与单炮记录的第三个反射同相轴的能量相同，使得其基本淹没在背景噪声中，不容易辨别。使用本文方法对背景随机噪音进行压制的单炮记录(图4)，从图4可以清楚地看到同相轴变得更加清晰，尤其是第三个相对较弱的同相轴也比较清晰地呈现出来，并且整个记录的背景相对图3有了明显地减弱，信号得到增强，提高了信噪比。图5表示的是图3与图4相减得到的差剖面，从中基本看不到明显的有效信号，所以本文的方法对背景随机噪声的去除是有效的，能够提高道集的信噪比，达到去除噪声保护弱信号的目的。

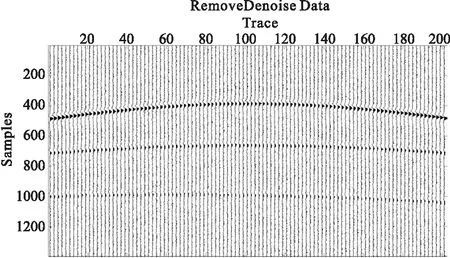
图4 去噪后单炮记录Fig.4 The shot gather after denoising

图5 图3单炮去掉的噪音Fig.5 The removed noise of shot in Fig 3

图6 含噪叠加剖面Fig.6 The stack with noise

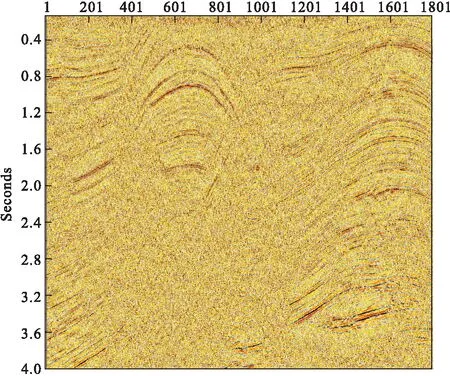
图7 图6 去噪后叠加剖面Fig.7 The stack of Fig 6 after denoising

图8 图6含噪叠加剖面去掉的噪音Fig.8 The removed noise of Fig 6

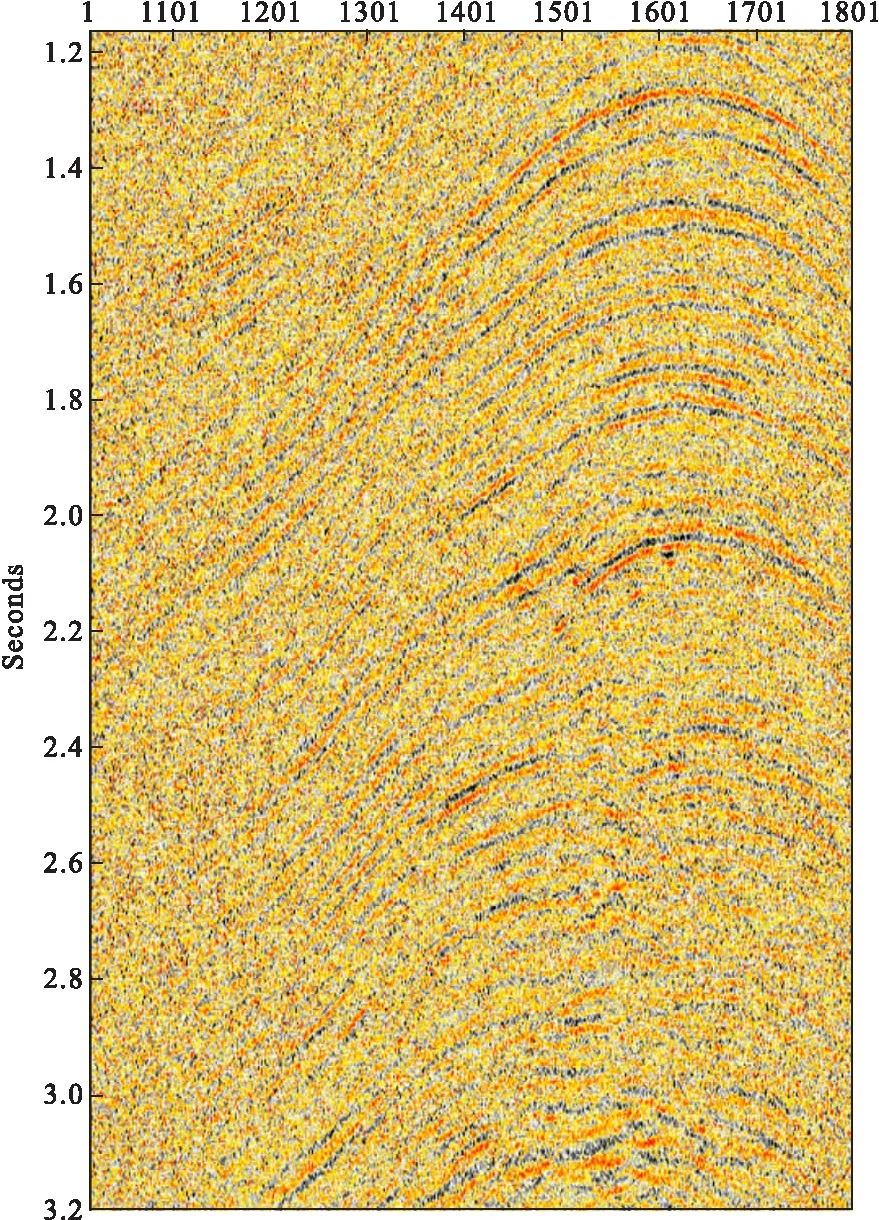
图9 图6的局部放大Fig.9 The partial enlarged of Fig 6

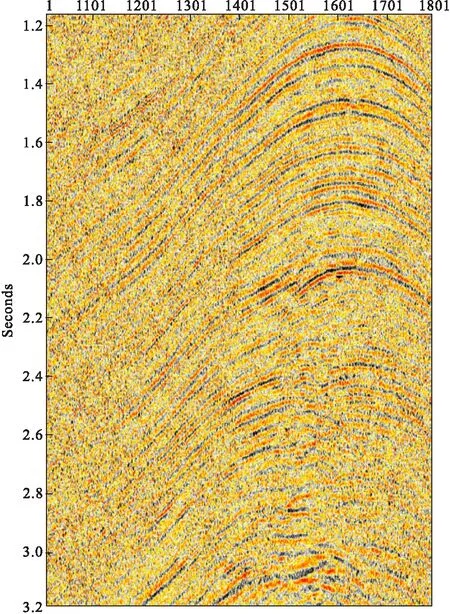
图10 图6的局部放大Fig.10 The partial enlarged of Fig 6

图11 图8局部放大Fig.11 The partial enlarged of Fig 8

3 实际资料应用

实际资料是来自我国西部地区某工区的资料，资料噪声特征是随机噪声比较发育。图6为F-X反褶积处理后的叠加剖面，可以看出在剖面中仍然残留部分随机噪声，影响了剖面的质量。图7为去除后的结果，从图7中可以看出信噪比有了明显提高，淹没在随机噪声中的同相轴得到了较好地增强，同相轴更加连续，信噪比明显提高，整个剖面的质量有了提升。图8为去噪前、后资料的差剖面，从剖面上看基本没有损失有效信号，绝大部分是噪音，与模型验证的结果一致。图9为含噪资料的局部放大显示，图10为消除噪音后的局部放大显示，图11为相对应的图9与图10的差剖面。从以上得到的结果可以看出，此小波变换与SVD相结合消除随机噪音的方法在去除随机噪音方面是有效果的，能够在去除噪音的同时基本不损害有效信号，进而提高资料的信噪比。

4 结论

通过观察对比以上模拟单炮记录与实际叠加剖面两组去噪前后的资料，我们得到以下结论：

1)连续小波变换和SVD分解相结合的去除随机噪声的方法是有效的。

2)对于增强有效波同相轴的连续性方面相比F-X域反褶积具有较好的效果。

3)此小波变换与SVD相结合消除随机噪音的方法对于资料的浅层和深层都有较好的效果，且保真度较好。