考虑交通拥堵的出租车市场均衡模型
2019-01-16田丽君詹晓斌
田丽君, 詹晓斌
(福州大学 经济与管理学院,福建 福州 350116)
0 引 言
出租车是城市公共交通不可或缺的一部分,它能提供24小时、点对点的服务,具有灵活、舒适、私有等优点。2016年11月1日,《网络预约出租汽车经营服务管理暂行办法》的正式实施标志着网络预约出租汽车(简称网约车)的合法化。网约模式中司机和乘客通过打车软件进行交流,避免了空驶出租车搜索的盲目性,降低了信息不对称,减少了无效搜索,从而缩短了司乘双方的等待时间,提高了出租车资源的利用效率。
1972年,G.W.DOUGLAS提出了出租车市场集计模型来刻画出租车市场均衡[1]。随后,A.S.D. VANY运用G.W.DOUGLAS的模型进一步研究了不同环境下的出租车市场,发现最大有效需求只在零利润条件下取得[2]。H.YANG等假设出租车以最小化预期成本为目标搜索乘客,率先提出了出租车网络模型[3]。随后,H.YANG等通过考虑拥挤外部性进一步扩展了模型[4]。边扬等研究了城市出租车网络的运营特性与不同状态下的出租车路径选择规律,分析了固定需求条件下出租车运营网络的供需平衡关系,建立了城市出租车网络平衡模型[5]。钱勇生等通过对出租车容量的集合模型的改进,运用交通小区调查的结果,计算现有出租车的容量[6]。慕辰等用仿真的方法研究了出租车不同空车策略对系统性能的影响,发现基于历史信息的空车策略能够有效提高系统运营效率,而提供呼叫服务对于出租车运营方是不利的[7]。罗端高等考虑需求分布的影响,分析了出租车网络的运营特征与出租车在不同状态下的路径选择行为,构建了相应条件下的城市出租车网络平衡模型[8]。杨英俊等先后构建了出租车运量投放计划模型和出租车保有量预测模型[9-10]。T.YANG等用对数线性联立方程模型来估计考虑司乘之间搜索阻力的柯布-道格拉斯型双向搜索与匹配函数中的规模收益问题[11]。
2010年后,互联网+技术和共享经济的快速发展起来,网络预约出租车这种新型打车方式也备受乘客的青睐。打车软件出现后对出租车市场供需平衡的影响也引起了许多学者的注意。度巍等探讨了使用手机召车软件的派遣服务模式下出租车系统中各参数变化对乘客等待时间的影响[12]。曹祎等基于打车软件使用率建立了模型,算例表明,在出租车运营时间及乘次固定的条件下,模型能得出不同打车软件使用率与总运营里程、总体运营速度及空驶率之间的对应关系[13]。接着,曹祎等又对手机召车软件的市场渗透率进行了研究[14]。F.HE等分析了隐藏目的地信息与出租车系统性能的关系[15]。X.WANG等用集计方法创建了单一打车软件市场条件下的市场均衡模型,并分析了平台的收费策略对市场均衡的影响[16]。
上述文献分别阐述了传统巡游模式下的出租车市场均衡特性、出租车规模确定和打车软件背景下的乘客等待时间、打车软件使用率、手机召车软件市场渗透率以及打车软件平台的收费策略等问题。打车软件出现后,与传统巡游模式的盲目搜索不同,网约车司机能够精确获知乘客的位置信息,在不受拥堵干扰的情况下能够更加快速地接到乘客,因而在等待时间相同的情况下,网约车的服务半径和匹配效率会明显高于巡游车。但在实际生活中,城市局部拥堵已经变得非常普遍,拥堵产生的不确定性会使得出租车司机刻意避开拥堵路段,有针对性地挑选乘客,进而影响出租车司机的模式选择、乘客的等待时间和司乘双方的匹配率等。如果忽略交通拥堵,将会导致构建的出租车市场均衡模型无法反映现实生活中的很多真实特点,从而不能准确地预测均衡结果。基于这一考虑,笔者在以往研究的基础上,构建了考虑交通拥堵的包含巡游车和网约车的出租车市场均衡模型,并通过算例分析了两类平均行驶速度对乘客等待时间、乘客占比、出租车空驶时间以及平均乘客等待时间或社会福利的影响。
1 基本模型
考虑包含巡游车和网约车的出租车市场,根据司乘沟通的方式把出租车市场分为两种模式:采用路边扬招进行沟通的模式称为巡游模式,对应模式下的出租车和乘客分别称为巡游出租车(简称巡游车)和扬招乘客;采用打车软件进行沟通的模式的称为网约模式,对应模式下的出租车和乘客分别称为网约出租车(简称网约车)和网约乘客。
1.1 巡游模式和网约模式的匹配效率
一般来说,司机和乘客的匹配效率(meeting efficiency)由候车的乘客与空驶出租车在单位时间内的匹配成功率来衡量。在传统的巡游出租车市场中,司机与乘客之间无法进行信息交流,双方完全凭借主观经验进行搜索,因此司乘双方均需花费大量的时间来寻找对方。根据H.YANG[17]等人的研究,司机和乘客之间的匹配率(meeting rate)取决于候车的乘客数量和空驶巡游车的数量,表示为:
(1)

打车软件作为司乘双方的沟通媒介,它的使用使司乘双方能提前获知对方的具体信息,大大降低了司乘之间的信息不对称。但是,这并没有完全消除司乘之间的匹配阻力(matching friction)。因为,匹配阻力的大小很大一部分是由匹配面积决定的,匹配地点的面积越大,司机越难找到乘客,匹配就越困难,反之,越容易。一般情况下,司乘双方通过打车软件沟通上车的地点,使得匹配的面积大大缩小,但并没有达到完全精确(面积为0)。因此,网约模式下的司乘之间的匹配阻力并不为0。类似地,网约模式下司乘之间的匹配率可表示为[17]:
(2)

为了更具体地分析司乘之间的匹配特性,假设两种模式的匹配函数满足柯布-道格拉斯型生产函数,即:
(3)

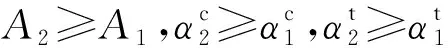
(4)
式(4)总成立,体现了网约模式在匹配效率方面的优势。
1.2 乘客等待时间与出租车空驶时间
根据H.YANG[17]等的研究,模式i的乘客等待时间可由等车乘客数量和匹配率表示为:
(5)
同样地,模式i的出租车等待时间也可以由空驶出租车的数量和匹配率表示为:
(6)
1.3 乘客与出租车选择行为
假设乘客按照预期出行成本的大小来选择打车方式,且乘客选择打车方式的随机性满足二重指数(Gumbel)分布,则乘客的选择行为可以表示为:
(7)

(8)
(9)
式中:P为出租车费用;L2为出租车载客时的平均行驶里程;v2为载客出租车的平均行驶速度;β1和β2分别为乘客等待时间成本与出行时间成本。
类似地,假设空驶出租车按照自己的出行效用来选择服务模式,且空驶出租车选择服务模式的随机性同样满足二重指数(Gumbel)分布,则空驶出租车选择服务模式的行为可以表示为:
(10)
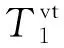
(11)
(12)
式中:β3为出租车单位时间运营成本,与出租车的运营状态(载客或者空驶)无关。此外,由于出租车规模是恒定的,因此单位时间内出租车服务总时间由出租车规模决定,即服务时间满足约束如式(13):
(13)
2 出租车市场均衡及其求解
出租车市场达到均衡状态时,每种服务模式下空驶出租车刚好满足选择该种服务模式的乘客的出行需求,如式(14):
(14)
联立式(1)~ 式(14),化简整理后,可得到出租车市场均衡状态的条件如式(15)~ 式(20):
(15)
(16)
(17)
(18)
(19)
D1=D-D2
(20)
不难发现,式(15)~式(20)是非线性和非凸的,所以不存在使均衡解收敛的算法。根据X.WANG[16]等人的工作,当稳定的均衡解存在时,可以用定点迭代算法求出一定收敛条件下的均衡解:

(21)
(22)
(23)
(24)
(25)

3 算 例
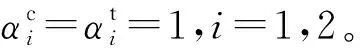
根据滴滴媒体研究院发布的《2016智能出行大数据报告》,取v2=20 km/h,首先分析平均行驶速度v1对乘客等待时间、乘客打车方式和出租车空驶时间的影响,见图1。

图1 v1对乘客等待时间与乘客打车方式的影响Fig. 1 Influence of v1on passenger’s waiting time and the hailing taxi mode of passenger
从图1(a)可以发现,在其他条件不变的情况下,随着空驶网约车平均行驶速度v1的持续提高,网约乘客的等待时间大幅下降,扬招乘客的等待时间小幅降低,基本保持不变。但网约乘客的等待时间相对于扬招乘客的等待时间是逐步减少的。这说明,在较拥堵的区域(算例中v1≤18.2 km/h时),使用打车软件叫车的等待时间高于路边直接叫车的等待时间,而随着道路变得通畅(v1≥18.2 km/h时),使用打车软件叫车的优势便逐步显现。这一点在图1(b)中得到了直观的体现,扬招乘客的占比随着v1的增大逐渐减少,网约乘客的占比随着v1的增大持续提高。当v1≥18.2 km/h时,网约乘客的占比会高于扬招乘客的占比。
图1从乘客的角度分析了空驶网约车平均行驶速度v1的影响,图2则从出租车的角度进行分析。

图2 v1对出租车空驶时间的影响Fig. 2 Influence of v1on the vacant time of taxi
从图2可见,随着v1的增加,网约车的等待时间不断减小。显然,一方面是由于接单后的空驶时间减少,另一方面是由于网约乘客占比增加而提高了匹配率,因此,网约车的运输效率得以提升。对于巡游车来说,随着v1的增加,扬招乘客的占比不断减少,因而扬招模式的匹配率也随之降低,进而导致巡游车的搜索时间不断增加。
取v1=20 km/h,图3和图4分别给出了载客出租车平均行驶速度v2对乘客等待时间、乘客打车方式和出租车空驶时间的影响。
从图3(a)中可以发现,随着道路交通状况的不断改善(v2持续增加),巡游车和网约车的运输效率不断提高,网约乘客和扬招乘客的等待时间均呈下降趋势。在交通比较拥挤时(即v2≤22 km/h时),网约模式中司乘双方因为能更精确地掌握供需的分布情况,因而匹配率较高,网约乘客的等待时间小于扬招乘客的等待时间。基于此,网约乘客的占比也高于扬招乘客,见图3(b)。当道路逐渐变得比较通畅时(v2≥22 km/h),由于出租车运输效率得到提高,空驶出租车数量(或出租车供给)也逐渐增加,网约模式所表现出的信息优势逐渐消失,再加上网约车确认订单后还需花费额外的时间去搜索和搭载乘客,因而网约模式匹配率逐渐降低,网约乘客的等待时间在下降到一定水平之后就基本保持不变。与此不同的是,扬招模式的匹配率则因为空驶出租车数量的增多而不断提高,因而扬招乘客的等待时间依然不断下降。此时,选择网约模式的乘客占比明显低于扬招模式(见图3(b))
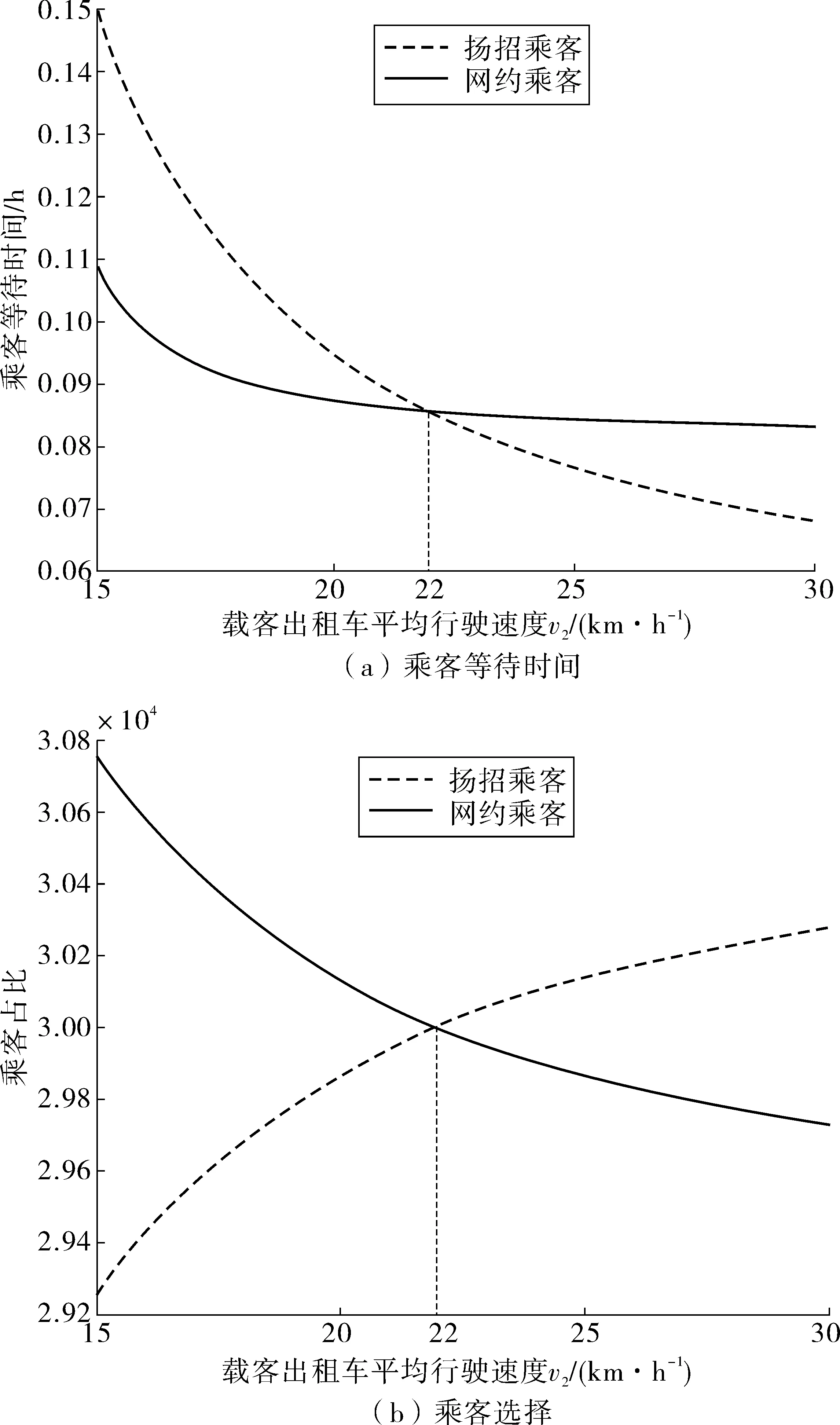
图3 v2对乘客等待时间与乘客选择的影响Fig. 3 Influence of v2on passenger’s waiting time and the hailing taxi mode of passenger

图4 v2对出租车空驶时间的影响Fig. 4 Influence of v2on the vacant time of taxi
图4中,随着平均行驶速度v2的不断提高,巡游车和网约车的运输效率均持续增加,相对于有限的乘客需求,单位时间内道路上的空驶出租车数量与候车乘客数量的差值持续扩大,空驶出租车越来越难找到乘客,因此,巡游车和网约车的空驶时间均不断增大,但网约车的空驶时间上涨幅度明显大于巡游车。这主要是因为,当v2≤22 km/h时,由于网约乘客的占比较高,因而网约车的空驶时间较短;但随着道路环境的持续改善,当v2≥22 km/h时,扬招乘客的占比超过网约乘客,导致网约车比巡游车更难找到乘客,所以,网约车的空驶时间慢慢多于巡游车。

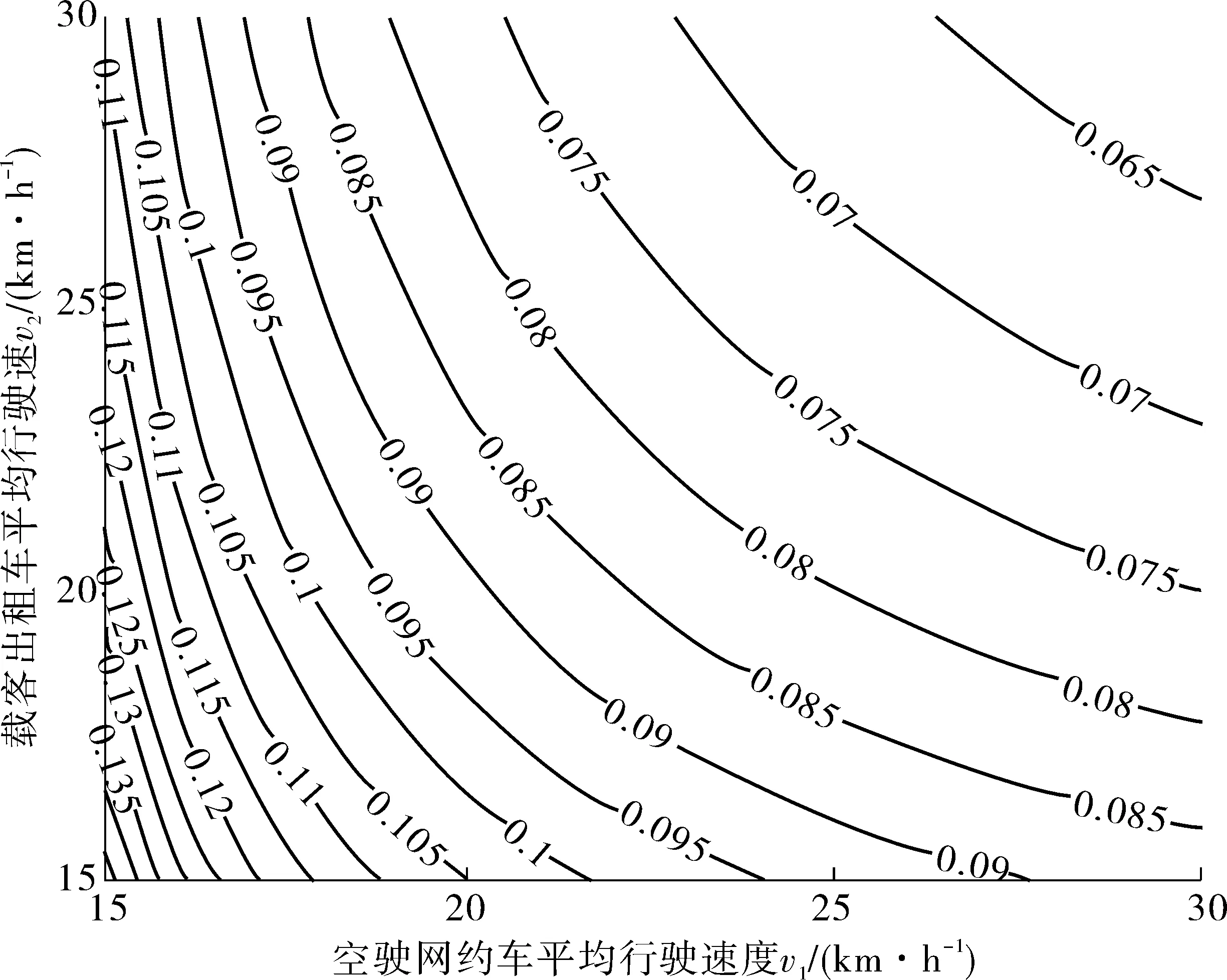
图5 v1和v2对平均乘客等待时间的影响Fig. 5 Influence of v1andv2on average passenger’s waiting time
4 结 论
通过考虑交通拥堵这一现实生活中普遍存在的现象,对包含巡游车和网约车的出租车市场进行了分析,创建了考虑交通拥堵的城市出租车市场均衡模型,并用定点迭代算法求解了模型,最后通过一个算例对模型中的相关参数进行了分析讨论。研究发现,一方面,网约车空驶平均速度的增加能提高网约车的运输效率,使得网约乘客的等待时间不断降低,但对巡游车的运输效率没有显著影响;扬招乘客的等待时间并未发生太大变化,在v1较低时,网约乘客占比低于扬招乘客,网约车空驶时间高于巡游车,在v1较高时,网约乘客占比高于扬招乘客,网约车空驶时间低于巡游车。另一方面,出租车载客空驶平均速度v2增加能提高出租车的整体运输效率,降低所有乘客的等待时间,进而使得单位时间内道路上的空驶出租车数量与候车乘客数量的差值持续扩大,巡游车和网约车的空驶时间都持续增加,但网约车的空驶时间上涨幅度明显大于巡游车。同时,由于扬招乘客的等待时间相对于网约乘客是下降的,因而扬招乘客占比不断上升,网约乘客占比不断下降。此外,提高两类平均行驶速度均能降低平均乘客等待时间,从而提高出租车系统的社会福利,但在路网比较拥堵时,提高平均车速能使出租车系统的社会福利得到更大的提升。研究结果旨在为乘客出行选择及政府部门制定网约车相关政策提供参考依据。
