基于K-S检验法和ALTA的IGBT模块可靠性寿命分布研究

2019-01-16吴华伟叶从进聂金泉

重庆交通大学学报(自然科学版) 2019年1期

吴华伟，叶从进,2，聂金泉

(1. 纯电动汽车动力系统设计与测试湖北省重点实验室，湖北襄阳 441053；2. 武汉科技大学机械自动化学院，湖北武汉 430081)

IGBT是由功率场效应晶体管(MOSFET)和双极型功率晶体管(BJT)复合而成的一种电力电子器件，它结合了MOSFET和BJT的优点，具有输入阻抗高、功耗小、热稳定性好、驱动简单、载流密度大、通态压降低等优势[1-3]。随着科学技术高速发展，IGBT模块已广泛应用于各类电能转换装置、新能源发电、开关电源、变频器、牵引传动以及电动交通工具等领域[4-6]。

随着IGBT模块广泛应用，其寿命可靠性问题也越来越为人所重视。国内外学者进行了大量详细的研究。唐勇等[7]通过开展高温下IGBT功率循环实验，从而提出了一种通过监控压降变化来实现IGBT 模块可靠性在线评估方法，该方法操作简单且准确度较高，对于确保IGBT模块与整个装置长时间安全可靠地运行具有重要意义。米伟等[8]基于在线获取的IGBT模块特征量参数，提出了一种对IGBT模块可靠性评估的新方法，该方法预测精度较高、测量数据较易、能及时预警缺陷严重模块，从而为IGBT模块可靠性在线评估和寿命预测提供了参考依据。王彦刚等[9]对IGBT模块失效原因进行了分析，认为其寿命分布服从Weibull分布。

笔者针对IGBT模块寿命分布及可靠性进行了深入研究，通过ALTA对其加速寿命试验数据做了仿真分析，用实例证明了IGBT模块寿命数据服从对数正态分布的假设，且该方法可用于IGBT模块可靠性分析，为其复杂可靠性分析提供了一种简单、实用方法。

1 IGBT模块寿命分布理论

1.1 IGBT模块寿命正态分布理论假设

加速寿命试验是在保证失效机理不变条件下，通过把样品放在超出正常应力水平下进行的试验，是一种促使样品短期内失效的试验方法[10]。其目的是为缩短试验时间、提高试验效率、降低试验成本，利用高应力水平下寿命特征去外推正常应力水平下寿命特征[11-12]。因此在加速应力下IGBT模块寿命分布服从何种分布，那么外推正常应力下也一定服从相同的分布，故笔者作出如下假定。

(1)

式中：μ为对数均值；σ2为对数方差。

假定2：在正常温度应力水平S0和各加速应力(结温差)水平S1，S2，…，Sk下，IGBT模块的失效机理不变，其关系如式(2)：

(2)

假定3：对于IGBT模块，均值μi与所加的应力水平Si之间满足如下加速方程，如式(3)：

μi=a+bΦ(Si),i=0,1,…,k

(3)

式中：a,b分别为待估的加速参数；Φ(Si)为Si的某一已知函数。

假定4：失效概率遵循Nelson定理。1980年Nelson提出了著名的原理：样品残存寿命只与已累积的失效和当前应力有关，而与累积方式无关。即IGBT模块在加速应力Si下，工作ti时间后的累积失效概率Fi(ti)，等同于其在加速应力水平Sj，工作tj时间后的累积失效概率Fj(tj)，如式(4)：

Fi(ti)=Fj(tj)

(4)

1.2 IGBT模块寿命分布参数计算方法

对式(1)，对数正态分布所对应的密度分布函数如式(5)：

(5)

结合式(5)，IGBT模块的似然函数如式(6)：

(6)

式中：n为参与试验的样品总数；ti为失效时间。

对式(6)取对数求导，得似然方程，如式(7)：

(7)

利用数值方法求解上述得到的方程组，从而可得到参数μ、σ的极大似然估计。

2 实验仿真与结果分析

2.1 加速寿命实验数据分析

根据IGBT模块失效机理可得出，其失效原因是因为模块工作时产生的热量无法及时向外部空间释放，导致其温度迅速上升，发生热击穿，所以笔者选择结温差(IGBT芯片结温之间的差值)来作为IGBT模块加速寿命试验加速应力。

由刘宾礼等[14]的研究可知：GD50HFL120C1S型1 200 V/50 A的IGBT模块额定工作电流为50 A，导通电流在110 A以内时，其失效机理不变，因此笔者选取导通电流为80、90、100 A，由此得到了3组加速应力水平为70、90、100 K的试验数据，如表1。

表1 IGBT模块加速寿命试验数据Table 1 Accelerated life test data of IGBT module

为检验IGBT模块寿命是否服从对数正态分布，笔者通过MATLAB软件中的Normplot函数和Kolmogorov-Smirnov检验[15](简称K-S检验)对表1中数据进行定性和定量检验分析。

2.1.1 定性检验分析

对表1中数据取以10为底的对数，然后通过使用MATLAB软件中的Normplot函数分别对70、90、100K这3种应力水平下取对数后的数据进行正态性检验，其结果如图1。

从图1可看出：各应力水平下的数据均接近红线，取对数后的表1数据服从正态分布，这说明IGBT模块寿命服从对数正态分布。

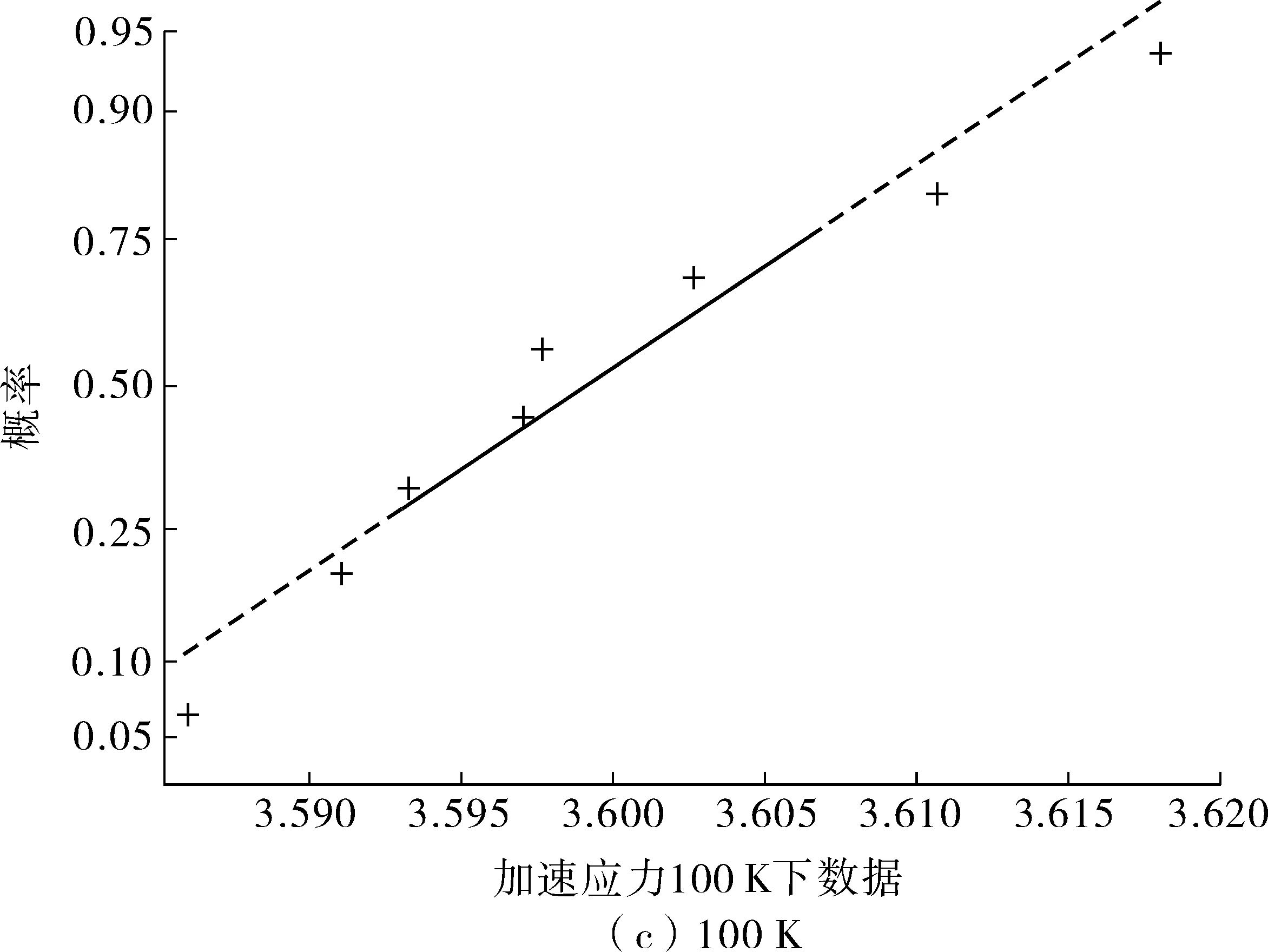
图1 3种应力水平下正态性检验Fig. 1 Normal test under three kinds of stress levels

2.1.2 定量检验分析

采用Weibull分布和对数正态分布对IGBT模块寿命进行分布假设检验，利用K-S检验来确定分布类型。K-S检验[16]为基于累积的分布函数，用来检验单一样本是不是服从某一预先假定的特定分布方法。将定量的正态检验问题转化为假设检验问题，即：

检验假设H0：F(x)=Fn(x)；

备选假设H1：F(x)≠Fn(x)；

其中：F(x)表示预先假设的特定分布；Fn(x)表示样本累积概率(频率)函数。

建立统计量D，如式(8)：

D=maxF(x)-Fn(x)

(8)

式中：n为样本容量。

单一样本容量n=8，由于样本容量较小，故取显著水平α=0.05，由单样本K-S检验统计可查得Dn,α=0.454 3。当D>Dn,α时，观测样本总体分布不服从某特定分布，即接受H1；反之，则为H0假设。表2为IGBT模块寿命的K-S检验结果。

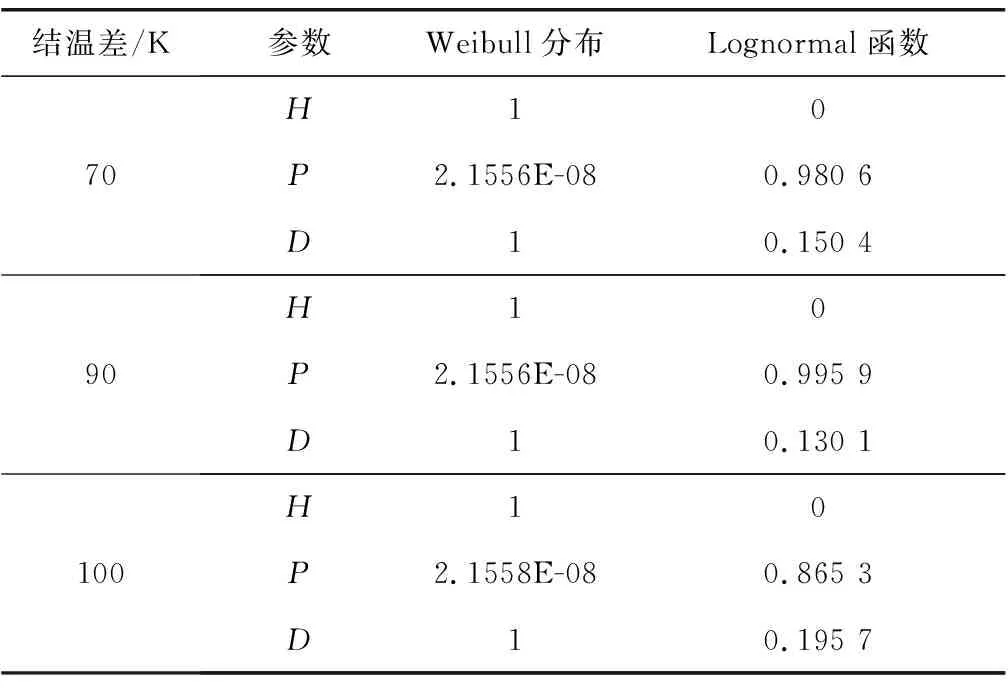
表2 IGBT模块寿命的K-S检验Table 2 K-S test of IGBT module lifetime

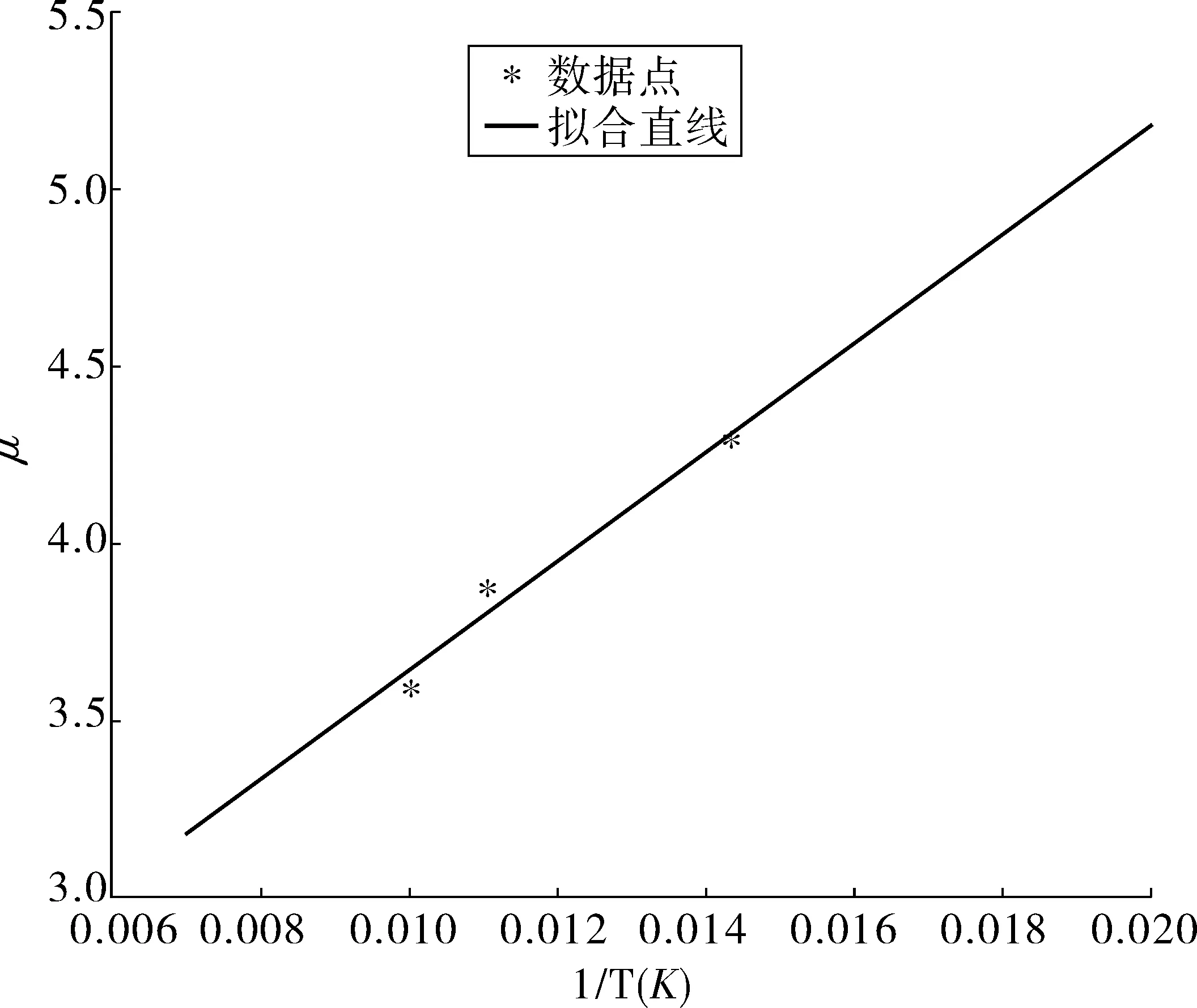
由表2可知：当威布尔分布K-S检验D>Dn,α，IGBT模块寿命分布不服从威布尔分布，接受H1假设；当对数正态分布K-S检验的D

2.2 加速寿命方程确定

结合式(7)可求得各加速应力下的对数正态的均值μ和标准差σ，如表3。

表3 各加速应力下的对数正态分布参数Table 3 Parameters of log-normal distribution underdifferent accelerated stress

各温差加速应力下的数据点(1/Ti,μi)，(i=1,2,3)如图2。

采用最小二乘法[17]拟合，求解得到式(3)中的加速参数a=2.106 4，b=153.803 6，则加速寿命方程如式(9)：

(9)

拟合的寿命特征曲线如图2。从图2中可看出：线性相关程度较好，说明IGBT模块加速模型满足阿伦尼斯方程。

图2 寿命特征Fig. 2 Life characteristics

2.3 基于ALTA软件的IGBT模块仿真

为再次验证IGBT模块寿命服从对数正态分布和分析其可靠性，笔者利用美国Reliasoft公司专为定量加速寿命测试数据分析而设计的ALTA软件对另一组IGBT模块加速寿命试验数据进行分析，具体数据如表4。

表4 IGBT模块加速寿命试验数据Table 4 Accelerated life test data of IGBT module

将试验数据输入ALTA，选择阿伦尼斯加速模型。由分布向导得知IGBT模块寿命分布函数服从对数正态分布。通过ALAT所提供的QCP可快速得到IGBT模块在正常工作情况下平均寿命为157 843 h。与计算对比，其误差为4.8%，小于5%，预测精度较高。除此之外，还可得到如BX%寿命、可靠寿命和条件可靠度等一些常用信息，如图3。

在ALTA中通过直观的概率图与结果面板，可快速、准确地获得最常见IGBT可靠性问题精确结果，其加速应力下的对数正态概率如图3(a)。由ALTA获取其相关参数之后，根据IGBT模块寿命分布符合对数正态分布，利用ReliaSoft Weibull++进行验证。由IGBT模块在ALTA 中得到的参数Log-Std和计算获得的参数Log-Mean值，并运用Weibull++Monte Carlo生成数据绘制该IGBT模块在正常应力下的对数正态概率，如图3(b)。

对比图3(a)、(b)，得知正常应力下对数正态概率保持一致。这亦说明了IGBT模块寿命数据服从对数正态分布。通过ALTA中生成的各种曲线图可直观分析IGBT模块的可靠性，为其复杂可靠性分析提供一种较为实用的方法。