基于改进PSO-BP网络的配电网故障选线与测距*

李升健，黄灿英，陈 艳

(1.国网江西省电力有限公司 电力科学研究院，南昌 330096；2.南昌大学 科学技术学院，南昌 330029)

随着我国经济的快速发展，配电网的规模和可靠性要求也在相应增加[1].然而据统计显示，线路故障导致了绝大多数电力系统的停电事故，其中，单相接地所导致的故障占到了总故障的50%以上[2]，因此，准确、快速地确定故障线路并计算其距离，对提高配电网的稳定性，保障生产生活的安全、稳定运行具有一定的意义.

配电系统的实际运行环境、接地方式和接地电弧等均将影响故障选线的效果[3-4].根据系统所采用的故障特征和结构，可将故障选线方式分为主动式[5]和被动式[6]两种.主动式选线根据人为注入的脉冲或交流信号的响应来判断故障线路；而被动式选线通过提取和分析馈线电压、电流等暂态与稳态特征来判断故障线路，包括稳态信号选线、暂态信号选线以及暂、稳态信号结合的方式选线.其中，稳态信号[7]选线主要包括电压、电流幅值、零序电流相比和五次谐波等；暂态信号选线[8-11]包括时频法和半波法等；暂、稳态信号结合的选线方式结合了暂态与稳态信号的特征，消除线路阻值和接地方式的影响，并使用SVM、粒子群算法等方式判断故障线路.

同理，根据系统的故障特征和线路结构可将配电网故障测距方式分为注入法[12]、暂稳态信号法[13]和人工智能测距法[14].虽然基于人工智能的方法取得了较好的选线和测距效果[15]，但各种智能算法仍存在陷入局部最优解的问题，其算法的鲁棒性和精确性可能无法满足要求.

针对上述问题，本文提出了一种基于改进粒子群优化神经网络(PSO-BP)的配电网故障选线与测距算法.首先引入混沌优化算法增强粒子群算法的收敛能力，并使用改进PSO-BP的参数得到改进PSO-BP模型；然后分别使用改进算法处理配电网故障选线和故障测距的问题，并使用Matlab软件进行仿真测试.

1 改进粒子群优化神经网络

1.1 基于混沌优化的粒子群算法

粒子群算法是由Eberhart和Kennedy根据现实生物群体活动开发出的智能优化算法，具有简单、收敛速度快和参数易设置的特点.然而，粒子群算法容易产生随机振荡，陷入局部最优解，并且学习因子和惯性权重的选择将制约算法的性能.因此，本文引入了混沌运动的概念，结合粒子群迭代与混沌映射的过程解决PSO算法早熟及收敛速度下降的问题.

混沌[16]即无规律可循，对初值敏感且具有随机性的运动过程，具有非周期性、长期不可预测性、遍历性和确定性等特点.混沌优化算法[17]在混沌运动的基础上，根据粒子自身的运动规律跳出局部最优，达到全局最优.混沌优化利用混沌变量映射到解空间，并使用混沌变量搜索求出最优解.混沌映射表达式为

xk+1=f(μ，xk)=μxk(1-xk)

(1)

式中，μ为控制参数，与变量x同时满足0≤x≤1≤μ≤4.式(1)表明，混沌优化过程不受外界的随机干扰，具体的混沌优化步骤如下：

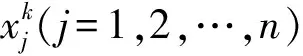
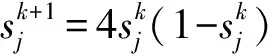
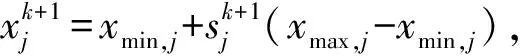
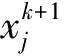
本文使用上述混沌优化算法增强粒子群算法的收敛能力，具体步骤为：

1) 初始化各粒子的位置和速度.

2) 计算各粒子的适应度值，并分别将各粒子的位置和适应度值存储在个体最优解pbest中，将所有粒子的pbest最优值存储在全局最优解gbest中.

3) 更新各粒子的位置和运动速度.

4) 计算各粒子的适应度值，并保留其中最优的40%粒子.

5) 进行混沌搜索操作，并更新gbest和pbest.

6) 若达到搜索停止条件，则输出结果；否则，跳转至步骤7).

7) 按照混沌优化方式收缩粒子搜索区域，即

(2)

式中，xg，j为全局最优解对应的粒子.

8) 在步骤7)收缩后的区域内随机长生60%的粒子，并跳转至步骤2).

详细的算法流程如图1所示.

1.2 基于改进粒子群的神经网络算法

传统的BP神经网络算法受网络参数和训练方式的影响，其收敛速度较慢且不能逼近其期望输出，因此，本部分使用上述混沌搜索改进的粒子群算法求解更优的BP神经网络参数.算法具体流程如下：

1) 使用经验公式确定各层的参数，即

(3)

式中，S1、R和S2分别为输出节点数、隐含层节点数和输入节点数.

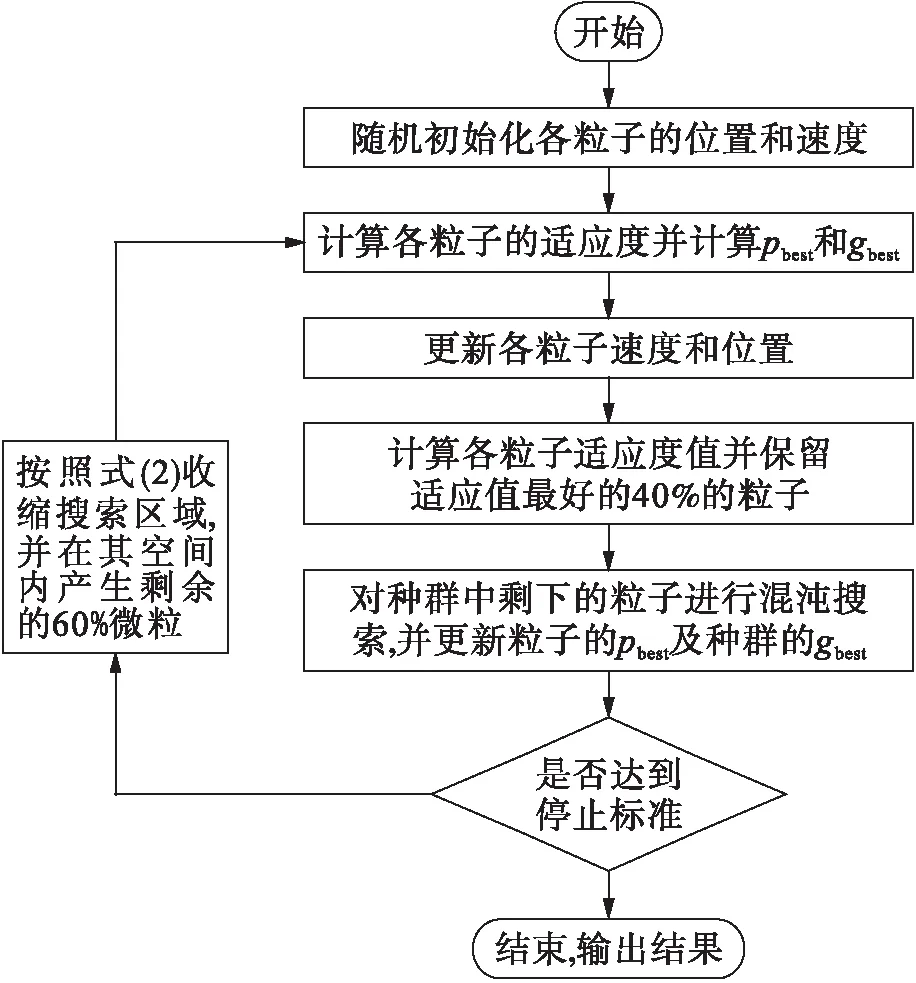
图1 基于混沌搜索的改进粒子群算法Fig.1 Improved PSO based on chaotic search

2) 初始化粒子群算法的参数.

3) 计算由网络输入和输出间的均方误差所确定的适应度函数，即

(4)

4) 使用改进的粒子群算法求解最优的神经网络权重参数，直至满足迭代停止条件.

2 配电网故障选线

使用上文提出的改进PSO-BP算法处理配电网故障选线的问题，其原理框图如图2所示.首先，获取配电网各条线路的零序电压和电流信号；然后，分别计算、提取电压和电流信号的暂态特征与稳态特征，并构造训练集、测试集；最后，使用训练集训练改进粒子群的神经网络算法模型，并使用测试集得到选线结果.

本文使用的暂态特征为暂态能量分量，稳态特征为五次谐波分量和零序有功分量，其计算方式如下：

1) 暂态特征分量.配电网单相接地时，在发生故障的瞬间，线路的电容和电感将产生充放电电流，并导致零序电流增大，因此，使用dB5小波包分解零序电流得到电流的暂态特征，其计算公式为

(5)

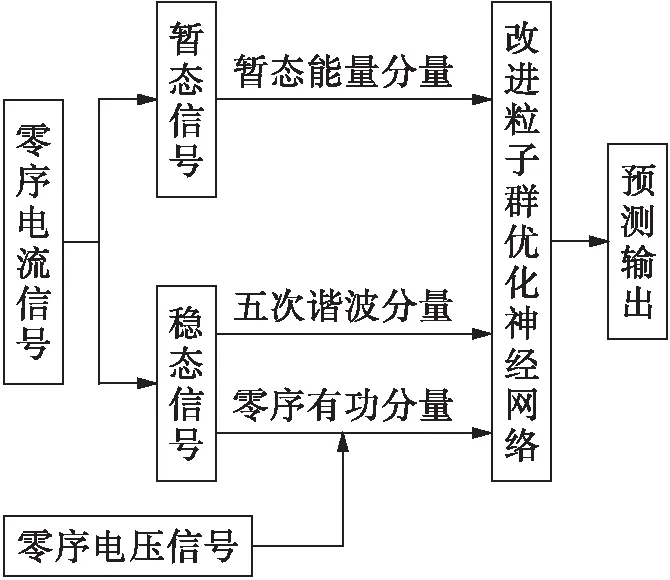
图2 故障选线系统框架Fig.2 Framework for fault line selection system

2) 五次谐波分量.配电网单相接地发生故障时的电流主要由基次谐波和基波构成，且其含量约为稳态电流的10%，因此，需提取谐波信号的幅值和作为稳态特征，幅值和计算公式为

(6)

式中，H(n)为谐波幅值.

3) 零序有功分量.配电网发生故障时，通常会导致零序有功功率的幅值偏大，零序有功分量特征提取公式为

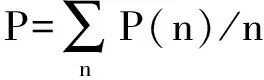
(7)

式中，P(n)为谐波有功功率的幅值.

3 配电网故障测距

使用改进粒子群神经网络算法解决配电网故障测距问题，其流程如图3所示.使用小波变换和傅里叶变换提取零序电压与电流的无功分量、基波分量以及小波能量分量构建特征向量，并训练改进粒子群的神经网络算法模型，再利用测试得到选线结果.

小波能量分量的计算表达式为

(8)

式中，S为频带系数.式(8)使用dB5小波包对故障信号进行4层分解，并分别采集16个子频的系数.配电网故障测距中使用的稳态特征为故障信号经小波变换和傅里叶变换后得到的零序基波分量与无功分量的幅值.

4 算例分析与仿真测试

本文利用如图4所示的包含5条线路的配电网故障模型进行仿真测试.该配电网各元件的频率为50 Hz，线路长度分别为12、14、16、18和20 km，接地电阻分别为Rg=100 Ω和RL=1 000 Ω.所使用的神经网络各层节点数为：输入层节点数为O，隐含层节点数为2O+1，输出层节点数为1.本文取O=3，即输入层节点数为3，隐含层节点数为7.

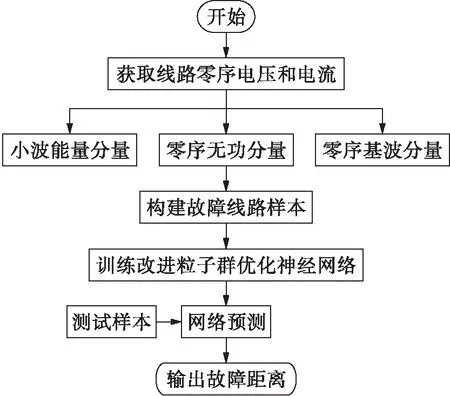
图3 故障测距流程Fig.3 Flow chart of fault location

图4 配电网故障仿真模型Fig.4 Fault simulation model for distribution network

本文分别提取了故障选线和测距模型的特征向量，其中，故障选线模型提取了不同故障初始角(0°、45°和90°)的特征向量；而故障测距模型提取了不同故障距离处的3维特征向量.分别对各组特征进行归一化处理以消除不同物理量之间的差别，并进行随机排序可得到如表1所示的样本数据.

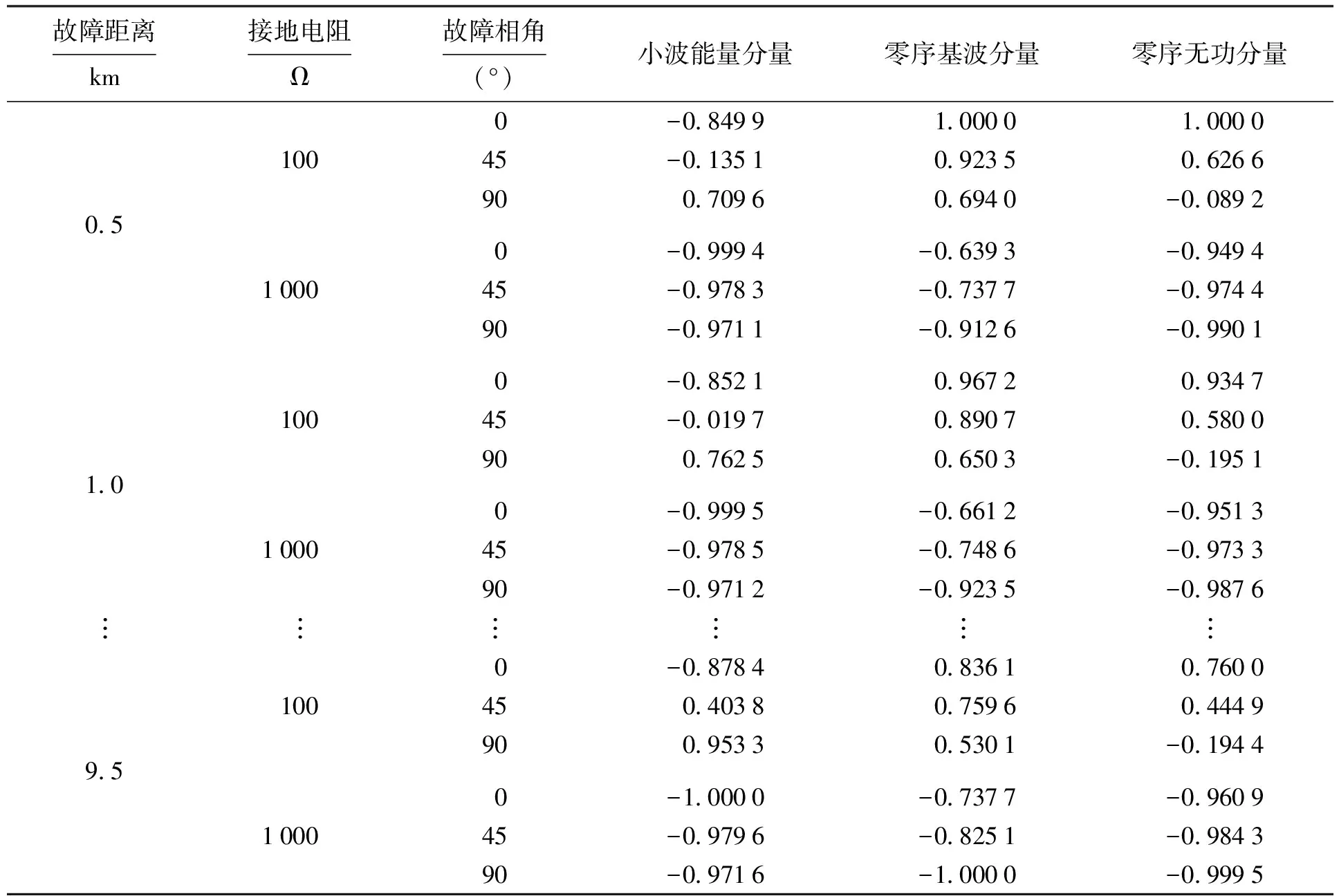
表1 故障样本Tab.1 Samples of fault

分别使用原BP算法、PSO-BP算法和改进PSO-BP算法进行选线比较，得到各测试样本的选线结果如表2所示.其中期望输出为线路的二进制表示，实际输出为每条线被选择的概率，概率越大表明越可能选择该条线路.从表2中可看出，所提出的算法具有更小的均方误差，预测的故障线路更逼近期望输出，故具有更优的故障选线性能.

表2 选线结果比较Tab.2 Comparison for results of line selection

使用原BP算法、PSO-BP算法和改进PSO-BP算法得到各测试样本的测距误差值如图5所示.从图5可以看出，相对于传统算法，改进粒子群优化的神经网络算法具有更精确的测距结果及更小的误差.由此表明，该算法受相位角和接地误差的影响更小，具有一定的鲁棒性.

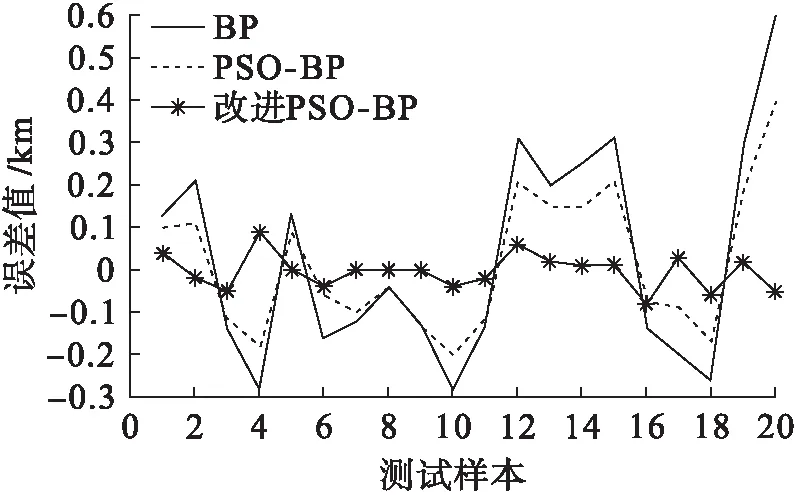
图5 测距结果误差比较Fig.5 Comparison in errors for results of location

5 结 论

人工智能算法在解决配电网故障选线和测距问题时容易陷入局部最优解，并存在难以满足精确性和鲁棒性要求的问题，因此，本文提出了一种改进PSO-BP的配电网故障选线与测距算法.算法先使用混沌优化算法增强粒子群算法的收敛能力，并用于训练神经网络参数，以提升神经网路的性能.实验仿真结果表明，将改进PSO-BP应用到配电网故障选线和故障测距中，能获得更精确的选线与测距结果.