金属材料割线模量峰值与其弹性极限的相关性*

康亚明，贾 延，牛 晟，罗玉财，陈静波

(1.北方民族大学 a.化学与化学工程学院，b.国家民委化工技术基础重点实验室，c.数学与信息科学学院，银川 750021；2.宁夏旭日众粒环保科技有限公司，银川 750200)

在制造业领域弹性极限是保证仪表用弹性合金正常工作的基本指标，准确测量材料的弹性极限是弹性元器件设计和材料合理使用的基础.在工程建设领域弹性极限也是保证构件或结构正常工作的基础.不同工况下的弹性极限以及屈服应力的理论分析与试验研究已经成为传统热点问题[1-3].在轴向拉伸或压缩试验中，随着应力的增加，材料内部自身结构会发生变化，随之出现了比例极限、弹性极限、屈服极限、强度极限等，而其中前3个强度特征值都可以表征金属发生微小塑性变形时所对应的抗力，很难进行严格区别，尤其是弹性极限和屈服极限，两者并无本质区别，只是对应的塑性变形大小略有差异[4]，这导致准确界定弹性极限只存在理论意义，换言之得到的数值仅为近似弹性极限.

1 割线模量与割线模量应变曲线

Ec=tanα=Δσ/Δε

(1)

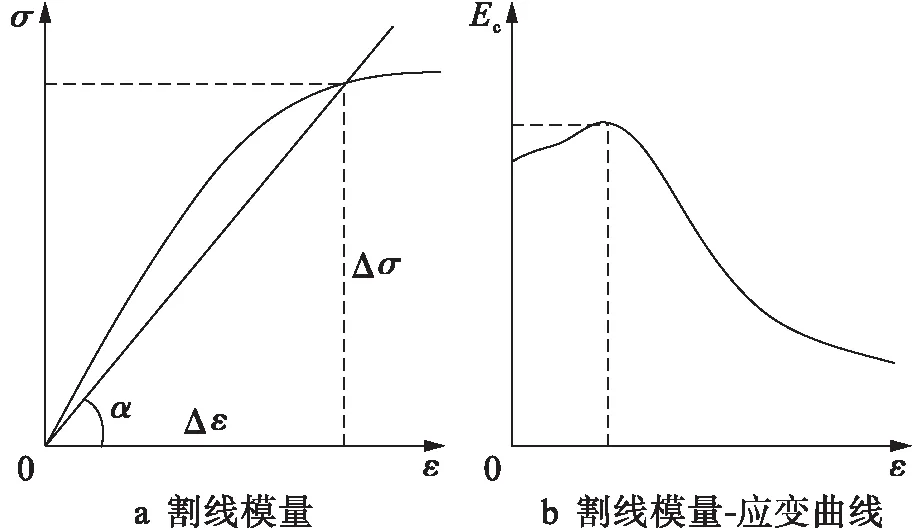
图1 割线模量及割线模量应变曲线Fig.1 Secant modulus and secant modulus-strain curve

2 高碳钢和低碳钢的单轴拉压试验

2.1 试件尺寸与试验要点

本文压缩试验采用直径为15 mm、长度为30 mm的圆柱试件，拉伸试验采用直径为10 mm、标距为100 mm的圆柱试件.采用位移控制模式进行加载，本文试验中加载速度为0.5 mm/min，在此加载速度下产生的应力速率符合GB/T 228.1-2010要求.试验温度为常温，符合GB/T 228.1-2010中试验温度为10～35 ℃的要求[11].

2.2 应力应变曲线和割线模量应变曲线

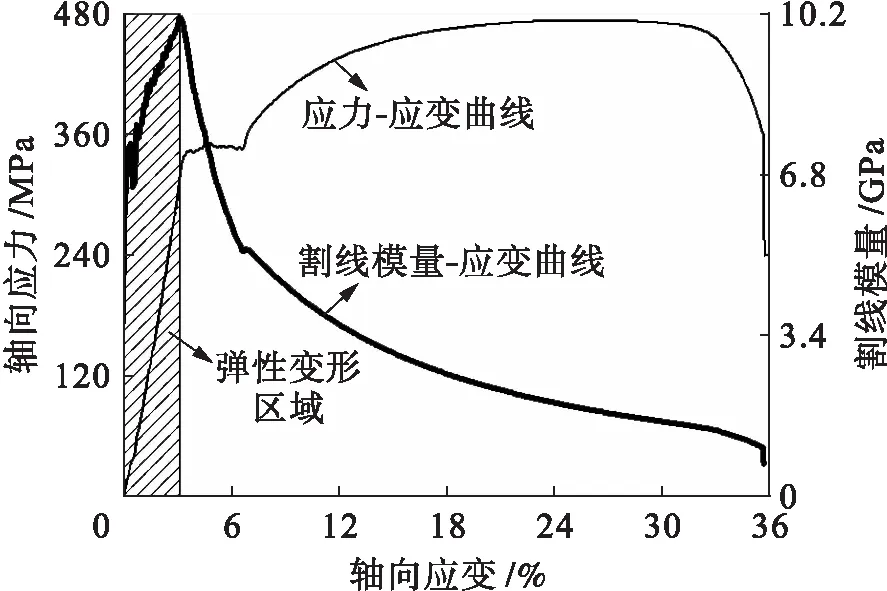
图2 低碳钢拉伸时的割线模量应变曲线Fig.2 Secant modulus-strain curve of low carbon steel subjected to tension

由图2～5可见，在应变全过程中割线模量一直在变化，在轴向拉伸或压缩时两种材料的割线模量具有如下规律：

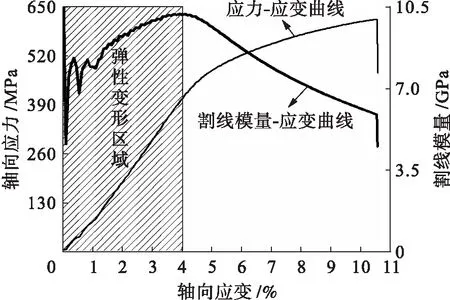
图3 高碳钢拉伸时的割线模量应变曲线Fig.3 Secant modulus-strain curve of high carbon steel subjected to tension

图4 低碳钢压缩时的割线模量应变曲线Fig.4 Secant modulus-strain curve of low carbon steel subjected to compression

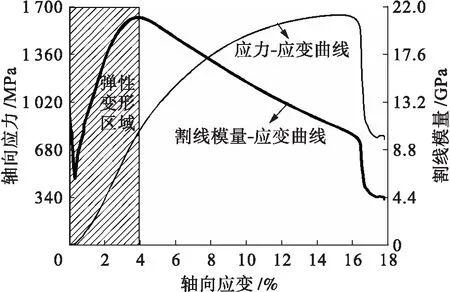
图5 高碳钢压缩时的割线模量应变曲线Fig.5 Secant modulus-strain curve of high carbon steel subjected to compression

1) 在应变全过程中割线模量先增大后减小，且存在明显峰值，且达到峰值后出现衰减现象；

2) 低碳钢延性特征明显，其弹性极限较为明显，不管是拉伸还是压缩状态，割线模量峰值均出现在弹性与塑性变形转换点附近；

3 割线模量峰值与弹性极限对应的佐证试验

为了证明割线模量峰值在弹性极限附近这一观点，开展了高碳钢在不同应变阶段的卸载试验.若在割线模量峰值前卸载，其残余变形接近于零，而在割线模量峰值后卸载，残余变形显著增大，则证明割线模量峰值与弹性极限确实具有对应关系，至少弹性极限就在割线模量峰值附近.割线模量峰值为判定弹性极限的重要参考.鉴于篇幅原因，本文只给出高碳钢的卸载试验曲线.

由图5可知，高碳钢单轴压缩时割线模量峰值出现在3.8%应变处，故本文围绕3.8%应变处进行多次独立卸载试验，即每个试件只做一次卸载试验，不能重复使用.具体卸载点为0.5%、1.5%、2.5%、3%、3.5%、4%、4.5%与5%应变处共8种情况，卸载曲线如图6所示.由图6可以获取不同应变处卸载后的残余变形.由图6可见，随着卸载位置的改变，卸载后的残余变形随卸载点应变的增大而增大.

为了直观地表示残余变形的变化，以卸载点处的应变为横坐标，卸载后的残余变形为纵坐标，绘制高碳钢在不同应变处卸载后的残余变形曲线，结果如图7所示.由图7可知，当卸载点处的应变超过3.5%后，残余变形迅速增加，而图5中割线模量峰值出现在3.8%应变处，可见两者较为接近.像钢材这种典型的均质材料，其弹塑性变形转换是一个连续过程，不存在绝对的明确界限，而当应力超过弹性极限后，塑性变形则变为一个逐步累加的过程.

张克球等[4]在对不同等级的热轧钢筋进行力学试验后发现，其屈服前的塑性应变如表1所示.由图6f可见，在4%应变处卸载后，高碳钢的残余变形为0.058 5%，该残余变形与表1中热轧钢筋在屈服前的塑性变形较为接近，表明热轧钢筋的弹性极限确实在4%附近，也间接证明了本文提出的利用割线模量峰值判定弹性极限的方法具有可操作性.

通过以上试验研究，本文从不同角度证明了割线模量峰值与弹性极限或上屈服强度之间的相对固定关系，但割线模量峰值是否受试验条件的影响还需要进一步考证.需要进行进一步分析的主要问题为：

1) 割线模量峰值可能受加载速度或边界条件等试验条件的影响；

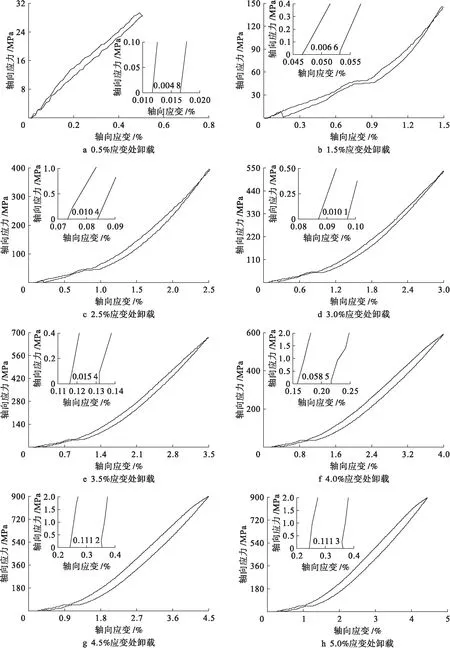
图6 高碳钢卸载后的应力应变曲线Fig.6 Stress-strain curve of high carbon steel after unloading

2) 割线模量峰值可能与试件的尺寸或形状有关，即可能存在尺寸或形状效应；

3) 割线模量峰值可能与试件所处的应力状态有关.

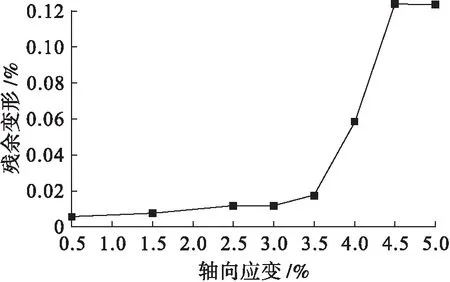
图7 高碳钢不同应变处卸载后的残余变形Fig.7 Residual deformation of high carbon steel after unloading at different strain

表1 热轧钢筋屈服前塑性应变Tab.1 Plastic strains of hot rolled bar before yield %

总之，以上因素既影响了割线模量峰值，也会影响弹性极限本身，因此，上述因素是否会影响到割线模量峰值与弹性极限的对应关系，需要进行进一步的试验研究.

4 结 论

3) 割线模量可能与加载速度、边界条件、应力状态等因素有关，也可能存在尺寸或形状效应，这些因素是否影响两者的对应关系还需进一步研究.