基于优化RVFLN模型的延迟焦化开工线H2S浓度预测
2019-01-15许霖风一偶国富金浩哲
许霖风一, 偶国富, 金浩哲
(浙江理工大学 流动腐蚀研究所, 浙江 杭州 310018)
随着原油资源趋紧,石油化工企业进口含硫和高硫劣质原油比例的逐年增加,延迟焦化成为当今炼油厂渣油尤其是劣质渣油处理的主要方式[1]。但是焦化装置腐蚀环境不断恶化,设备、管线的硫腐蚀已经成为影响焦化装置安稳、长周期运行的主要危害之一[2]。延迟焦化装置处理原料的硫含量过高,装置内部管线的湿H2S腐蚀和高温硫腐蚀已成腐蚀防控重点对象。刘宏波等[3]研究了单相流和多相流中的H2S电化学腐蚀与应力腐蚀开裂,得出了不同H2S浓度下N80钢的腐蚀规律;Sun等[4]用玻璃细胞实验分析了X65碳钢在高、低H2S浓度下形成的表面腐蚀产物,证明不同浓度的H2S会形成不同的金属表面腐蚀产物;王军等[5]针对我国高硫原油大型炼油厂设备的H2S腐蚀展开研究,分析了H2S腐蚀的主要影响因素并提出了相关的防护措施。
湿H2S与高温硫腐蚀的腐蚀速率都与管线内的H2S浓度密切相关,焦化装置处理原料硫浓度较大,运行过程中产生的H2S在管线死区堆积,与富含水气的管道发生化学反应,因此装置受到严重的湿H2S腐蚀危害。但是目前尚缺少测量封闭管道内部H2S浓度准确、实时的传感器;另外,石化企业现场工况运行数据库的大量历史数据尚未得到信息挖掘和有效利用。在工业环境中,广义线性模型如逻辑回归、偏最小二乘回归(PLSR)被广泛应用于过程变量的预测[6],因为此类模型输入直接,结构简单,可扩展性强,所以有快速的计算能力与特征保持功能。但是化工现场过程数据往往是高度非线性相关的,PLSR等线性模型无法处理变工况复杂环境下的高度非线性数据[7],而神经网络在处理非线性数据方面有一定的优势,如典型误差反传神经网络(BPNN),已被广泛应用于分类、预测[8]、回归等领域,然而BPNN算法权重更新较慢,且易陷入局部最小误差。
因此笔者采用一种单层前馈神经网络——随机权神经网络(RVFLN)作为基础算法进行优化,提出了小规范权重内随机权神经网络(SNRVFL)的数据驱动方法,并集成分析工业现场分布式控制系统(DCS)、实验室信息管理系统(LIMS)等数据库长期运行下的历史数据,建立关于H2S浓度的实时预测模型。最后在前期研究的基础上,通过分析延迟焦化系统的工艺流程,研究装置开工线管道的硫腐蚀机理,建立一种基于随机权神经网络算法的H2S浓度预测模型,模型的测试效果良好,适用于延迟焦化开工线的H2S浓度预测,为装置内压力管道的智能腐蚀防控与腐蚀风险评估提供数据基础。
1 延迟焦化装置工艺关联过程分析
1.1 延迟焦化装置流程
某炼油厂2#延迟焦化装置原料为减压渣油,其流程如图1所示。首先原料经过换热器(E-101A-F)换热后,进入原料油缓冲罐(D-101),然后由原料油泵(P-101A/B)抽出,经换热器(E-105A-F)换热后(301℃)与焦化分馏塔底循环油(360℃)混合(318℃)进入加热炉进料缓冲罐(D-102)。然后由加热炉进料泵(P-102A/B)抽出进入焦化加热炉(F-101A/B)并加热至500℃,再经过四通阀进入焦炭塔(C-101A-D,图中仅显示C-101A/B两装置)底部,然后通过2台焦炭塔进行生产。4台焦炭塔成对操作,一台运转24 h后,分别经过小吹气、大吹气、给水、溢流、生焦、清焦等工艺过程,将焦炭从塔底排除,焦炭塔塔顶的气流继续进入分馏塔完成循环。停工再生产时,原料通过四通阀从焦炭塔塔底和开工线同时进入塔内进行预热,其余工况下物料均从焦炭塔底进入。
开工线仅在停工生产时输入进料预热,其余工况下混杂着一定浓度H2S的气体均滞留在开工线管道顶部无法排除,故开工线顶部(图1中红框部分)是焦化装置腐蚀程度最严重的区域。停工检修时拍下的开工线内湿H2S腐蚀形貌图如图2所示。
1.2 湿硫化氢腐蚀机理研究
装置在给水、吹起、溢流、清焦等工艺过程中会产生大量水气,且开工线内部温度长期处于30~120℃之间,在此种低温、潮湿环境下,高浓度的H2S极易引起设备管线的低温湿H2S腐蚀,腐蚀反应总化学式为:
xFe+yH2S→FexSy+yH2
(1)

图1 延迟焦化装置工艺流程图Fig.1 Flow chart of the delayed coking plant1—Heat exchangers E-101A-F;2—Feed buffer tank D-101;3—Feed pumps P-101A/B;4—Heat exchangers E-105A-F;5—Furnace feed buffer tanks D-102;6—Furnace feed pumps P-102A/B;7—Furnaces F-101A/B;8—Coke drum C-101A;9—Coke drum C-102A;10—Fractionator T-101;11—Recycle oil pumps P-103A/B

图2 延迟焦化装置开工线内壁腐蚀照片Fig.2 Picture of corroded start-up pipeline inner wall of a delayed coking unit
电离过程:
Fe→Fe2++2e-, H2S→HS-+ H+
(2)
腐蚀反应式:
HS-+Fe2+→FeS↓+H+, 2H++2e-→H2
(3)
当液相介质呈现一定酸性时,FeS保护膜会被破坏,设备材料表面重新暴露易腐蚀环境中,促进了氢去极化腐蚀反应[9]:
Fe2++H2S→FeS↓+2H+
(4)
这些反应产生的氢离子容易渗入金属内部四处扩散,当遇到氢陷阱(如在晶界或相界上缺陷、位错、三轴拉伸应力区等)时,堆积增多的氢离子会重新结合生成氢气,引起陷阱处的高氢压力,使金属在内部产生细微裂纹,进一步加剧腐蚀。
根据以上分析,操作人员根据开工线内部温度以及H2S浓度来对设备进行腐蚀防控是可行且必要的,但由于湿H2S腐蚀机理复杂,焦化流程冗长且工况变化频繁,封闭管线内部难以测量,操作人员无法根据实时变化的H2S浓度采取相关防腐措施,因此建立开工线内H2S浓度的实时预测模型具有重要意义。
2 随机权神经网络算法介绍
2.1 影响因子选取及主成分分析降维
焦化装置开工线内H2S浓度受众多工业过程变量的影响,如果将装置所有相关的过程数据作为模型的输入,会造成大量数据信息的冗余,高维度的输入变量将会大大增加算法的计算量,影响数据的使用效率和运算速率。主成分分析法(PCA)对于处理高维非线性相关数据有较好的表现。因为实际工业相关数据中总是存在噪声扰动,且高维度的过程变量之间通常存在一定相关性,相关变量之间所反映的某一信息就会有所重叠。因此PCA通过正交变换将原先收集的所有变量,转化为一组线性不相关的变量,特征值大的相关成分被认为是有效的主要成分,小特征值的相关成分代表信息中的噪音,然后删除多余重复的变量(关系紧密的变量),建立尽可能少的新变量,从而将获得的低维主要成分来代替原始变量,达到过滤噪声、减小维数的目的[10-11]。PCA作为基础的数学分析方法,在此不再展开介绍。
而在回归领域中,皮尔逊相关系数(r)通常被采用,表示输入和输出之间的相关性。分析两者之间的关系时,筛选相应特征作为模型的输入,其公式见式(5)。
(5)

为了降低模型维度,减小计算量,提高运算速率,可采用主成分分析法对4组不同焦炭塔的H2S浓度进行降维,提取主特征;然后用皮尔逊相关系数筛选与输出相关性大的过程变量,作为模型的输入。笔者采取工业现场DCS、LIMS数据库中某一段时间内(大于延迟焦化装置的生产周期)的焦化装置实际生产数据,根据延迟焦化装置实际运行工况,计算了数据样本中各类数据特征与H2S浓度之间的皮尔逊相关系数,结果如表1所示。
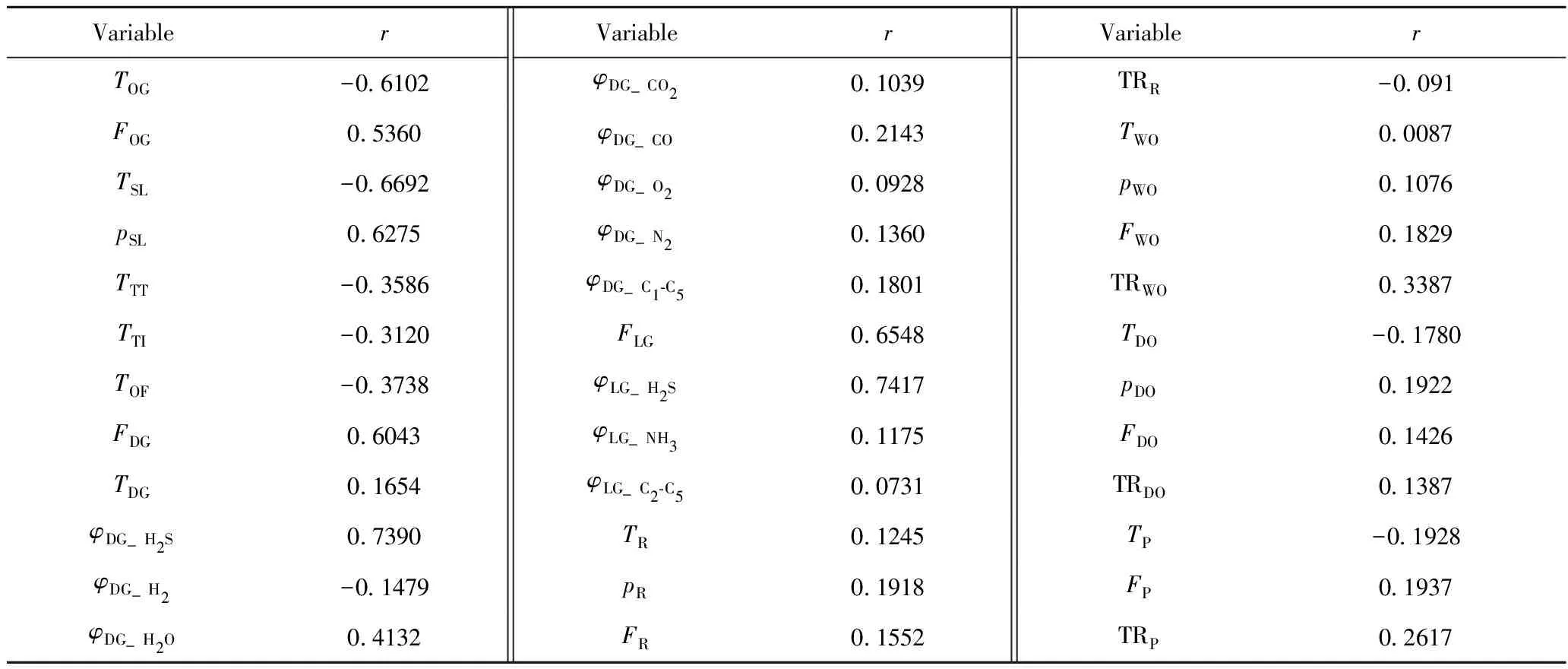
表1 各影响因子与H2S浓度间相关系数(r)分析Table 1 Correlation analysis between correlation coefficient(r) and H2S concentration
T—Temperature;p—Pressure;F—Flow;φ—Volume fraction;TR—Distillation range;OG—Oil gas line;SL—Start-up line;TT—Top of coke drum;TI—Tower inlet;OF—Overflow line;DG—Dry gas;LG—Liquefied gas;R—Residuum;WO—Wax oil;DO—Diesel oil;P—Petrol
由表1可知,开工线温度、开工线压力、干气H2S体积分数、干气流量、液化气H2S体积分数、液化气流量、油气线总管流量、油气线总管温度这8个因子的相关系数绝对值明显要大于其余影响因子,证明开工线内H2S浓度受此8种因素的影响最大,且开工线温度一项与H2S浓度的相关系数为负值,说明在低温情况下H2S浓度反而较高,H2S管道的腐蚀程度也随之上升,与案例实际腐蚀情况相符。
2.2 RVFLN算法结构简介
RVFLN是一种单层隐层前馈网络(SLFN),最早由Pao和Takefuji于1992年[12]在函数链接型神经网络(FLNN)的基础上[13]提出的,其性能已经在各种应用领域得到证实。与典型3层BP神经网络不同,RVFLN的输入层经过拓展后形成新的隐含层,和原始输入一起作为新的输入集进行模型训练[14]。M维输入X=[x1,x2,…,xM] 和L维输出Y=[y1,y2,…,yL]的RVFLN结构如图3所示。
图3中iM、hK、oL分别为输入层、隐含层、输出层各层节点的值,输入层原始输入变量X=[x1,x2,…,xM]经过附着随机权重后,得到第k个隐含层拓展节点的值为:
(6)
式(6)中,hk表示第k个隐含层拓展节点的输出值;wmk是连接第m个输入层节点到第k个隐含层节点的权重;bi,k是第k个隐含层节点的输入偏置;fk是第k个隐含层节点的非线性拓展函数,其一般使用sigmoid逻辑函数、三角多项式[15]以及切比雪夫多少项式[16]等,sigmoid逻辑函数如式(7)所示。
(7)
在随机权神经网络中,wmk、bi,k均在模型初始化时随机产生且固定不变,无须进行更新。Bartlett[17]和Huang等[18]指出,相较输入特征直接放入模型用于进行算法训练,给输入附着上[0,1]小规范内的权重会使算法有更好的泛化性能,本文中的wmk、bi,k均取[0,1]内的随机数。结合输入与隐含层节点的输出,则图3中输出层节点的值(yl)可以表示为:
l∈{1,2,…,L}
(8)
式(8)中,wml、wkl分别为输入层、隐含层到输出节点的权重系数;bi,l、bh,l为第l个输出节点的输入层、隐含层偏置;g为输出层节点激活函数,笔者采用sigmoid逻辑函数。由于输入层到隐含层的权重无需更新,将输入层和隐含层的节点均视为模型输入,式(8)可简写为:
(9)
因此,为了使算法达到预置误差要求,只需要更新输出层的连接权重wj以及输出节点的偏置bl即可,保证了模型的计算速率。
2.3 SNRVFL模型的建立
在经过PCA降维和相关性因子的选取后,建模的具体步骤如下:
(1)首先采用离差归一化对样本数据归一化:
(10)
式(10)中,S为原始样本集;Smax、Smin是样本S中每列特征数据最大值、最小值组成的矩阵;Sample表示归一化后的样本数据集。然后将样本随机地分成训练集Str、验证集Sva和测试集Ste,训练集用于模型训练,验证集用于网络隐含层节点数选取,最后测试集用于评估模型的性能。
(2)随机产生一组[0,1]之间的拓展权重,连接输入层节点与隐含层节点;然后将隐含层视为拓展节点,与原始输入一起构成最终的输入矩阵I。
(3)初始化输出层权重W在[-1,1]区间内。
(11)
与实际输出间的误差记为E,
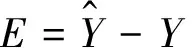
(12)
(5)用误差反传的方法更新权重W,l是模型的学习率,取l=0.7:
(13)
式(13)中,Wold表示更新前的权重矩阵;Wnew表示更新后新得到的权重矩阵。
(6)判断更新后的权重是否达到误差要求,如果达到,记下当前权重,模型建立完成;如果未达到,则继续进行第(4)步至第(5)步,直到模型满足要求。
3 SNRVFL模型预测H2S浓度性能评估
3.1 实例数据采集预处理
由于4台焦化塔成对操作流程一致,此章节仅以C-101A焦化塔为考察对象作为示范,建立塔C-101A内的H2S浓度实时在线预测模型。结合2.1节中的影响因子相关系数分析,选取了8个相关性较大的影响因子作为模型的输入变量,分别为C-101A开工线温度、C-101A开工线压力、出口干气H2S体积分数、出口干气摩尔流量、出口液化气H2S体积分数、出口液化气摩尔流量、油气线总管流量、油气线总管温度;输出变量为焦化塔C-101A开工线的H2S浓度。其中输入数据的过程变量均可从现场DCS和LIMS数据库中采集得到,模型输出变量H2S浓度数据来自课题组前期开发的测量软件,部分历史数据如图4所示。
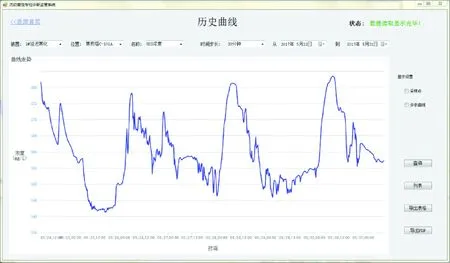
图4 现场测量软件焦化塔管线内H2S质量浓度变化曲线图Fig.4 Real historical curve of H2S mass concentration in the coking drum pipeline by field measurement software
为了保持输入输出的频率一致,以输出变量H2S为最低采样频率,从现场数据库中获取了一段时间内同时刻的4000组输入、输出作为数据样本,然后利用数据样本根据2.3节中所给的步骤建立预测模型。采取均方根误差(RMSE)衡量算法模型,对于H2S浓度的预测精度进行计算,见式(14)。
(14)
3.2 SNRVFL结构确定
当隐含层激活函数选为sigmoid函数时,为了确定随机权神经网络最优的隐含层节点数,需要用训练集和验证集对算法不同隐含层节点下的拟合程度进行模拟,计算各个隐含节点时算法的最终误差,模型的误差随隐含层节点数的变化关系如图5所示。
从图5可知,当隐含层节点小于24时,验证集误差和测试集误差均随隐含层节点数增加而减小,在此区域算法属于欠拟合状态。而在隐含层节点大于24之后,虽然训练集的误差依然缓慢变小,但验证集的误差开始逐渐增大,模型趋于过拟合状态,因而确定模型隐含层节点数为24时可取得较好的建模效果,可避免节点过少时的拟合程度欠佳与隐含节点数过多导致的过拟合且降低工作效率,最终建立8-24-1的随机权神经网络模型。

图5 SNRVFL模型H2S浓度训练集误差与验证集误差随隐含层节点数的变化关系Fig.5 Variation relationship between errors of the H2S concentration train dataset, validation dataset and numbers of hidden nodes with SNRVFL model
3.3 SNRVFL模型与其他模型效果比较
为了验证所得SNRVFL算法模型在预测焦化装置开工线H2S浓度方面的快速性与准确性,将建模效果与偏最小二乘回归(PLSR)、支持向量回归(SVR)、BP神经网络(BPNN)进行比较。对比PLSR、SVR、BPNN 3种常用算法模型,测试集的H2S浓度分布计算效果模拟分布图和残差值如图6所示。由图6可知,显然SNVRFL模型的H2S浓度预测曲线拟合度最高,PLSR因为处理非线性数据能力较差,预测曲线波动幅度最大,不太适合于H2S浓度的准确预测。对比4种算法的残差值,SNVRFL前65个测点的残差在[-1.5,1.5]之间,均在0误差标准线附近,说明该种算法的预测值最接近运行工况实际值,其预测性能最佳。

图6 H2S浓度测试集在PLSR、BPNN、SVR、SNRVFL 4种算法下的模拟分布图和残差图(前65个测试点)Fig.6 Analog distribution and residuals for H2S mass concentration testing dataset from PLSR, BPNN, SVR and SNRVFL algorithms (first 65 test points)(a) Analog distribution; (b) Residuals
从算法结构上说,SNRVFL与BPNN均属于需要更新权重的神经网络,由于SNRVFL输入层到隐含层的权重是小范围内([-1,1])随机确定的,因而只需要更新链接输出层与其上一层之间的权重即可,迭代速率明显快于典型的3层BPNN,其比较结果如图7所示。
最后为了证明算法在精度与速率方面的优势并非偶然性,随机打乱初始样本重新分配训练集与测试集(交叉验证),用SNRVFL、PLSR、SVR、BPNN 4种算法模型分别模拟10次,计算各自均方根值(RMSE)与运行时间,结果见表2。

图7 BPNN与SNRVFL迭代速率比较(隐含层节点数均为24) Fig.7 Comparison of iteration speed between BPNN and SNRVFL(24 hidden layer nodes)

OrderRMSECalculation time/msPLSRSVRBPNNSNRVFLPLSRSVRBPNNSNRVFL111.3757.3758.1077.1341391360413629.7687.5966.9637.05914876592130310.3247.4557.8386.89116924625127410.7897.7418.3247.17711967613284512.0408.1948.2657.35113893587134610.1977.4307.7296.72914901682141711.0067.1627.9147.58214928601135811.9147.8788.4867.23115913579133910.7627.4299.0597.109129576101621012.3077.9387.8027.17813864599149Average11.0487.6208.0497.14414914609153
综合图6~7与表2可以看出,SNRVFL较其他3种算法有更好的预测能力和泛化性能,在计算精度上,SNRVFL10次预测的均方根误差平均值为7.1441,是4种算法模型中最小的,说明SNRVFL对该工况下的H2S浓度预测最精准;而且SNRVFL模型的运算速率也明显要快于SVR和BPNN,说明SNRVFL模型处理非线性数据的能力很好且有快速实时的预测速率。因而SNRVFL模型的准确快速与全面性使其可用于焦化系统开工线内H2S浓度的在线实时预测。
4 结 论
针对炼油企业延迟焦化装置管线硫腐蚀严重的问题展开研究,分析确定延迟焦化装置开工线内腐蚀原因为低温湿H2S腐蚀,基于SNRVFL优化算法建立了延迟焦化装置开工线内H2S浓度的预测模型,首先对现场DCS、LIMS数据库采集的各种数据特征进行降维预处理,对比影响因子相关系数大小,结合湿H2S腐蚀机理,提取了影响开工线内H2S浓度的主要因素。然后为提高算法的非线性能力与泛化性能,对特征变量附着小范围内随机权重并引入非线性函数拓展模型的输入特征,用误差反传算法对输出权重进行更新。计算结果表明,与其他算法比较,SNRVFL误差收敛速率快,运算速率良好(仅次于PLS),预测精度高且具有较好的泛化性能。SNRVFL算法模型效率、准确且全面,故认为此方法可作为延迟焦化装置开工线内H2S浓度的智能预测模型。
