盾构隧道管片横向变形对接头抗弯刚度的影响

□文/张茜珍 陈 翰 郑力铭

存在大量接头是盾构隧道的一大特点，管片接头部位既是隧道抗变形相对薄弱的部位，又是隧道结构病害高发的部位，接头刚度的大小对于管片环整体力学性能的发挥起着至关重要的作用。

在盾构隧道管片结构计算模型中，通常采用kθ、kn、kv分别表示管片接头的抗弯、抗压及抗剪刚度；其中最能体现接头性能的参数是kθ，定义为接头处产生单位转角对应的弯矩[1]。目前研究[2～4]主要针对接头附近区域或相邻管片，与管片环的真实受力状况存在差别，更无法真实体现正负弯矩区域接头性能。本文引入不考虑弹性衬垫的管片接头力学模型，采用三维实体有限元方法模拟管片结构真实变形及受力状态，通过“经典条带法”反算结构弯矩，基于M-θ关系曲线求得kθ，最后分析盾构隧道横向变形对接头刚度的影响。

1 有限元模拟方法

由于平面计算模型无法考虑螺栓类型、接头处接触状态等问题，采用三维实体有限元方法进行数值模拟，以使计算结果更接近实际情况。

以上海市轨道交通通缝拼装管片为例，管片环宽取1.2 m、外径6.2 m、内径5.5 m、厚0.35 m，每环管片由1块拱底块（TD）、2块标准块（TB）、2块邻接块（TL）、1块封顶块（TF）组成。见图1。

图1 通缝拼装管片分块

实际工程采用C55混凝土，5.8级螺栓。混凝土抗压强度设计值25.3 MPa、抗压强度标准值35.5 MPa、弹性模量34.5 GPa，泊松比0.2；螺栓直径30 mm，屈服强度400 MPa，极限强度500 MPa，弹性模量210 GPa，泊松比0.27。

结合研究对象的特点和实际情况，取单环管片，忽略防水密封垫及沟槽的影响，不考虑管片及螺栓生产及拼装过程中的误差，采用ANSYS中的Rush模型实现应力-应变曲线的输入，将Rush模型单轴受压应力-应变曲线改造成三折线模型，从而避免数值模拟不收敛的问题[5]，见图2。

采用理想弹塑性本构关系描述螺栓受拉的应力-应变关系，管片实体及螺栓均采用实体单元进行模拟，三折线本构模型中各阶段弹性模量及相关转点应变见表1。

采用映射网格划分方法将单元划分为六面体，见图3。

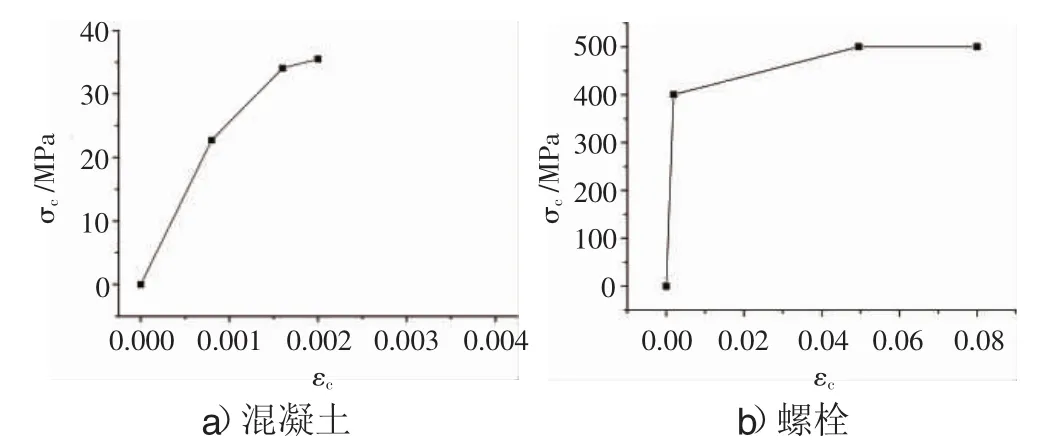
图2 基于Rush模型的三折线本构模型

表1 本构模型参数

图3 管片结构及螺栓有限元模型

既有资料显示，上海软粘土地层中修建隧道时，隧道拱顶土压力实测值随时间而增加，最后十分接近上覆土重[6～7]。因此在计算中忽略两侧地层对隧道上覆土柱产生的反向摩擦力及土拱效应，隧道拱顶土压力等于上覆土重计算采用的荷载模式见图4。

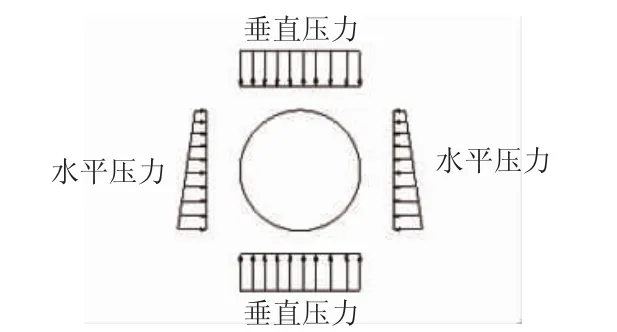
图4 管片结构荷载模式

2 盾构隧道管片接头抗弯刚度理论模型

2.1 力学计算模型

盾构隧道管片结构最显著的特征就是存在大量接头，接头处的刚度不可能与管片本身相同。接头既非刚接，也不是完全铰接[1]，它是一个能够承担部分弯矩的弹性铰；而弯矩能够通过接头传递多少，与接头刚度成正比；因此管片接头是设计中必须考虑的重要因素，也是结构计算的重要内容。目前常用的盾构隧道管片接头力学计算模型主要有：不考虑弹性衬垫的接头模型、考虑弹性衬垫的接头模型等。

对于不考虑弹性衬垫的接头模型，使用较为广泛的是小泉淳和村上博智提出的接头计算模型，见图5。

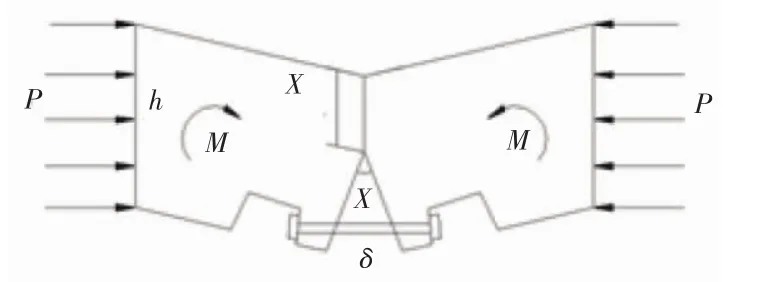
图5 不考虑弹性衬垫的接头模型

管片结构在弯矩M和均布面力P的作用下，产生弯曲和变形，接头面上部受压，下部受拉脱开，受压区高度x可根据实际计算结果确定。管片接头变形后，由受压区混凝土和受拉区螺栓共同承受外部荷载。

可由此计算M-θ关系曲线的接头转角θ。当θ较小时，近似满足

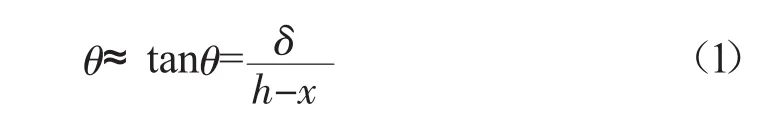
式中：θ为接头转角，×10-3rad；δ为接头张开量，mm；h为管片厚度，mm；x为受压区高度，mm。

经典条带法[8]是在不考虑弹性衬垫接头模型的基础上，将管片接头处截面划分为若干条带，在上述平截面假定前提下，通过力和力矩的平衡求解接头面的轴力N和弯矩M。由于接头处有混凝土和螺栓两种材料，接头面一部分受压、另一部分受拉张开且受压区压应力分布不均匀，这使得接头力学模型的截面受力非常复杂。这种情况下，使用条带法可以将截面分层，分别定义每层的材料性质和应力状态。见图6。

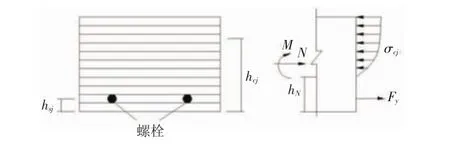
图6 条带算法

由此计算M-θ关系曲线的弯矩M。根据截面处的平衡条件可得

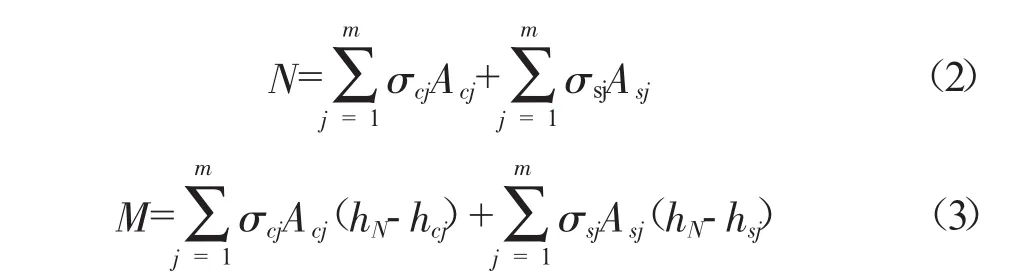
式中：σcj为第j层混凝土截面分割带应力，kN；Acj为第j层混凝土截面分割带面积，mm2；σsj为第j个螺栓的应力，kN；Asj为第 j个螺栓的面积，mm2；hN为截面底部与弯矩参考轴的距离，mm；hcj为截面底部与第j层混凝土截面分割带的重心的距离，mm；hsj为截面底部与第j个螺栓的距离，mm。

截面处的压应力为正，拉应力为负。使用“条带算法”分析不考虑弹性衬垫的接头模型，主要任务就是求解上述两个方程。截面处的材料状态及应力状态都是非线性变化的，如果所取每个条带的宽度都足够小，则可以认为每个条带的材料状态及应力状态是一个定值，这样将提高计算效率。

2.2 理论模型

董新平[9]认为，结构所承受的轴力是决定接头抗弯刚度及接头极限承载力的控制性因素。朱伟等[10]分析了轴力对接头抗弯刚度的影响，轴力越大，对应的接头抗弯刚度越大。在接头构造既定的情况下，土体的侧压力系数对结构轴力影响较大，因此侧压力系数对接头抗弯刚度影响较大。分别对土体侧压力系数为0.6、0.65、0.7三种情况下的接头刚度进行分析。

将不同侧压力系数下的正负弯矩区域M、θ数据整理，以此分析kθ。见图7和图8。

图7 正弯矩区域M-θ关系曲线

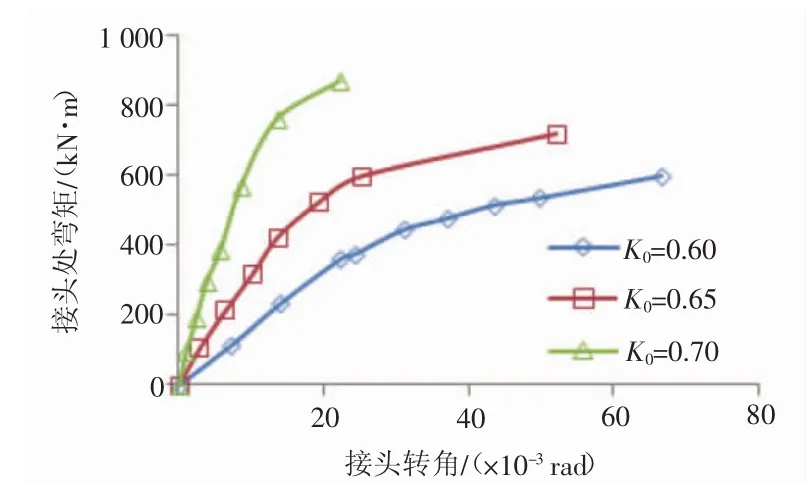
图8 负弯矩区域M-θ关系曲线

采用多段线法对M和θ数据进行拟合并以M-θ关系曲线的切线斜率作为接头抗弯刚度kθ，建立基于多段线法的接头抗弯刚度的双直线模型，见图9。

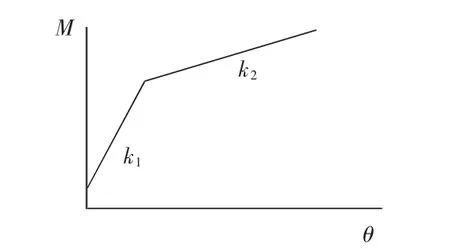
图9 接头抗弯刚度的双直线模型

M-θ关系曲线中接头抗弯刚度的双直线模型可表述为

式中：M为接头弯矩，kN·m；θ为接头转角，×10-3rad；a1、a2为拟合系数，kN·m；k1k2为拟合系数，MN·m/rad。

对θ求导，可得接头抗弯刚度的双直线模型

正弯矩区域M-θ关系曲线的切线斜率k1、k2分别表示第一、二阶段的接头抗弯刚度，不同侧压力系数情况下的相关拟合系数见表2，负弯矩区域M-θ关系曲线的相关拟合系数见表3。

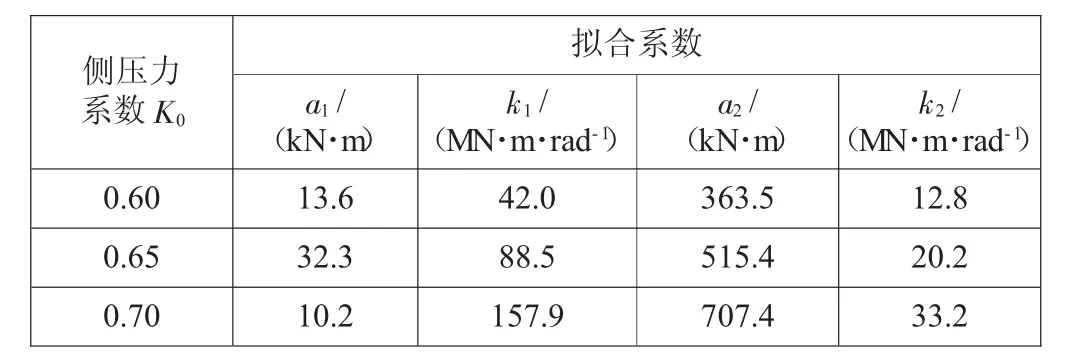
表2 正弯矩区域M-θ关系曲线数据拟合结果

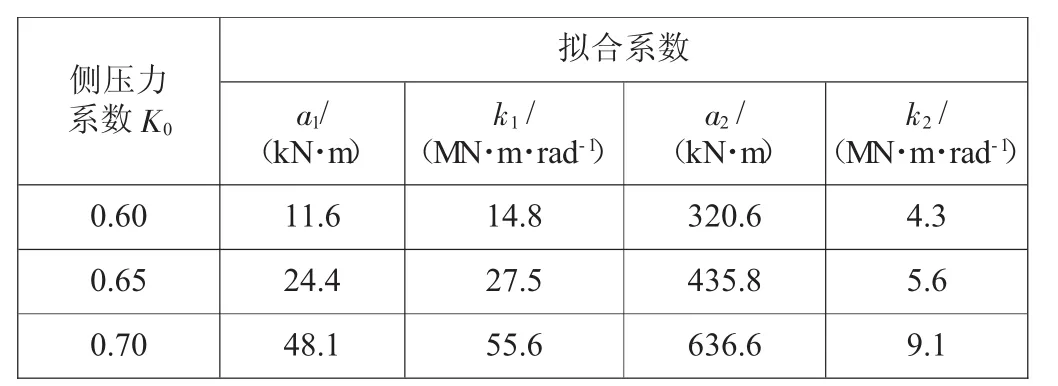
表3 负弯矩区域M-θ关系曲线数据拟合结果

不同侧压力系数条件下，第二阶段的接头抗弯刚度k2均远小于第一阶段的k1。以侧压力系数0.6为例，正弯矩区域 k1为 42.0 MN·m/rad、k2为 12.8 MN·m/rad，负弯矩区域 k1为 14.8 MN·m/rad、k2为 4.3MN·m/rad，第二阶段的接头抗弯刚度k2仅为k1的1/3左右。

正负弯矩区域的k1、k2均随侧压力系数的增大而增大。以正弯矩区域的k1为例，随侧压力系数的增大，k1分别为 42.0、88.5、157.9 MN·m/rad，可见侧压力系数对接头刚度影响较大。

kθ的取值范围通常为 10～100 MN·m/rad[11]，本文正负弯矩区域接头抗弯刚度双直线模型的计算结果基本处于常用取值范围内。定义正弯矩区域的接头抗弯刚度为，负弯矩区域的接头抗弯刚度为，根据 K.M.Lee等[12]接头加载试验，对盾构隧道通缝拼装的管片结构接头抗弯刚度取值提出如下建议

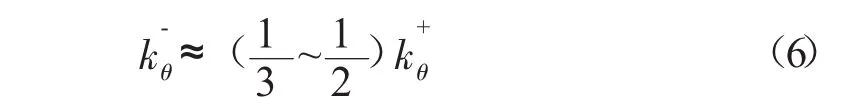
正负弯矩区域的接头抗弯刚度值与K.M.Lee的试验规律基本一致，可以说明通过M-θ关系曲线得到的接头抗弯刚度双直线模型是合理的。

3 盾构隧道横向变形对接头刚度的影响

随着管片结构横向变形的发展，横向整体刚度和接头刚度都会相应发生变化。结构横向变形量与整体刚度及正负弯矩区域的接头刚度均具有一定的对应关系，盾构隧道结构横向变形在一定程度上体现了结构性能的发展规律。

盾构隧道结构横向变形主要指标为水平直径变化量ΔD，接头刚度则主要考虑接头抗弯刚度kθ或接头抗弯刚度比λ，分析ΔD的变化对λ的影响。

对于类型、尺寸既定的管片结构，随着结构横向变形的不断发展，接缝张开量增大，螺栓、接头处混凝土应力增大，接头刚度随之下降。土体侧压力系数对正负弯矩区域的接头刚度均有较大影响，考虑侧压力系数为0.6、0.65、0.7三种情况下，ΔD的变化对λ的影响。

三次多项式可以较好反映出变化趋势，二者存在如下函数关系

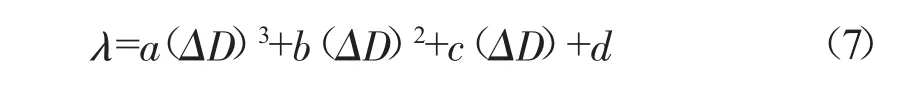
对侧压力系数为0.6、0.65、0.7时的λ-ΔD关系曲线数据进行拟合，见表4-表6。

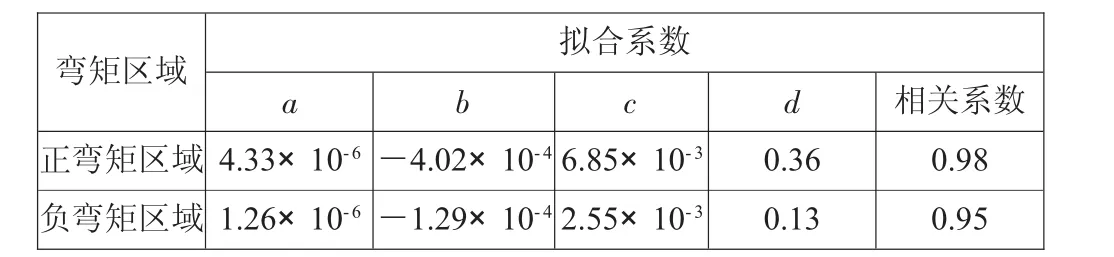
表4 侧压力系数0.6时λ-ΔD关系曲线数据拟合结果

表5 侧压力系数0.65时λ-ΔD关系曲线数据拟合结果

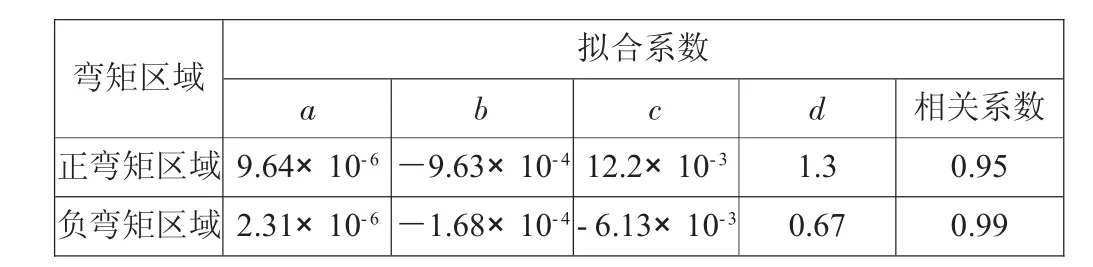
表6 侧压力系数0.7时λ-ΔD关系曲线数据拟合结果

4 主要研究成果

1）在不考虑弹性衬垫的接头力学模型基础上，建立管片接头抗弯刚度的双直线模型，分别得到正负弯矩区域的接头抗弯刚度拟合结果，负弯矩区域的接头抗弯刚度约为正弯矩区域的1/3～1/2。

2）不同侧压力系数下，正负弯矩区域的接头抗弯刚度比λ均随管片直径变化量ΔD的增大呈非线性减小趋势。