Z字形飞机建模与半实物仿真研究

刘东辉 王金豪 孙晓云 王晓 徐静静

摘 要：为了提高无人机飞行品质，研究无人机控制的半实物仿真应用，形成一套通用的无人机飞行控制律设计与半实物仿真方法，针对气动特性较为复杂的Z字形飞机进行了研究。Z字形飞机机翼可向机身方向折叠，便于存放和运输。根据Z字形飞机外形参数，求得气动数据，并在此基础上利用小扰动线性化原理建立纵向线性模型，通过加入干扰脉冲方式研究模型纵向静稳定性，选取各环节传递函数，建立俯仰控制回路，调整PID参数，设计纵向控制律，分别使用Simulink和半实物仿真器进行仿真。仿真结果表明，无人机具有较好的静稳定性，PID控制参数选择合理，系统超调量较小，调节时间较短，可以提升无人机飞行品质，半实物仿真可以更真实、直观地反映无人机姿态，所用建模与仿真方法可应用到其他固定翼无人机，具有一定的通用性。

关键词：控制系统仿真技术;无人机;数学模型;控制律;半实物仿真

中图分类号：V249.1   文献标志码：A   doi：10.7535/hbkd.2019yx06009

Abstract：In order to improve the flight quality of UAV， study the hardware-in-the-loop simulation application of UAV control， and form a set of universal UAV flight control law design and hardware-in-the-loop simulation method， the Z-shaped aircraft with complex aerodynamic characteristics is studied. The Z-shaped aircraft can be folded in the direction of the fuselage for easy storage and transportation. According to the shape parameters of Z-shaped aircraft， the aerodynamic data are obtained. On this basis， the longitudinal linear model is established by using the principle of small disturbance linearization. The longitudinal static stability of the model is studied by adding disturbance pulses. The transfer function of each link is selected， the pitch control loop is established， the PID parameters are adjusted， the longitudinal control law is designed， and simulation is conducted by using Simulink and hardware-in-the-loop simulator. The simulation results show that UAV has good static stability， reasonable selection of PID control parameters， small system overshoot and short adjustment time， which can improve the flight quality of UAV. Hardware-in-the-loop simulation can more truly and intuitively reflect the advantages of UAV attitude. The modeling and simulation methods have certain universality and can be applied to other fixed-wing UAVs.

Keywords：control system simulation technology; UAV; mathematical model; control law; hardware-in-the-loop simulation

無人机是依靠无线电设备或自身程序控制的不载人飞行器[1]，具有成本低、损耗低、可重复使用和机动性高的特点，广泛应用于现代生活和军事的多种领域。

飞行控制系统是无人机的核心部分。无人机姿态、速度、高度等的变化都依赖于飞行控制系统。此外，无人机必须能够适应飞行过程中的各种不确定性，例如：复杂的空气环境，自身状态的变化，战斗任务的调整等[2]。飞行控制系统的品质决定了无人机的性能。因此，构建无人机数学模型并设计其飞行控制律具有十分现实与深远的意义。对于无人机控制仿真，传统的软件仿真方式在某些方面具有局限性，如模拟飞行环境不够真实、观察实验现象不够直观等，而半实物仿真方式通过将部分无人机部件加入仿真系统中，使得仿真结果更加真实可信。

本研究针对Z字形飞机，利用飞行器设计与分析工具DATCOM求得气动数据，使用小扰动线性化原理建立线性模型，采用PID控制方法设计纵向控制律，最后使用半实物仿真系统验证其实用性。

1 无人机数学模型构建

1.1 气动数据的求取

Z-shaped aircraftZ字形飞机机体结构形似字母“Z”，其机翼分别位于机身顶端和尾端，并且可向机身方向折叠，折叠后所占用的空间大大减小，有便于存放和大批量运输的特点。Z字形飞机俯仰控制舵位于机翼尾沿，形状为矩形。方向控制舵位于机身尾部，呈扇形垂直分布。整机质量3.0 kg，翼展1.3 m，机翼弦长0.15 m，翼型Clark Y，机翼面积0.144 m2，机身长度0.8 m，机身宽度0.15 m。由于其具有较为特别的结构，因此，气动特性也相对复杂，对控制律要求较高，有一定的研究价值。Z字形飞机外形如图1所示。

根据无人机的外形参数，利用DATCOM可求得所需气动数据。DATCOM是由美国空军力学实验室编写的气动数据估算程序，集合了大量经验数据，可以通过飞机外形参数计算气动数据[3-6]。将无人机的外形参数按照其编程格式要求写入输入文件中，运行DATCOM程序后将自动输出含有各项气动数据的输出文件。所选无人机的主要气动数据见表1。

2 无人机控制律设计

2.1 稳定性判定

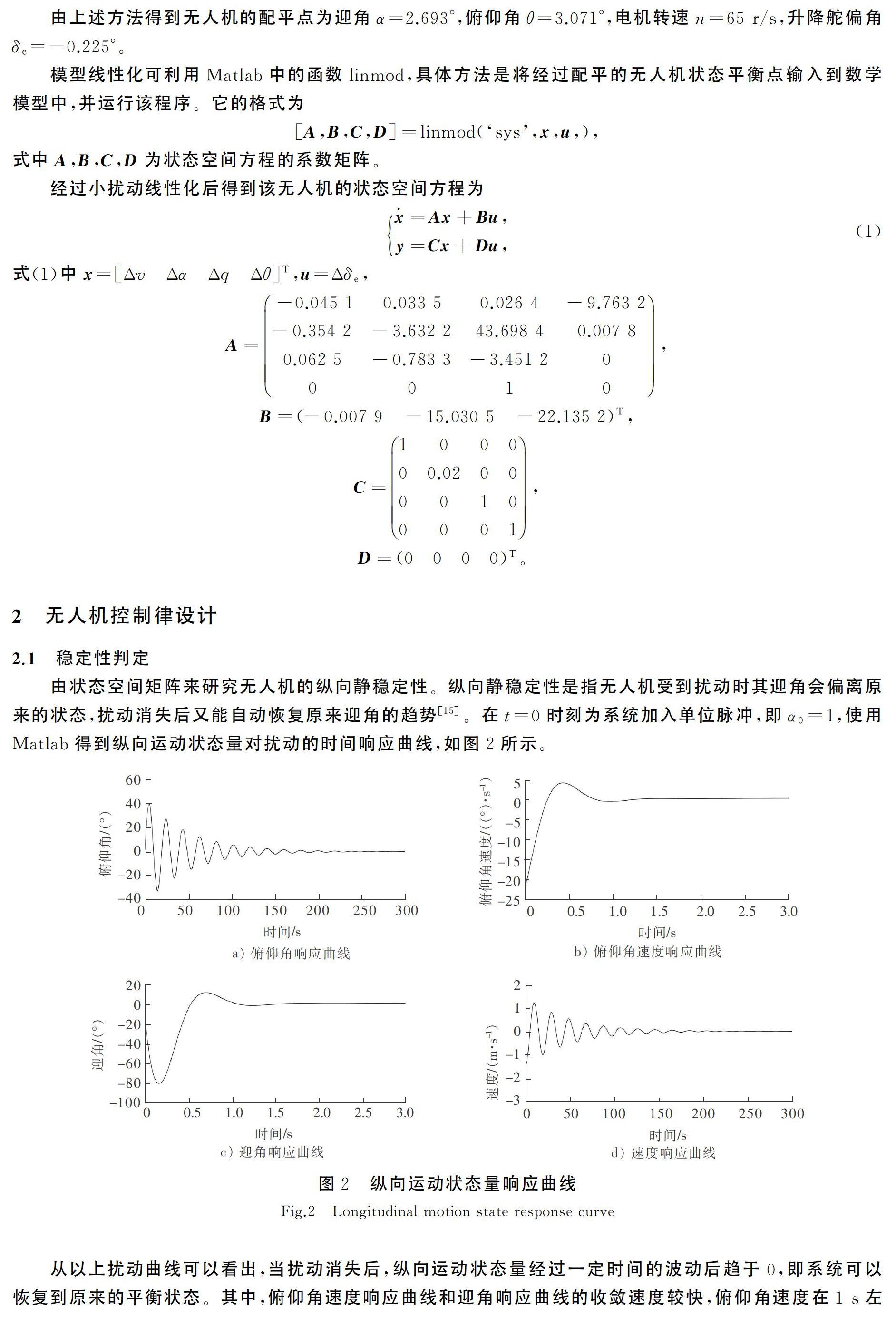
由状态空间矩阵来研究无人机的纵向静稳定性。纵向静稳定性是指无人机受到扰动时其迎角会偏离原来的状态，扰动消失后又能自动恢复原来迎角的趋势[15]。在t=0时刻为系统加入单位脉冲，即α0=1，使用Matlab得到纵向运动状态量对扰动的时间响应曲线，如图2所示。

从以上扰动曲线可以看出，当扰动消失后，纵向运动状态量经过一定时间的波动后趋于0，即系统可以恢复到原来的平衡状态。其中，俯仰角速度响应曲线和迎角响应曲线的收敛速度较快，俯仰角速度在1 s左右达到平衡状态，迎角在1.5 s左右达到平衡状态，因此俯仰角速度和迎角为短周期状态量。俯仰角响应曲线和速度响应曲线的收敛速度较慢，在250 s左右达到平衡状态，为长周期状态量。

为了验证在不同飞行条件下无人机的静稳定性，选取迎角分别为3°，6°和9°来观察迎角响应曲线，见图3。由图3可知，增大迎角后状态量的波动虽有所增加，但并不明显，且可以在短时间内达到稳定状态。这说明该无人机具有静稳定性，验证了模型的正确性，可以用该模型设计控制律。

2.2 俯仰角控制回路设计

由状态空间方程可以求出升降舵到俯仰角速度的传递函数为q（s）δe（s）=-22.135 2s3-69.624 9s2-3.393 1ss4+7.128 5s3+47.094 1s2+2.661 5s+4.925 4 。  为了改善无人机的性能，可以在俯仰角控制回路中增加阻尼回路[16-18]。为了将俯仰角速度中的稳态分量滤掉，需要向内回路增加洗出网络[19]，最终俯仰角控制回路的结构图如图4所示。

由无人机特点将舵机假设为一个一阶环节，传递函数为-10/（s+10），而洗出网络的传递函数设为4s/（4s+1）[20]，最终的俯仰角控制回路的Simulink仿真图如图5所示。

输入单位阶跃信号，PID控制器的参数选为KP=25，KI=32，KD=0，仿真结果如图6所示。由图6可知，系统调节时间较短，且能良好地跟随输入信号，动态性能较好，可以满足设计要求。

3 半实物仿真研究

半实物仿真是指在仿真实验系统的仿真回路中接入部分实物的实时仿真[21]。本文使用北京灵思创奇公司的Links-Box-02仿真器进行仿真，该仿真器可外接遥控器、飞控板等无人机重要设备，也可通过无线信号连接三轴转台观察无人机实时姿态。具体来说，将无人机数学模型加载到仿真器，通过Simulink把以上得到的PID控制算法转换为程序下载到飞控板，便可利用仿真器模拟无人机在大气中的飞行姿态，并且可由遥控器在线控制，相应的姿态也可由三轴转台动态显示出来。半实物仿真系统如图7所示。

为了观察其可控性，将无人机模型和控制算法分别下载到半实物仿真器和飞控板中，并且将无人机的核心部件飞控板置于三轴转台的平台上。因飞控板内部有陀螺仪，所以转台的运动可以带动陀螺仪变化从而反映无人机在空中的姿态。由无人机实物（飞控板和遥控器）以及半实物仿真设备（仿真器和三轴转台）組成半实物仿真系统，如图8所示。

连接遥控器后，当未给任何输入信号（遥控器信号）时该无人机的姿态趋于平稳，当给抬升信号时无人机俯仰角上升（曲线上升），给下落信号时无人机俯仰角下落（曲线下降），停止输入信号其姿态又趋于平稳，仿真曲线如图9所示。

无人机的姿态变化通过三轴转台实时显示出来，其运动迅速且准确，更加直观地反映控制律的可靠性。三轴转台瞬时姿态如图10所示。

4 结 语

以Z字形飞机作为建模对象，使用DATCOM程序求取气动数据，利用小扰动线性化方法建立数学模型，并在此基础上研究无人机静稳定性，设计俯仰控制律，进行Simulink和半实物仿真。实验表明：该无人机具有静稳定性，所设计的控制律能满足控制要求;半实物仿真系统可外接无人机飞控板和遥控器，仿真效果更加真实可靠;三轴转台模拟无人机动作更便于观察，对无人机控制律设计与调试有较大帮助。所用建模与仿真方法可推广到其他型号无人机的控制系统，具有一定的通用性。

目前系统调节时间仍有改进空间，未来将对比使用多种控制算法以实现最优系统性能。此外，还将研究无人机自主起飞与降落等部分的半实物仿真，实现无人机飞行过程的全仿真。

参考文献/References：

[1] 冯军红，俆开俊，林娜. 民用无人机姿态稳定与航迹跟踪控制策略研究[J].西北工业大学学报，2018，36（2）：382-387.

FENG Junhong， XU Kaijun， LIN Na. Attitude stabilization and trajectory tracking control strategy for civil UAV[J]. Journal of Northwestern Polytechnical University，2018，36（2）：382-387.

[2] 张琳，龚喜盈，庞俊锋. 轮式起降无人机滑跑起飞阶段动力学仿真研究[J].航空工程进展， 2018，9（3）：375-381.

ZHANG Lin， GONG Xiying， PANG Junfeng. Dynamics simulation research on tricycle landing gear UAV during taxiing and take-off phase[J].Advances in Aeronautical Science and Engineering， 2018，9（3）：375-381.

[3]  GAVRILETS V，FRAZZOLI E，METTLER B，et al.Aggressive maneuvering of small autonomous helicopters：A human-centered approach[J]. International Journal of Robotics Research，2001，20（10）：795-807.

[4] 王鹏，周洲.飞翼无人机着陆滑跑建模和控制仿真研究[J].系统仿真学报，2011，23（1）：118-122.

WANG Peng， ZHOU Zhou. Study of modeling and control simulation for flying-wing UAV in ground motion during landing [J]. Journal of System Simulation， 2011，23（1）：118-122.

[5] 王程坤，李秀娟.轮式无人机地面滑跑模型的建立[J].电光与控制，2017，24（2）：89-94.

WANG Chengkun， LI Xiujuan. Establishment of taxiing model for a wheeled UAV[J]. Electronics Optics & Control， 2017，24（2）：89-94.

[6] 段镇，高九州，贾宏光，等.无人机滑跑线性化建模与增益调节纠偏控制[J].光学精密工程，2014，22（6）：1507-1516.

DUAN Zhen， GAO Jiuzhou， JIA Hongguang， et al. Linearized modeling and gain scheduling control for UAV taxiing [J]. Optics and Precision Engineering， 2014， 22（6）：1507-1516.

[7] 付国强，王立鹏，魏雅川，等.无人机全包线变增益调参控制律设计[J].计算机测量与控制，2019，27（4）：72-76.

FU Guoqiang，WANG Lipeng，WEI Yachuan，et al. Variable gain schedule control law design of UAV within full envelope[J]. Computer Measurement & Control，2019，27（4）：72-76.

[8] 华艺欣， 曹良秋. 一种评价无人机纵向飞行品质的简化分析方法[J].飞机设计，2018，38（5）：38-41.

HUA Yixin，CAO Liangqiu. A simplified method for evaluating UAV longitudinal flying qualities[J]. Aircraft Design，2018，38（5）：38-41.

[9] 董守田，杨利红，康成吉，等. 固定翼无人机姿态控制及仿真[J]. 东北农业大学学报，2015，46（9）：87-92.

DONG Shoutian， YANG Lihong， KANG Chengji， et al. Fixed wing UAV attitude control and simulation[J]. Journal of Northeast Agricultural University， 2015， 46（9）： 87-92.

[10] 鄭涛，高正红，孔祥俊.无人机系统的仿真建模研究[J].飞行力学，2012，40（3）：30-34.

ZHENG Tao， GAO Zhenghong， KONG Xiangjun. Research on simulation and modeling for unmanned aerial vehicle system[J]. Flight Dynamics， 2012，40（3）：30-34.

[11] 刘斌，贺剑，张琳.小型无人机动力装置建模与仿真研究[J].飞行力学，2010，30（5）：20-25.

LIU Bin， HE Jian， ZHANG Lin. Modeling and simulation on propulsion system of minitype UAV[J]. Flight Dynamics， 2010，30（5）：20-25.

[12]  SHTESSEL Y，BUFFINGTON J，BANDA S.Multiple time scale flight control using re-configurable sliding modes[J].Journal of Guidance Control & Dynamics，1999，22（6）：4196-4201.

[13] ZHOU K， DOYLE J C， GLOVER K. Robust and Optimal Control[M].[S.l.]：[s.n.]，1995.

[14] 杨新，王小虎，申功章.飞机六自由度模型及仿真研究[J].系统仿真学报，2000，25（5）：20-24.

YANG Xin， WANG Xiaohu， SHEN Gongzhang，et al. Modeling and simulation research of six-degree-of-freedom fighter[J]. Journal of System Simulation， 2000，25（5）：20-24.

[15] 王伟，张晶涛，柴天佑.PID参数先进整定方法综述[J].自动化学报，2000，26（3）：347-355.

WANG Wei， ZHANG Jingtao， CHAI Tianyou. A survey of advanced PID parameter tuning methods[J]. Acta Automatica Sinica， 2000，26（3）：347-355.

[16] 胡彬杨.无人机飞行控制方法研究与设计[D].成都：电子科技大学，2018.

HU Binyang. Research and Design of Flight Control Method for Unmanned Aerial Vehicles[D]. Chengdu： University of Electronic Science and Technology of China， 2018.

[17] 虞曉霞.无人机飞行姿态稳定控制技术研究[D].长春：长春理工大学，2018.

YU Xiaoxia. Research on Stability Control Technology of UAV Flight Attitude[D]. Changchun： Changchun University of Science and Technology， 2018.

[18] 陈伟，冯高鹏，拜云山.小型变体无人机动力学建模及配平分析[J].计算机技术与发展， 2017，27（2）： 125-129.

CHEN Wei， FENG Gaopeng， BAI Yunshan. Dynamics modeling and trimming analysis for small morphing UAV[J]. Computer Techno-logy and Development， 2017，27（2）： 125-129.

[19] OBRADOVIC B，SUBBARAO K.Modeling of flight dynamics of morphing-wing aircraft[J].Journal of Aircraft， 2011，48（2）： 391-402.

[20]  SEIGLER T M， NEAL D A， BAE J S， et al.Modeling and flight control of large-scale morphing aircraft[J].Journal of Aircraft，2007，44（4）： 1077-1087.

[21]  毛瑞燕，高国伟，徐万芝.航姿参考系统中磁航向传感器误差标定与补偿[J].传感器世界，2017，23（5）：33-37.

MAO Ruiyan， GAO Guowei， XU Wanzhi. Error calibration and compensation of magnetic heading sensor in AHRS[J]. Sensor World， 2017， 23（5）： 33-37.