基于信息位与校验位分离的RS码盲识别
2019-01-14杨俊安梁宗伟
龙 浪,杨俊安,刘 辉,梁宗伟
(1.国防科技大学电子对抗学院,安徽 合肥 230037;2.安徽省电子制约技术重点实验室,安徽 合肥 230037)
0 引言
RS(Reed Solomon,RS)码是一类纠错性能优异的多进制BCH(Bose Chaudhuri Hocquenghem)码,它具有编码结构简单,纠正随机错误和突发错误能力强的特点,被广泛应用于无线通信、深空通信、军事通信等各个领域中[1]。因此,研究RS码的盲识别方法有重要意义。
现有的文献表明,国内外已有大量学者对RS码盲识别算法展开研究。文献[2]利用衡量谱分量概率分布差异性的欧几里德距离测度来完成对RS码本原多项式和生成多项式的识别,但对RS码其他编码参数识别未做详细研究。文献[3]通过求取矩阵的差值函数来识别码长及符号数,并利用熵函数差值来完成对本原多项式的识别,但该方法计算量较大,抗误码性能较差,且只适用于本原RS码,不能识别出缩短RS码。文献[4]通过码重分布识别码长,并利用二元假设识别本原多项式和生成多项式,减少了计算量,但同样不适用于缩短RS码。文献[5]通过伽罗华域(Galois Field,GF)的高斯约当消元法识别码长,并利用伽罗华域傅里叶变换(Galois Field Fourier Transform,GFFT)识别本原多项式和生成多项式,该方法虽然可完成对RS码和缩短RS码的识别,但计算量较大,抗误码性能不佳。综上,已有的算法没有较好的权衡算法的计算量和抗误码性能,且识别的参数不够全面,均未对RS码的信息位长度这一参数进行识别,并且针对RS缩短码的识别研究相对较少。针对以上存在的不足,本文提出一种基于信息位与校验位分离的盲识别算法。
1 RS码识别基础
1.1 RS码的定义
定义1[6]:GF(q)(q≠2,通常q=2m)上,码长n=q-1的本原BCH码称为本原RS码。
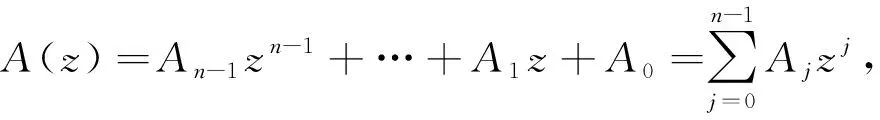
在实际应用中q一般取2m,所以主要对GF(2m)上的RS码进行识别研究。
1.2 RS码的性质
RS码是线性分组码的一种重要子类,所以RS码具有线性分组码的性质。
性质1[8]:设V是由GF(2m)上的k×n阶生成矩阵G所生成的RS码,则V的向量表示(mn,mk)是GF(2)上的线性分组码。
若将GF(2m)上的(n,k)RS码映射为GF(2)上的线性分组码,其中n为RS码码长,k为RS码信息位长度,m为符号数,则GF(2)上的等价线性分组码码长mn=m(2m-1),等价信息位长为mk,其中m≥2。
性质2[5]:RS码的码字信息位与校验位线性相关。
性质3[9]:多项式a(x)以αj为根的充要条件是其谱多项式A(z)的系数满足:Aj=a(αj)=0
性质4[9]:对任一距离为δ的RS码字进行伽罗华域上的离散傅里叶变换,则A(z)中至少有δ-1个连零。
对于缩短RS码[10],它是原(n,k)本原RS码删除前i位信息位为0的码字后所构造的新码,由于仍可构成一个(k-i)维的线性子空间,所以能得到一个(n-i,k-i)(1≤i≤k)的缩短RS码,其码长n≠2m-1,其他参数均与原RS码相同,因此,对缩短RS码的识别方法与原RS码一致。
2 RS码盲识别实现
在实际数据传输中,(n,k)RS码通常是以二进制码流(mn,mk)传输的[11],当截获到RS码序列后,根据RS码的线性特性,对接收序列构建等效二进制码的分析矩阵,通过信息位与校验位分离法,识别出等价码长mn,等价信息位长mk,从而获得码率k/n,再通过伽罗华域的离散傅里叶变换求出RS码的符号数m,本原多项式p(x)及生成多项式g(x),最后通过计算可获得码长n,信息位长k。
2.1 基于信息位与校验位分离的盲识别算法
本文通过信息位与校验位分离法来完成对RS码等价码长mn及等价信息位长度mk的识别,即通过等价二进制码流中0,1概率方差的不同来区分信息位及校验位,从而确定mn及mk。例如,在实际应用中,(7,3)RS码通常是以等价(21,9)二进制码来进行传输的,其中m=3。令等价二进制码中信息位1的概率为a(0 (1) 如校验位c10是信息位m1和m2异或相加所得,则校验位c10为1的概率如式(2): P(c10=1)=P(m1⊕m2=1)=P(m1=1)× (2) 同理,校验位c10为0的概率如式(3): P(c10=0)=P(m1⊕m2=0)=P(m1=1)× (3) 为了更好地说明信息与校验位分离法,计算校验位c10所在列(校验列)的1和0概率的概率方差d1与信息位所在列(信息列)的概率方差d2,其中均值μ=(a+b)/2=0.5,定义两者的差值为d3,通过比较可得,信息列概率方差大于奇偶校验列概率方差,由此可以区分信息位和奇偶校验位。 d1=(a-0.5)2+(b-0.5)2 (4) d2=[(a2+b2)-0.5]2+(2ab-0.5)2 (5) d3=d1-d2=(a-0.5)2+(b-0.5)2- (6) 故定义分析矩阵的每列0、1的概率方差d(i)如式(7),其中col为分析矩阵的列数。 d(i)=variance(P(0),P(1));1≤i≤col (7) 与校验位所在列的概率方差相比,消息列的概率方差将会较大,计算所有col列概率方差的方差d如式(8): d=variance(d(1),d(2),…,d(col)) (8) 当分析矩阵中码字对齐时,即信息位与校验位恰好分离,此时,各列之间的概率方差的差异最大,总的概率方差达到一个最大值。当分析矩阵中码字未对齐时,列中的元素既有信息位也有校验位,则此时各列之间概率方差的差异不明显,总的概率方差相对较小。 因此,通过观察分析矩阵取不同列数值下的总概率方差d,当d为最大值时,此时的分析矩阵中码字对齐,且码长估计准确,由此可以得到正确的等价码长mn及等价信息位长mk。 2.1.1等价码长识别 假设码长为5的截获RS码序列以不同的估计码长按行放入分析矩阵中,其中令A,B,C为信息位,D,E为校验位,形成的矩阵模型如图1所示。 图1 三种排列情况Fig.1 Three cases of arrangement of bitstream 现在,可能有三种排列的情况: 图1(a)表示当码字对齐,且每行对应于实际的等价码长大小为5时,A,B,C,D,E各自单独成列,信息位与校验位分离,所以最终的方差d会出现最高峰。 图1(b)显示当每行大小为4,即不等于实际的等价码长大小时,A,B,C,D,E不能单独成列,每列既包含信息位A,B,C,又有校验位D,E,信息位不能与奇偶校验位分开,所以最终的方差d不会出现最高峰。 图1(c)示出了当码字未时对齐,A,B,C,D,E不能单独成列,每列既包含信息位A,B,C,又有校验位D,E,信息位不能与奇偶校验位分开,所以最终的方差d不会出现最高峰。 在构建分析矩阵后,计算每列的0、1概率方差及所有列概率方差的方差d,当且仅当码字对齐,且每行对应于实际的等价码长大小时,方差d最大,完成对等价码长mn的识别。 2.1.2等价信息位长识别 与校验列的概率方差相比,消息列的概率方差将会很大,因此可以区分信息位和奇偶校验位。 当码字对齐且等价码长估计正确时,按正确的码长构建分析矩阵,计算每列的0、1概率方差d(i)。与校验列相比,等价信息位所在列的概率方差大于校验列的概率方差,由此可区分出校验列与信息列。为了更好的进行区分,取分析矩阵所有列概率方差的均值为门限值Vth。 (9) 当概率方差d(i)超过Vth时,判断该列为信息列,反之,则为校验列,由此,可识别出等价信息位的长度mk,通过计算可以得到RS码码率k/n。 当等价码长估计正确且对齐后,选择不同的估计符号数m0,由于RS码的性能随码长的增加而降低,实际一般使用中短码,符号数m0取3~8,并遍历m0次本原多项式pr0,对截获序列按估计出的正确等价码长mn进行分组,并对其作GF(2m0)上的离散傅里叶变换。当多组码字经GF(2m)上的傅里叶变换后具有相同的连零位置且个数相同时,则正确识别出符号数m及本原多项式pr,最后通过计算可以得到RS码的码长n,信息位长度k。其中符号数m及其本原多项式如表1所示。 表1 m值及其对应的本原多项式十进制表示 设α表示GF(2m)的本原元,那么{1,α,α2,…,α2m-2}是GF(2m)上的2m-1个不同的非零元素。最小码距为d=2t+1(t=(n-k)/2)的RS码生成多项式g(x)如式(10)[12]。 (10) 在码长及本原多项式正确识别后,找到连零码谱出现的位置对应的码根,根据式(7)计算出生成多项式g(x)。 步骤4 按正确的等价码长n′构建分析矩阵,计算每列的0,1概率方差d(i),并与门限值Vth相比较,得到等价信息位长度k′,得到码率为k′/n′。 步骤5 估计符号数m0,并遍历m0次本原多项式pr0,对码序列作GF上的傅里叶变换。当有N组码字作GF上的傅里叶变换,其中h组码组码字变换后具有相同的连零位置且个数相同时,则正确识别出符号数m及本原多项式pr,则n=n′/m,k=n·k′/n′。 步骤6 找到连零码谱出现位置所对应的码根,根据式(10)计算出生成多项式。 为了验证本文所提方法的有效性,分别针对本原RS码以及缩短RS码设计仿真分析实验,编码参数设置如表2所示。利用Matlab随机生成0,1随机序列,然后以表2中编码参数进行编码,并叠加高斯随机噪声,产生误码率为pe的码序列,并用本文所提出的算法对其进行识别。 表2 参数设置 图2、图3分别给出了在对本原RS码序列进行识别时,方差d与等价码长及等价信息位长之间的关系。 图2 本原RS码的等价码长的估计Fig.2 The equivalent code length recognition of the primitive RS code 图3 本原RS码的等价信息位长的估计Fig.3 The equivalent message length recognition of the primitive RS code 由图中可以看出,在等价估计码长mn为21时,方差D出现最大值,故此时等价码长mn识别为21,并且通过方差d与门限值的对比可以看出有9列大于门限值,故可识别出等价信息位长mk为9,通过计算可知,RS码码率为k/n=9/21=3/7。由于符号数m是等价码长mn的约数,又是等价信息位长mk的约数,且m一般取3~8,故符号数m只能为3,并遍历所对应的本原多项式,对码序列作GF上的傅里叶变换。当且仅当m=3,本原多项式为11(十进制表示)时,在连续码根α,α2,α3,α4处码谱为0,将码根带入式(10)得生成多项式为:g(x)=x4+3x3+x2+2x+3,最后通过计算可得n=7,k=3,至此,就完成了对本原RS码的识别。 图4、图5分别给出了在对缩短RS码序列进行识别时,方差d与等价码长及等价信息位长之间的关系由图中可以看出。 图4 缩短RS码的等价码长的估计Fig.4 The equivalent code length recognition of the shorten RS code 图5 缩短RS码的等价信息位长的估计Fig.5 The equivalent message length recognition of the shorten RS code 同理可得,等价码长mn识别为32,等价信息位长mk为16,通过计算可知,RS码码率为k/n=16/32=1/2。由符号数与等价码长和等价信息位长之间的关系可知,符号数m0的估计值为4,8,遍历所对应的本原多项式,对码序列作GF上的傅里叶变换。当且仅当m=4,本原多项式为19(十进制表示)时,在连续码根α,α2,α3,α4处码谱为0,将码根带入式(10)得生成多项式为:g(x)=x4+13x3+12x2+8x+7,最后通过计算可得n=8,k=4,至此,就完成了对缩短RS码的识别。 图6给出了不同码长下,识别正确率与误码率之间的关系,分别取m等于4~8这5种情况下,此时的RS码分别为(15,11)码、(31,11)码、(63,51)码、(127,113)码及(255,223)码。从图中可以看出,码长越大,识别概率越低。在误码率小于0.02时,本文算法对所有码型的识别概率都能达到90%,具有较好的容错能力。 图6 不同码长的RS码识别性能Fig.6 Recognition result of different RS code 图7 不同算法的性能比较Fig.7 Recognition perfor-mance comparison 图7给出了本文方法与文献[4]中基于码重分布法以及文献[5]中基于高斯约当消元法下的识别正确率与系统误码率之间的关系,RS码采用(7,3)编码,从图中可以看出,本文方法要优于文献中的方法,抗误码性能较好。 根据RS码的编码结构和特性,本文提出了一种新的RS码盲识别算法。该算法首先给出了等价二进制码长识别模型,利用信息位与校验位分离法完成对等价码长和等价信息位长的识别,然后通过搜寻连续码根分布对本原多项式和生成多项式进行识别,最后通过计算完成所有参数的识别。仿真结果表明,与传统方法相比,本文方法能在较高误码率下有效完成对本原RS码及缩短RS码的识别,具有良好的抗误码性能。
P(m2=0)+P(m1=0)×P(m2=1)=
a×b+b×a=2ab
P(m2=1)+P(m1=0)×P(m2=0)=
a×a+b×b=a2+b2
[(a2+b2)-0.5]2-(2ab-0.5)=2(a+b)2-
2ab-a-b-[(a+b)4-4a3b-4ab3]=2-2ab-
1-(1-4a3b-4ab3)=2ab(2a2+2b2-1)=
2ab[2a2+2b2-(a+b)2]=2ab(a-b)2
2.2 符号数及本原多项式识别

2.3 生成多项式识别
2.4 算法流程:
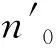
3 仿真实验与性能分析
3.1 实验验证





3.2 识别性能分析


4 结论
