加速度极限值未知条件下的GM-CBMeMBer算法
2019-01-14胡建旺
董 青,胡建旺,吉 兵,张 浩
(1.陆军工程大学石家庄校区,河北 石家庄 050003;2.陆军西安军事代表局驻兰州和乌鲁木齐地区军代室,陕西 西安 710043)
0 引言
真实场景下的目标运动模型是随机变化的,当系统的运动模型与目标匹配时,才能进行有效的目标跟踪。此外,在战场监视中,目标往往是机动的。因此如何建立良好的机动目标运动模型是目标跟踪领域的一个热点问题。近年来,学者专家陆续提出一些运动数学模型如交互式多模型(IMM)[1-2],当前统计 (Current Statistical, CS)模型[3]等。当目标加速度剧烈变化时,CS模型能迅速适应目标运动状态的变化,更精确地跟踪目标且算法计算量较小。文献[4—5]将“当前”统计模型分别与概率假设密度滤波(PHD)算法[6]和多传感器势PHD (CPHD)滤波算法[7]相结合,用以解决多机动目标跟踪问题。文献[8]将“当前”统计自适应模型和高斯混合-势均衡多目标多伯努利[9](GM-CBMeMBer) 滤波算法结合,解决了CBMeMBer算法跟踪机动目标时性能差的问题,但该算法需预先设定加速度极限值。然而在实际场景下,加速度极限值难以准确获取。当目标最大加速度超出预设加速度极限值时,算法跟踪性能较差,稳态误差较大;加速度极限值过小,跟踪滤波器的带宽将减小,稳态误差减小,但对机动目标的跟踪能也会降低。
针对标准CS-GM-CBMeMBer算法对加速度极限值依赖的问题,本文引入协方差自适应递推修正,提出一种加速度极限值未知的GM-CBMeMBer滤波算法。
1 高斯混合势均衡多伯努利滤波器
基于随机有限集[10-11]的CBMeMBer滤波器将目标集当作全局目标,传感器输出的量测作为全局量测。将多目标的状态模型和观测模型表示为随机有限集的形式,将多目标跟踪问题转变为单目标跟踪问题,跳过了量测到航迹的关联问题,极大降低了计算复杂度。利用CBMeMBerF对随机集的概率密度进行近似描述,则可有效地利用随机集理论来解决多目标跟踪问题。下面给出GM-CBMeMBer的滤波过程。
1) 预测
设k-1时刻的多目标密度为:
(1)
则k时刻预测的多目标密度为:
(2)
式(2)中,
(3)
(4)

(5)
(6)
2) 更新
已知k时刻预测的多目标密度描述:
(7)
则其k时刻更新的多目标密度可近似表示为:

(8)
式(8)中,
pD,k为k时刻的目标检测概率,κk(z)为k时刻的杂波强度,Zk为k时刻的量测集合。
2 加速度极限值未知的多机动目标跟踪算法
2.1 问题描述
在惯性坐标系下,CS模型在离散时间系统的状态方程可表示为:
(9)
式(9)中,过程噪声wk-1是服从均值为0,方差为Qk-1的白噪声,上式中的其他参数含义与文献[8]保持一致。其中Qk-1的计算表达式为:
(10)
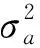
(11)
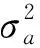
(12)
(13)
目标机动加速度极限值是机动目标性能参数,在跟踪中,通常无法获得。由式(12)、式(13)可知,一旦机动目标的加速度超过人为设置加速度极限值,则跟踪性能会急剧恶化,且当目标加速度较小或为零时,系统方差调整不当,会造成跟踪精度上的损失。
2.2 改进
设定目标加速度极限值的目的在于计算加速度的方差,进而求得过程噪声方差阵。为摆脱算法对加速度极限值的依赖,本文考虑引入自适应卡尔曼滤波算法思想[12],在滤波更新过程中引入式(14)进行协方差自适应递推更新。协方差自适应递推表达式为:
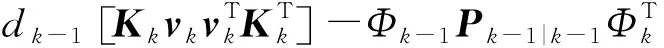
(14)
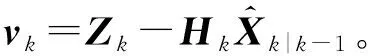
公式(14)对弱、非机动目标具有良好的适应性,但当目标处于快速机动状态或强机动状态时,滤波器稳态误差增大且容易出现跟踪发散现象。因此必须增加算法的鲁棒性,本文采用假设检验判断滤波是否发散,H0表示未出现发散现象,H1表示出现发散现象。检验统计量为:
(15)
(16)
2.3 算法实现步骤
1) 预测
预测的多伯努利随机有限集为:
(17)
2) 假设检验
利用式(15)判断tk,转入式(16)。
3) 更新
更新的多伯努利随机有限集为:

上式各变量可通过本文第1章中计算得出。此外使用式(14)更新过程噪声的方差阵Qk。
4) 剪枝合并
由GM-CBMeMBer递推过程可知,多目标密度的高斯项个数随着时间的推移将无限增加,为控制计算复杂度,需对假设轨迹进行删减、合并操作,剪枝、合并策略参考文献[5]。
5) 状态估计

3 仿真实验
本文针对多机动目标仿真场景进行实验,仿真软件为Matlab 2013b,下面先介绍仿真实验参数,再对仿真结果进行分析。
3.1 仿真参数设置

目标存活概率为pD=0.98,检测概率为pS=0.99,杂波服从λ=20的泊松分布,机动频率a=1/10。
3.2 仿真结果分析
为验证算法有效性,本文采用最优子模式分配(OSPA)距离作为新算法评价准则,其中距离敏感性参数p=1,截断距离c=100。对比算法为文献[11]中所提算法。本仿真真实轨迹如图1。

图1 多目标轨迹图Fig.1 True trajectories of multi-target
图1为多目标真实轨迹图,圆圈表示目标轨迹起点,五角星表示目标轨迹终结。
仿真实验1 设最大加速度amax=30(大于目标真实最大加速度)
由图2可知当目标处于非机动时刻时,改进算法的估计性功能优于标准算法,这是因为标准算法受加速度极限值的影响,处理弱机动和非机动目标能力较差。当目标处于机动时刻,标准算法和改进算法都能较为准确的估计目标。
经过100次蒙特卡罗仿真,目标个数估计如图3所示,改进算法的错估次数为18,标准算法的错估次数为26。由于滤波算法自身的局限性,两种算法在新目标进入监测区域时(1 s,10 s,20 s,60 s左右),存在动态时延现象,产生目标数目低估现象。相比标准算法而言,改进算法的数目估计精度稍有提高。
在30~40 s左右,目标机动性较强,由图4可知,两种算法OSPA距离相近,表示在目标强机动时,跟踪性能相近。在50~80 s左右,目标多处于匀速运动状态,机动性较弱,改进算法的OSPA距离小于标准算法,即改进的滤波器的稳态误差更低。
仿真实验2 设最大加速度amax=10(小于目标真实最大加速度)

图2 仿真1的多目标位置估计Fig.2 Multi-target position estimate of Simulation 1

图3 仿真1的目标数目估计Fig.3 Target number estimate of Simulation 1
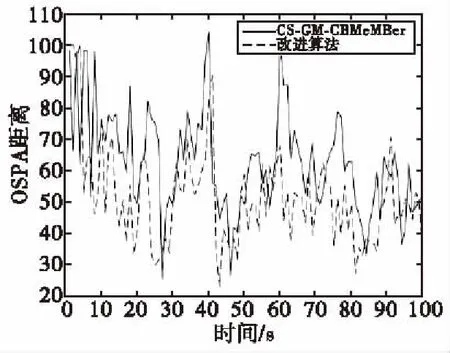
图4 仿真1的多目标跟踪误差Fig.4 Multi-target tracking error of Simulation 1
对比图2、图5可以看出,在x轴方向,在目标运动时间内,当加速度极限值小于目标真实最大加速度时(18~27 s内),标准算法的位置估计的偏离度更大,由于之前时刻的估计精度不高,致使后续弱机动时刻,状态估计精度仍然较低;在28~38 s内,y轴方向的状态估计误差增大。当目标处于弱机动时刻,改进算法通过协方差匹配自适应卡尔曼滤波算法,可以准确地获取状态噪声协方差,得到良好的状态估计,当目标处于强机动时刻,不受加速度极限值的控制,相比标准算法,具有更好的状态估计性能。

图5 仿真2的多目标位置估计Fig.5 Multi-target position estimate of Simulation 2
由图6可知,仿真条件2下标准算法的数目估计准确度极大降低,100 s的仿真时间内,错估次数在40次左右,而改进算法的数目估计精度等同于仿真条件1下的估计精度。
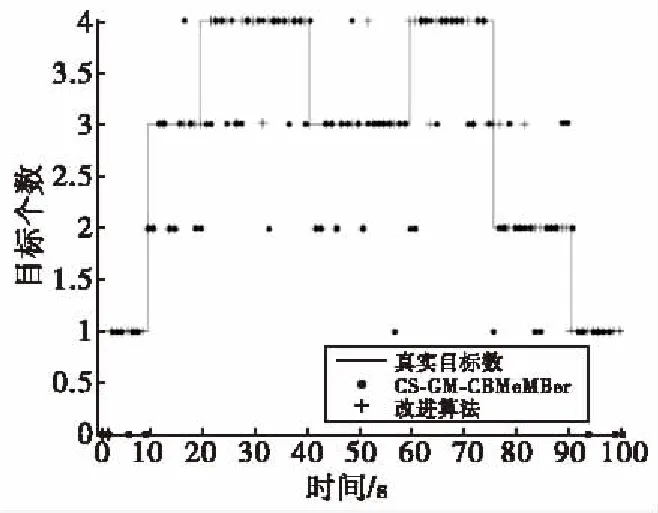
图6 仿真2的目标数目估计Fig.6 Target number estimate of Simulation 2
由图7可知,当预设的加速度极限值小于目标真实加速度时,标准算法的稳态误差增大。改进算法的OSPA距离明显低于标准算法,表明改进算法稳定性高于标准算法。但在算法起始时刻,改进算法的误差峰值仍然较大,下一步将研究性能更优的自适应滤波算法。
仿真实验1中将标准算法的加速度极限值参数化,改进算法和标准算法跟踪性能相当,但改进算法具有更高的稳定性。仿真实验2中,若标准算法加速度预设不准确,则估计精度和算法稳定性都会极大降低,而改进算法不受加速度极限值的影响,能保持较好的估计性能。

图7 仿真2的多目标跟踪误差Fig.7 Multi-target tracking error of Simulation 2
4 结论
本文提出了加速度极限值未知条件下的GM-CBMeMBer算法。该算法基于GM-CBMeMBer算法,建立了协方差自适应递推式,以此摆脱需要预设加速度极限值的限制;为防止滤波发散,建立检验统计量表达式,设置方差阵修正系数,对协方差阵进行修正。仿真结果表明,与标准CS-GM-CBMeMBer算法相比,在加速度极限值不精确或无法获得的条件下,改进算法具有更好的跟踪精度和稳定性,更适用于真实场景下的多机动目标跟踪。本文实现了对加速度极限值的自适应,下一步将研究机动频率和加速度极限值双重自适应跟踪算法。
