火炮身管指向测试方法研究
2019-01-14谢杰涛李海洋吴红权
谢杰涛,马 威,吴 娟,李海洋,吴红权
(中国白城兵器试验中心,吉林 白城 137001)
0 引言
火炮身管指向是影响火炮射击准确度的关键因素,火炮瞄准精度、调炮精度、复瞄精度等指标的测试本质上都是通过对火炮身管指向的测量完成的。
火炮身管指向的测试方法很多,文献[1]总结了CCD+坐标靶、CCD+电光源、激光器+PSD和激光陀螺等多种方法,这些方法的主要问题是需要在火炮身管上加装测试设备,可能会影响武器系统状态。双经纬仪交汇方法是主要的非接触测量方法,但传统的双经纬仪交汇方法在不同的布展方案下有不同的测试结果,文献[2-6]从不同角度寻求优化的布站方案,但是都没有给出不同方案下测试精度的量化结果,更没有经过大量工程实践的检验。本文对测试误差进行研究,解决了传统双经纬仪交汇方法测试结果不一致的问题,不但能计算给定布站方案的测试精度,而且能给出满足测试精度的布站方案,在多个型号武器系统试验中取得了良好的效果。
1 测试模型
采用双经纬仪交汇法进行测量,其工作原理为利用两台经纬仪与代表火炮身管轴线的两个标记点建立空间坐标系,通过两个经纬仪分别观瞄两个标记点获得一组所需数据,经结算可得到火炮身管首尾标记点连线与经纬仪基线夹角。引入真北后,可标定出经纬仪基线的北向角,经几何关系推导获得火炮身管轴线空间指向。
1.1 方位角测试模型
如图1所示,火炮位于水平面上,在火炮身管前后两端(距离尽量远)各贴一个十字标a和b,要求线ab与火炮身管轴线平行;架设经纬仪A、B,以AB连线为经纬仪的基线,调平对瞄建立坐标系;C、D点分别是a和b点在基线AB上的垂直投影,c点为 a点在线 bD 上的投影。设∠aAC=α1,∠bAD=α2,∠aBC=β1,∠bBD=β2,∠bac=α,aC=H1,bD=H2,AB=L,AC=L1,DB=L2。其中α即为经纬仪基线与火炮身管轴线在水平面上的方位夹角。α1,α2分别是经纬仪A测量得到的a和b相对于基线AB的水平角;β1,β2分别是经纬仪B测量得到a和b相对于基线AB的水平角。
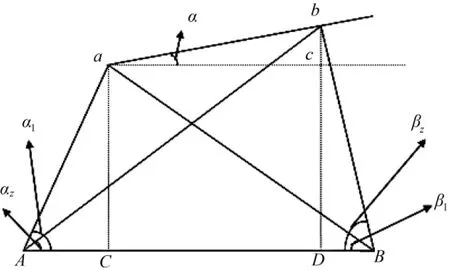
图1 方位角测试原理图
已知:α1,α2,β1,β2,求 α。

通过等式变换可得:

由式(1)可知,只要测出 α1、α2、β1、β24 个角度值就可得到炮管轴线与双经纬仪基线在水平面上的方位夹角α。因此,测量调炮前后的α角,求差即为自动调炮方位角的测试结果。
1.2 高低角测试模型
如图2所示,C,D分别为a和b在通过基线AB的水平面上的垂直投影点;∠CAB=α1,∠DAB=α2,∠CBA=β1,∠DBA=β2,∠aAC=γ1,∠bAD=γ2,∠bac=ε,AC=a,AD=b,AB=d,CD=c,aC=h1,bD=h2。其中 ε为火炮身管轴线与大地水平面之间的高低夹角。α1,α2分别是经纬仪A测量得到的a和b相对于基线AB的水平角;β1,β2分别是经纬仪B测量得到a和b相对于基线AB的水平角;γ1,γ2分别为经纬仪A测量得到a和b相对于水平面的垂直角度。
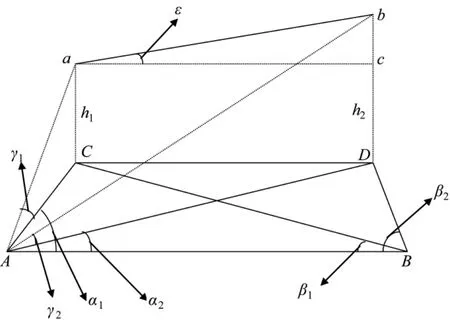
图2 高低角测试原理图
已知:α1,α2,β1,β2,γ1,γ2,求 ε。
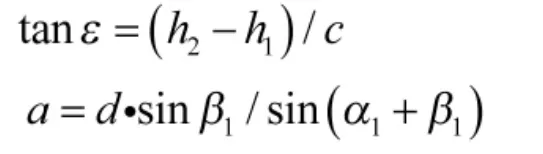

通过等式变换可得:

由式(2)可知,只要测出 α1、α2、β1、β2、γ1、γ26 个角度值就可得到炮管轴线与大地水平面之间的高低夹角ε。
2 误差分析
双经纬仪交汇法的测量精度主要受经纬仪测角误差、计算误差及布站误差等因素影响(绝对角度测量还包括,方位基准角引入误差)。
2.1 经纬仪测角误差
经纬仪测角误差按其成因可划分为瞄准误差和仪器误差。其中,瞄准误差在正常操作使用情况下,由经纬仪瞄准方式及望远镜放大倍率决定。例如,采用压线法、放大倍率30的经纬仪瞄准误差一般为2.5"。仪器误差主要由3部分组成:三轴误差(视准轴、水平轴、垂直轴)、偏心误差及分划误差。经纬仪的三轴(视准轴、水平轴、垂直轴)之间在测角时应满足视准轴与水平轴正交,水平轴与垂直轴正交,垂直轴与点位铅垂线一致。当这些关系不能满足时,将分别引起视准轴误差、水平轴倾斜误差、垂直轴倾斜误差。偏心误差和水平分度盘分划误差,主要由经纬仪的生产加工工艺决定。经纬仪安装过程要求三心一致(照准部旋转中心、分度盘分划中心及分度盘回转中心)。安装精度决定了偏心误差大小,主要包括照准部偏心误差及水平分度盘偏心误差。经纬仪水平角测量值,是通过水平分度盘上的分划读数得到的,分度盘加工精度决定了水平分度盘分划误差大小,一般可分为3种:分划偶然误差、分度盘分划长周期误差、分度盘分划短周期误差。双经纬仪交汇法测量过程中,通常采用单次架设7次测量的方式。此时,瞄准误差为随机误差,三轴误差、偏心误差及分划误差为系统误差。
2.2 方位角误差计算
分别求 α 对 α1、α2、β1、β2的偏导,结果如下:
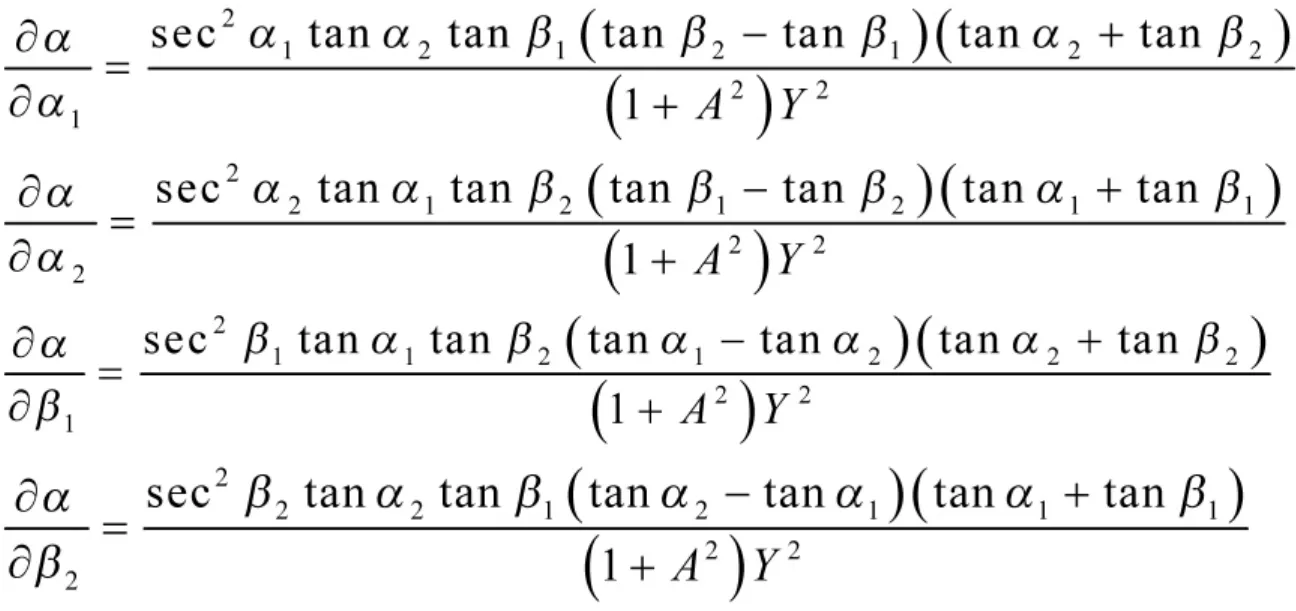
将上述结果代入误差传递公式:

其中 σα1、σα2、σβ1、σβ2均取 δ=0.011 6 mil,简化后得方位角传递误差:

2.3 高低角误差计算
分别求 ε 对 α1、α2、β1、β2、γ1、γ2的偏导,结果如下:
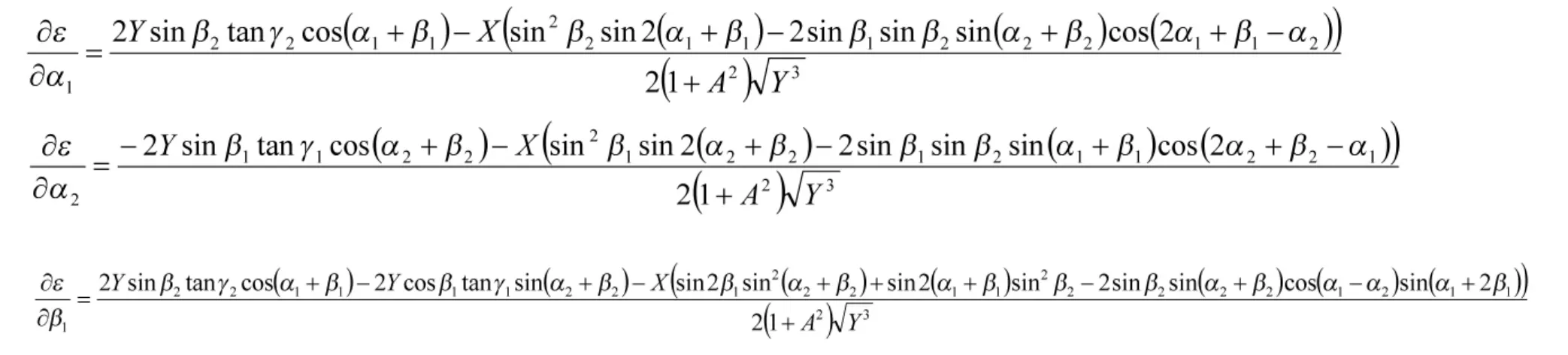

将上述结果代入下式:


2.4 布站误差分析
在不同的点位架设经纬仪进行测试,其误差大小是不同的,这是造成测试结果不一致的主要原因。为确定经纬仪保精度布站位置,需建立经纬仪位置与 α1、α2、β1、β2、γ1、γ2的解析关系,并依此推算出经纬仪观测值,计算经纬仪在不同位置的测试误差。如图3所示:设两经纬仪基线AB距离为y,炮管两十字线ab距离为pl,经纬仪基线与炮管距离为x,炮管尾端十字线与经纬仪高度差为h,z为扫描移动步长。建立如下关系表达式:



图3 经纬仪位置与瞄准角解析关系图
3 实验验证
3.1 模拟实验
3.1.1 模拟炮管实验设计
1)模拟炮管适当位置粘贴2组十字标,使具备模拟2.5 m(普通火箭炮身管长度)、4 m(普通自行加榴炮身管长度)火炮身管调炮精度测试的条件;
2)将方位精准快组合件安装在三轴数控转台上,调节安装位置确保基准镜法线与转台基准面平行;
3)将模拟炮管刚性安装在转台台面上,调节安装位置使炮管轴线与转台基准面平行,与基准镜法线正交;
4)在室内方位基准座上安装方位基准棱镜组件,架设自准直经纬仪,为系统建立测量基准如图5所示。
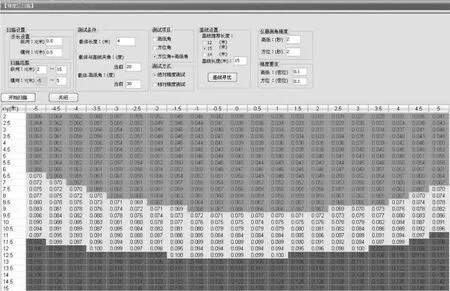
图4 利用蒙特卡罗方法扫描不同测试区域的精度分布情况图
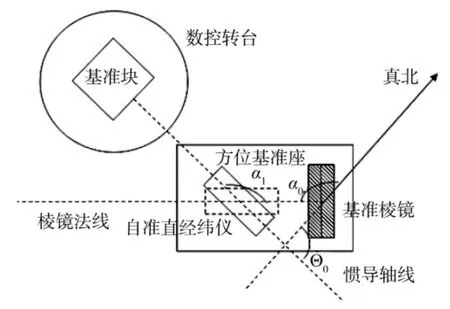
图5 基准建立示意图
5)在选定位置架设经伟仪,调平对准,使两经纬仪光轴在同一直线上,然后将两经纬仪读数置零,经纬仪布站方案如图6所示:

图6 经纬仪布站方案
6)两个经纬仪分别观瞄炮管上两个十字标中心点,测得 4 个方位角 α1、α2、β1、β2和 2 个高低角;
7)采集上述数据,进行处理计算,输出计算结果。
(3)二叠系。测区二叠系发育齐全,出露较好,分布于东部鹧鸪江湘桂铁路以南—三门江林场、六座—大塘口—河表—通天岩一带及北部柳城凤山一带,面积约52.93 km2,约占测区面积的6.2%。二叠系除马平组上部属下统外,以上的地层划分为中统、上统,五个组,八个段。
3.1.2 标杆法实验设计
1)在室外开阔场地内适当位置,架设陀螺仪经纬仪及标杆,调整标杆架设位置及高度,使两标记点可同时处于陀螺仪经纬仪主光轴上;
2)记录陀螺仪经纬仪测量出的标记点连线与真北夹角及标记点连线俯仰角,作为测试真值;
3)根据标记点连线长度及空间位置等信息,计算出场内各点位炮管指向精度测试系统理论测量精度;
4)在选定位置架设自准直经伟仪,调平对准,使两经纬仪光轴在同一直线上,然后将两经纬仪读数置零,现场各仪器布站方案如下页图7所示;
5)陀螺仪经纬仪与自准直经纬仪A对瞄,并记录陀螺仪经纬仪与自准直经纬仪A读数,计算得到两台自准直经纬仪基线与真北夹角;
6)两个经纬仪分别观瞄两标记点,测得4个方位角 α1、α2、β1、β2和 2 个高低角 γ1、γ2;
7)采集上述数据进行处理,系统自动计算得出标记点连线与真北夹角及标记点连线俯仰角,记录系统测量结果;
8)重复步骤6)、7)过程7次,统计均方差。
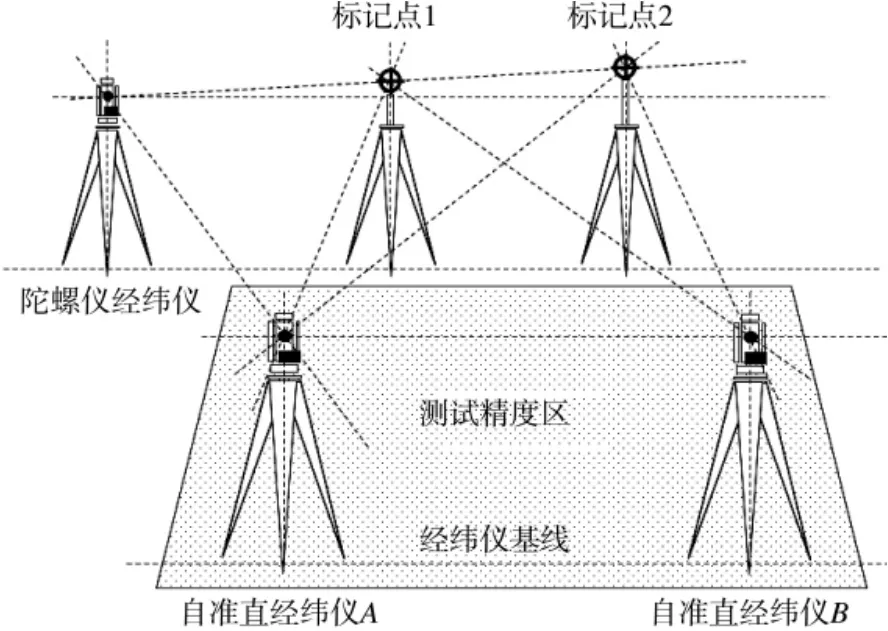
图7 标杆法经纬仪布站方案
3.1.3 实验结果分析
实测结果与理论计算结果详见表1、表2。结果表明实际测量误差与理论计算误差基本吻合,反映了经纬仪测角误差分析正确,不能将经纬仪自身误差2′简单带入误差传递模型;证明了测试计算模型、扫描模型、基线寻优算法正确;实测精度区划定合理。
3.2 实装测试
在某型火箭炮常温最大射程地面准确度试验中,该系统测量了射击前身管实际空间指向。使用过程中,体现了本方法准确、快捷、架设方便等优点,确保了试验的顺利实施。测试数据如表3所示(表中数据已进行脱密处理)。
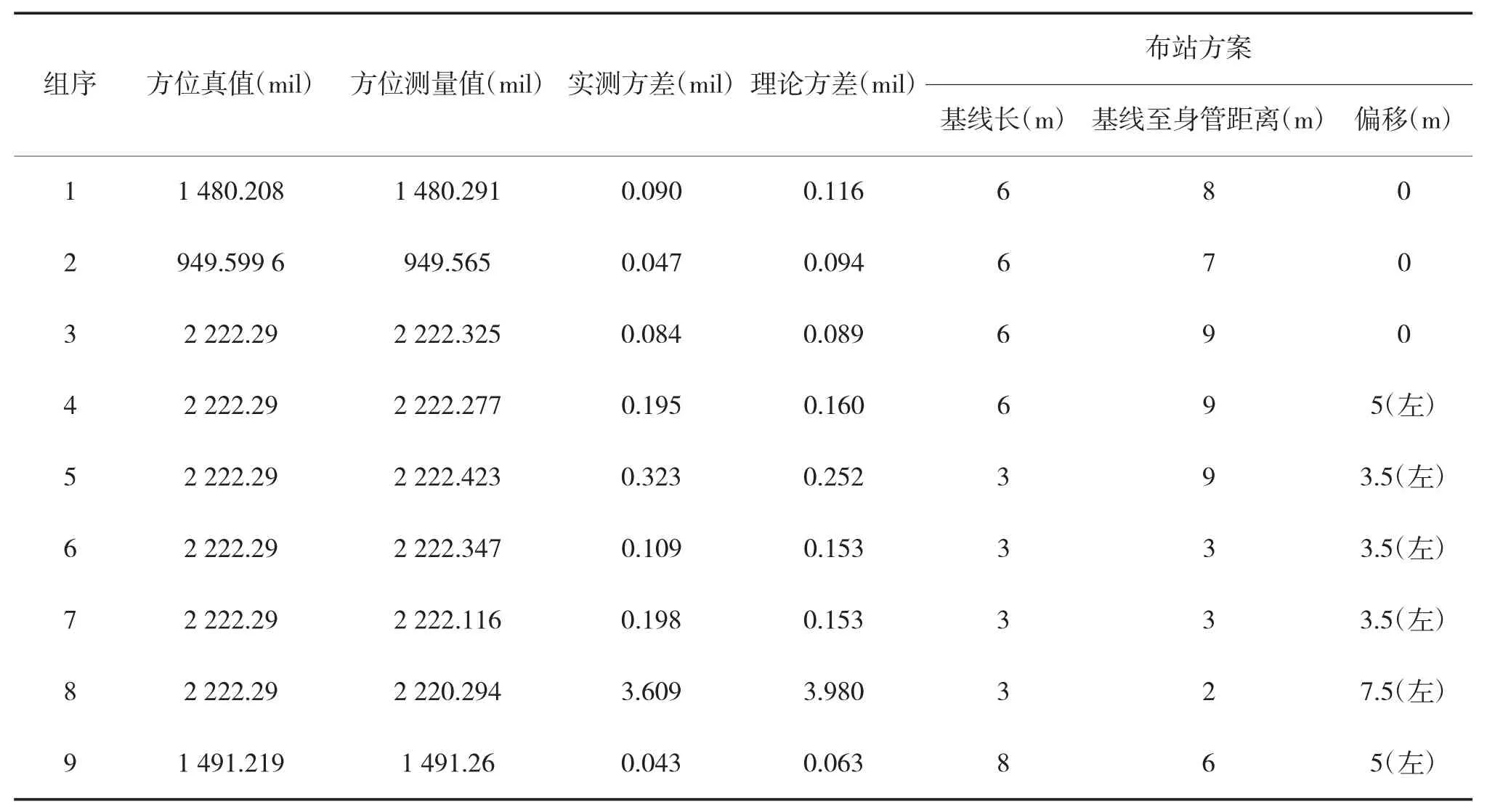
表1 模拟炮管测试结果对比分析表

表2 标杆法测试结果对比分析表

表3 实际应用数据对比分析表
4 结论
本文针对高精度火炮身管指向测量中测试结果不一致的问题,在经典的双经纬仪交汇方法的基础上,对测试误差进行了分析,推导了误差计算模型,进而采用蒙特卡罗方法计算不同测试点位的误差大小,保证了测试结果的一致性,为高精度测试火炮身管指向提供了依据,在多个型号武器系统试验中取得了良好的效果。
